Пропорции в математике как решать 6 класс

Узнайте, как решать задачи на пропорции в математике для учеников 6 класса. Научитесь использовать пропорции для нахождения неизвестных значений и решения практических задач.

Пропорции — это одна из основных тем, которую изучают в школьной математике. Решение задач на пропорции помогает развивать навыки анализа и логического мышления у учеников. В 6 классе ученики начинают изучать эту тему более подробно и применять ее для решения различных практических задач.

Для решения задач на пропорции необходимо освоить несколько шагов. Во-первых, нужно понять, что такое пропорция. Пропорция — это равенство двух отношений. То есть, в пропорции имеется четыре числа, и отношение первых двух чисел равно отношению последних двух чисел. В 6 классе ученики обычно работают с пропорциями, где неизвестным является одно из четырех чисел.

Во-вторых, для решения задач на пропорции необходимо научиться составлять уравнения. Уравнение для пропорции может быть записано в форме a:b = c:d, где a, b, c, d — числа из условия задачи. Для нахождения неизвестного числа, нужно решить это уравнение. Один из способов — перекрестное умножение: a * d = b * c. Затем, если необходимо найти значение неизвестного числа, можно применить правило трех, разделив результат перекрестного умножения на известное число.

Пропорции — это увлекательная и полезная тема, которая помогает развивать навыки логического мышления и применять математические знания для решения практических задач. С помощью пошагового руководства вы сможете научиться решать задачи на пропорции в 6 классе и успешно справляться с ними в дальнейшем.

Понятие и примеры пропорции

Пропорция может использоваться для решения различных задач. Например, если нам известно, что 5 яблок стоят 10 рублей, то мы можем использовать пропорцию для определения стоимости определенного количества яблок. Пусть мы хотим узнать, сколько стоят 3 яблока. Подставим значения в формулу пропорции:

• a = 5 (количество яблок)
• b = 10 (стоимость)
• c = 3 (количество яблок, которое мы хотим узнать стоимость)
• d (стоимость, которую мы хотим найти)

Теперь мы можем записать пропорцию и решить ее:

5:10 = 3:d

Мы можем упростить эту пропорцию, поделив обе стороны на 5:

1:2 = 3:d

Теперь мы можем найти значение d, умножив обе стороны на 2:

2 = 3:d

Значит, 3 яблока стоят 2 рубля.

Таким образом, пропорция позволяет нам решать задачи, связанные с соотношением различных величин.

Типичные задачи на пропорции в 6 классе

В шестом классе при изучении пропорций в математике студенты решают различные типы задач. Ниже приведены некоторые типичные задачи, которые могут встретиться в учебнике или на уроке.

1. Задачи, связанные с расчетом отношений. Например, студентам может быть дано задание посчитать, сколько бутылок вмещается в коробку, если известно, что в одной коробке помещается 10 бутылок.
2. Задачи на нахождение неизвестной величины. В этом типе задач студентам может быть предложено найти неизвестное значение, если известны другие значения в пропорции. Например, если известно, что 3 яблока стоят 15 рублей, студентам нужно найти стоимость одного яблока.
3. Задачи на сравнение пропорций. Этот тип задач позволяет студентам сравнивать различные пропорции и находить более выгодное решение. Например, студентам может быть предложено сравнить стоимость яблок в разных магазинах, их вес и количество.
4. Задачи на пропорциональное увеличение или уменьшение. В таких задачах студентам может быть предложено умножить или разделить значения в пропорции, чтобы получить новые значения. Например, если известно, что 2 яблока стоят 10 рублей, студенты могут быть попрошены найти стоимость 5 яблок.

Это лишь некоторые примеры задач, которые могут встретиться в 6 классе при изучении пропорций. Важно понимать основные принципы решения задач на пропорции и использовать их для решения различных задач в математике.

Шаг 1: Определение неизвестного значения

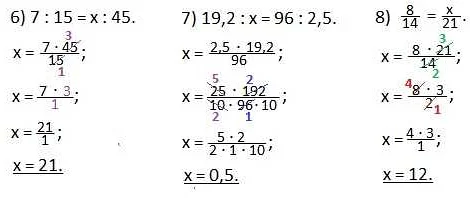
Чтобы определить неизвестное значение, нужно внимательно прочитать условие задачи и выделить информацию о двух известных величинах. Затем необходимо использовать пропорцию, которая устанавливает соотношение между этими величинами.

Например, в задаче может быть дано, что 3 яблока стоят 60 рублей, и нужно найти стоимость 5 яблок. В данном случае известными значениями являются количество яблок (3) и их стоимость (60 рублей), а неизвестным значением является стоимость 5 яблок. С помощью пропорции можно выразить соотношение между количеством яблок и их стоимостью, и найти неизвестное значение.

Важно помнить, что при определении неизвестного значения нужно действовать пошагово и внимательно анализировать информацию в задаче. Это поможет правильно построить пропорцию и получить верный результат.

Шаг 2: Поставить пропорцию

Чтобы поставить пропорцию, мы используем следующую формулу:

известное значение 1 / известное значение 2 = неизвестное значение 1 / неизвестное значение 2

Здесь «известное значение 1» и «известное значение 2» — это значения, которые уже известны нам из задачи. «Неизвестное значение 1» и «неизвестное значение 2» — это те значения, которые мы хотим найти.

Поставив пропорцию, мы получаем уравнение, которое мы можем решить для нахождения неизвестных значений. Для этого мы можем использовать перекрестное умножение: умножаем «известное значение 1» на «неизвестное значение 2» и «известное значение 2» на «неизвестное значение 1». Затем сравниваем полученные значения и находим неизвестные значения.

Поставление пропорции является важным шагом в решении задач на пропорции, поскольку позволяет нам перейти от словесного описания задачи к математическому уравнению. Таким образом, мы можем использовать математические методы для решения задачи и нахождения неизвестных значений.

Шаг 3: Нахождение пропорционального значения

После того, как мы установили пропорцию и выразили ее в виде уравнения, мы можем перейти к нахождению пропорционального значения. Для этого нам понадобится решить уравнение.

Пропорция представляет собой равенство двух отношений. Чтобы найти неизвестное значение, мы можем использовать свойство равенства отношений. Достаточно перекрестно умножить числа в пропорции.

Например, если у нас есть пропорция: a/b = c/d, то чтобы найти значение неизвестной величины, мы можем умножить a на d и b на c. Таким образом, получится уравнение: a*d = b*c.

Решаем это уравнение и находим значение неизвестной величины.

Важно помнить, что если пропорция содержит несколько неизвестных величин, то мы должны знать значения хотя бы одной из них, чтобы решить уравнение.

Итак, нахождение пропорционального значения требует решения уравнения, полученного из пропорции перекрестным умножением чисел. Этот шаг поможет нам найти значение искомой величины в задаче.

Шаг 4: Проверка решения

После того как вы нашли решение задачи на пропорции, очень важно проверить его правильность. Это поможет вам убедиться, что вы не допустили ошибок во время решения. Вот несколько шагов, которые помогут вам проверить ваше решение:

1. Проверьте правильность вычислений. Перепроверьте все математические операции, которые вы выполнили в ходе решения задачи. Убедитесь, что вы правильно умножили, разделили, сложили и вычли все числа.

2. Подставьте полученные значения в исходную задачу. Возьмите полученные значения и подставьте их в исходную задачу. Убедитесь, что равенства выполняются и что полученные значения удовлетворяют условию задачи.

3. Прочтите задачу еще раз. Перечитайте условие задачи, чтобы убедиться, что вы правильно поняли все требования и ограничения. Убедитесь, что ваше решение соответствует задаче.

Если ваше решение проходит все эти проверки, значит вы правильно решили задачу на пропорции. Если же ваше решение не проходит проверку, вернитесь к предыдущим шагам и перепроверьте свои вычисления и логику решения.

Дополнительные советы и подсказки

Чтобы успешно решать задачи на пропорции в математике в 6 классе, можно использовать следующие советы и подсказки:

1. Понимание пропорций: Прежде чем приступить к решению задач, необходимо хорошо понимать, что такое пропорция и как она работает. Пропорция — это равенство двух отношений, где одно отношение равно другому. Зная эту основу, можно легче справляться с задачами.

2. Правильная запись пропорций: Важно правильно записывать пропорции, чтобы не запутаться и избежать ошибок. Обычно пропорции записывают в виде a:b = c:d, где a, b, c, d — числа или выражения.

3. Использование обратной пропорции: Если в задаче указана обратная пропорция, то можно применить к ней следующее правило: умножение чисел, составляющих одно отношение, должно давать одно и то же произведение, как и у другого отношения. Например, в задаче про расстояние и время, если одно расстояние увеличивается, то время уменьшается, и наоборот.

4. Использование дополнительных величин: Иногда в задаче нужно найти неизвестное значение, которое не указано явно. В таких случаях можно ввести дополнительную величину, условно обозначив ее буквой, и построить пропорцию с использованием этой величины. Затем можно решить получившуюся пропорцию и найти искомое значение.

5. Проверка решения: После решения задачи важно всегда проверять полученный ответ. Для этого можно подставить найденные значения обратно в исходную пропорцию и проверить, сходятся ли они.

Следуя этим советам и подсказкам, вы сможете более уверенно и эффективно решать задачи на пропорции в математике в 6 классе.

Примеры решения задач на пропорции

Решение задач на пропорции в математике может быть довольно простым, если вы знакомы с основными правилами и принципами работы с пропорциями. В этом разделе мы рассмотрим несколько примеров задач и пошагово разберем, как их решать.

Пример 1:

Если 5 яблок стоят 200 рублей, то сколько будет стоить 8 яблок?

Для решения этой задачи воспользуемся пропорцией:

5	:	200
8	:	?

Перепишем пропорцию в виде уравнения:

5 / 200 = 8 / x

Теперь решим полученное уравнение. Умножим обе стороны на x:

5x = 8 * 200

Разделим обе стороны на 5:

x = 8 * 200 / 5

x = 320

Таким образом, 8 яблок будут стоить 320 рублей.

Пример 2:

Если 4 ручки стоят 120 рублей, то сколько будет стоить 10 ручек?

Для решения этой задачи воспользуемся пропорцией:

4	:	120
10	:	?

Перепишем пропорцию в виде уравнения:

4 / 120 = 10 / x

Теперь решим полученное уравнение. Умножим обе стороны на x:

4x = 10 * 120

Разделим обе стороны на 4:

x = 10 * 120 / 4

x = 300

Таким образом, 10 ручек будут стоить 300 рублей.

Приведенные примеры показывают, что решение задач на пропорции сводится к установлению соотношения между величинами и последующему решению полученной пропорции. Будьте внимательны при записи и решении пропорций, чтобы избежать ошибок и получить правильный ответ.

Вопрос-ответ:

Как решить задачу на пропорцию с одним неизвестным числом?

Для решения задачи на пропорцию с одним неизвестным числом нужно записать пропорцию и выразить неизвестное число. Затем провести вычисления и найти его значение.

Какие шаги необходимо выполнить для решения задачи на пропорцию с двумя неизвестными числами?

Для решения задачи на пропорцию с двумя неизвестными числами нужно записать пропорцию, затем составить систему уравнений и решить ее с помощью метода подстановки или метода сложения.

Как определить, является ли пропорция прямой или обратной?

Пропорция является прямой, если при увеличении значений одной величины, значения другой величины также увеличиваются. Пропорция является обратной, если при увеличении значений одной величины, значения другой величины уменьшаются.

Можно ли использовать пропорции для решения задач на проценты?

Да, пропорции можно использовать для решения задач на проценты. Например, если нужно найти процент от числа, можно составить пропорцию и найти значение процента.

Как применить пропорцию для решения задачи на доли и десятичные дроби?

Для решения задачи на доли и десятичные дроби с использованием пропорции, нужно записать пропорцию, в которой одна доля или десятичная дробь будет соответствовать другой доле или десятичной дроби. Затем нужно провести вычисления и найти значение неизвестной доли или десятичной дроби.

Как решить задачу на пропорцию в математике в 6 классе?

Для решения задачи на пропорцию в 6 классе, необходимо сначала определить, какие величины являются пропорциональными. Затем можно составить пропорцию и решить ее, используя свойства пропорций. Например, если задача требует найти значение одной величины, когда известно значение другой величины и пропорция между ними, можно использовать правило трех или кросс-метод. Важно помнить, что при решении задач на пропорцию необходимо внимательно анализировать условие задачи и правильно интерпретировать данные.

Видео по теме: