Математика 6 класс мерзляк дроби как решать
Содержимое
- 1 Математика 6 класс мерзляк дроби как решать
- 1.1 Основные понятия дробей
- 1.2 Сложение и вычитание дробей
- 1.3 Умножение дробей
- 1.4 Деление дробей
- 1.5 Приведение дробей к общему знаменателю
- 1.6 Решение задач на дроби с помощью уравнений
- 1.7 Проценты и дроби
- 1.8 Практические задачи по дробям
- 1.9 Вопрос-ответ:
- 1.9.0.1 Как решать задачу, где нужно сложить две дроби?
- 1.9.0.2 Как упростить дробь в задаче?
- 1.9.0.3 Как решить задачу, где нужно вычесть одну дробь из другой?
- 1.9.0.4 Как решить задачу, где нужно умножить две дроби?
- 1.9.0.5 Какие принципы стоит учитывать при решении задач по дробям в 6 классе?
- 1.9.0.6 Какие методы можно использовать при решении задач на сложение и вычитание дробей в 6 классе?
- 1.9.0.7 Как решить задачу по умножению дробей в 6 классе?
- 1.10 Видео по теме:
Узнайте, как решать задачи по дробям в 6 классе по математике по методике Мерзляка. Научитесь сокращать дроби, складывать и вычитать их, умножать и делить, а также решать уравнения с дробями. Полезные советы и примеры решения задач.
Работа с дробями – одна из важных тем в математике для учащихся 6 класса. Понимание основных правил и навыков работы с дробями поможет решать разнообразные задачи, связанные с этой темой. В учебнике Мерзляк представлены подробные объяснения и примеры, которые помогут разобраться в этой математической области.
Перед тем как приступить к решению задач по дробям, необходимо освоить основные понятия. Дробь состоит из числителя и знаменателя, которые разделяются горизонтальной чертой. Числитель – это число, которое находится над чертой, и показывает, сколько частей мы берем. Знаменатель – это число, которое находится под чертой, и показывает, на сколько частей целого мы делим.
Например, если мы имеем дробь 3/4, то это означает, что мы берем 3 части из 4-х возможных.
Для того чтобы решать задачи по дробям, необходимо научиться сравнивать дроби между собой, выполнять арифметические операции с дробями (сложение, вычитание, умножение, деление) и упрощать дроби. В учебнике Мерзляк подробно рассматриваются все эти аспекты, приводятся примеры, а также предлагаются задачи, которые помогут закрепить полученные знания.
Умение решать задачи по дробям является не только важным навыком в математике, но также находит свое применение в повседневной жизни. Например, при делении пиццы или торта на части, при расчете времени и дистанции, при работе с финансами и многих других ситуациях. Поэтому освоение этой темы является важным этапом в обучении математике 6 класса.
Основные понятия дробей
Числитель и знаменатель могут быть как целыми числами, так и десятичными дробями. Например, дроби 3/4, 5/8, 1/2 представляют собой отношение целых чисел, а дроби 0,5/2, 0,75/4 – отношение десятичных дробей.
Основные операции с дробями включают сложение, вычитание, умножение и деление. Для выполнения этих операций необходимо привести дроби к общему знаменателю. При сложении и вычитании дробей, числители складываются или вычитаются, а знаменатель остается неизменным. При умножении дробей, числитель одной дроби умножается на числитель другой дроби, а знаменатель одной дроби умножается на знаменатель другой дроби. При делении дробей, числитель одной дроби умножается на знаменатель другой дроби, а знаменатель одной дроби умножается на числитель другой дроби.
Дроби могут быть представлены на числовой прямой или в виде десятичных дробей. На числовой прямой, дробь представляет собой точку между двумя целыми числами. Десятичные дроби представляют собой десятичную запись дроби, где знаменатель является степенью десяти, например, 0,5 или 0,75.
Знание основных понятий о дробях позволяет ученикам успешно решать задачи по дробям и применять их в реальной жизни, например, при расчете долей, сравнении цен и долей, и в других ситуациях.
Сложение и вычитание дробей
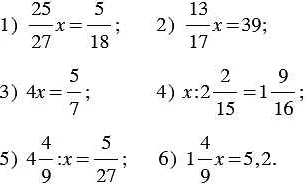
Чтобы сложить или вычесть дроби, нужно, прежде всего, привести их к общему знаменателю. Общий знаменатель – это число, на которое делятся все знаменатели в данных дробях.
Для сложения дробей с одинаковыми знаменателями, нужно просто сложить их числители и записать полученную сумму над общим знаменателем.
Например, чтобы сложить дроби 1/4 и 2/4, нужно сложить числители 1 и 2, получив 3, и записать результат над общим знаменателем 4: 3/4.
Если дроби имеют разные знаменатели, их необходимо привести к общему знаменателю. Для этого следует найти наименьшее общее кратное (НОК) знаменателей и заменить каждую дробь на эквивалентную ей дробь с новым знаменателем.
Например, чтобы сложить дроби 1/3 и 1/6, нужно найти НОК знаменателей 3 и 6, равный 6. Затем, умножив числитель и знаменатель первой дроби на 2 (чтобы получить знаменатель 6), и второй дроби на 1 (чтобы сохранить ее значение), мы получим: 2/6 и 1/6. Затем, просто сложив числители, получаем 3/6 или 1/2.
Вычитание дробей выполняется аналогичным образом. Если знаменатели дробей одинаковые, нужно просто вычесть числители и записать полученную разность над общим знаменателем.
Если знаменатели разные, необходимо привести дроби к общему знаменателю и вычесть числители.
Например, чтобы вычесть дробь 2/5 из дроби 7/10, нужно найти НОК знаменателей 5 и 10, равный 10. Затем, умножив числитель и знаменатель первой дроби на 2 (чтобы получить знаменатель 10), и второй дроби на 1 (чтобы сохранить ее значение), мы получим: 4/10 и 7/10. Затем, вычитая числители, получаем 3/10.
Таким образом, сложение и вычитание дробей – это важные навыки, необходимые для успешного решения задач по дробям в математике 6 класса.
Умножение дробей
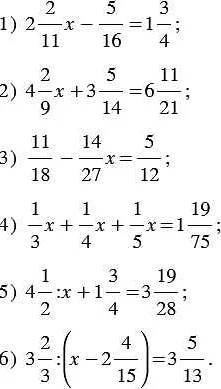
Для умножения дробей необходимо выполнить следующие шаги:
- Умножить числитель одной дроби на числитель другой дроби.
- Умножить знаменатель одной дроби на знаменатель другой дроби.
- Полученные результаты записать в виде дроби, где числитель — результат умножения числителей, а знаменатель — результат умножения знаменателей.
- Дробь можно сократить, если числитель и знаменатель имеют общие делители.
Пример умножения дробей:
Дробь 1Дробь 2Результат
| 2/3 | 4/5 | (2 * 4) / (3 * 5) = 8/15 |
В данном примере, числитель дроби 1 (2) умножается на числитель дроби 2 (4), а знаменатель дроби 1 (3) умножается на знаменатель дроби 2 (5). После умножения получаем результат — дробь 8/15.
Если числитель и знаменатель дроби имеют общие делители, например 8/16, то дробь можно сократить. В данном случае, оба числа делятся на 8, поэтому дробь можно сократить до 1/2.
Деление дробей

- Инвертировать делитель (дробь, на которую делим), поменяв местами числитель и знаменатель.
- Умножить делимое (дробь, которую делим) на инвертированный делитель.
- Сократить полученную дробь, если это возможно.
Пример:
Дано: $\frac{3}{4} \div \frac{2}{5}$
- Инвертируем делитель: $\frac{3}{4} \div \frac{5}{2}$
- Умножаем делимое на инвертированный делитель: $\frac{3}{4} \cdot \frac{5}{2} = \frac{15}{8}$
- Сокращаем полученную дробь: $\frac{15}{8} = \frac{15}{2} \div \frac{8}{2} = \frac{15}{2} \cdot \frac{1}{4} = \frac{15}{8}$
Таким образом, результат деления $\frac{3}{4} \div \frac{2}{5}$ равен $\frac{15}{8}$.
Важно помнить, что при делении дробей необходимо инвертировать делитель и умножить его на делимое. После получения результата рекомендуется сократить дробь, если это возможно.
Приведение дробей к общему знаменателю
Для приведения дробей к общему знаменателю необходимо выполнить следующие шаги:
- Найти наименьшее общее кратное (НОК) знаменателей всех дробей. Для этого необходимо разложить каждый знаменатель на простые множители и выбрать наибольшую степень каждого простого множителя, присутствующего в разложении.
- Умножить каждую дробь на число, равное отношению НОК к знаменателю этой дроби.
- Полученные дроби будут иметь одинаковый знаменатель, что позволяет проводить операции с ними.
Приведение дробей к общему знаменателю позволяет упростить дальнейшую работу с дробями, так как дроби с одинаковым знаменателем можно складывать, вычитать и сравнивать намного проще. Также это помогает в решении различных задач, связанных с долями, долями величин и т. д.
Решение задач на дроби с помощью уравнений
Для решения задач на дроби в 6 классе по учебнику Мерзляк можно использовать метод уравнений. Этот метод основывается на том, что дроби можно представить в виде уравнения.
Для начала, необходимо формализовать условие задачи и выразить его в виде уравнения с неизвестными величинами. Затем, используя свойства дробей, решаем полученное уравнение и находим значения неизвестных.
Приведем пример решения задачи с помощью уравнений:
Задача: Дана дробь, числитель которой больше знаменателя на 3. Если увеличить числитель на 4 и знаменатель на 1, то получится дробь 2/3. Найдите исходную дробь.
Решение: Пусть исходная дробь — x. Исходя из условия задачи, составим уравнение:
| x | x+3 |
| — | — = 2/3 |
| 1 | 1 |
Решим полученное уравнение:
| x | x+3 |
| — | — = 2/3 |
| 1 | 1 |
Умножим оба числители и знаменатели на 3, чтобы избавиться от знаменателя:
| 3x | 3(x+3) |
| — | — |
| 3 | 3 |
Получаем:
| 3x | 3(x+3) |
| — | — |
| 3 | 3 |
Раскроем скобки:
| 3x | 3x + 9 |
| — | — |
| 3 | 3 |
Теперь получаем уравнение:
| 3x | 3x + 9 |
| — | — |
| 3 | 3 |
Решаем полученное уравнение:
| 3x + 9 = 2x |
Получаем:
| x = -9 |
Таким образом, исходная дробь равна -9/3 или -3.
Таким образом, метод уравнений позволяет решать задачи на дроби в 6 классе по учебнику Мерзляк, представляя дроби в виде уравнений и решая их с помощью свойств дробей.
Проценты и дроби

Проценты выражают долю числа от 100. Например, 50% означает половину от целого, а 25% – четверть. Проценты обозначаются символом % и могут быть записаны в виде десятичной дроби. Например, 50% = 0,5, а 25% = 0,25. Для перевода процентов в десятичную дробь используется следующая формула: десятичная дробь = процент / 100.
Дроби, в свою очередь, представляют собой отношение одного числа к другому. Они могут быть обыкновенными (с числителем и знаменателем) или десятичными. С помощью дробей можно выразить доли и доли от долей. Например, 1/2 – это половина, а 3/4 – три четверти.
В задачах по процентам и дробям 6 класса часто требуется найти процент от числа или найти число, соответствующее заданному проценту. Для решения таких задач можно использовать умножение и деление дробей. Например, чтобы найти 25% от числа, нужно умножить это число на 25/100 или на 0,25.
Кроме того, проценты и дроби используются при сравнении долей и нахождении их суммы или разности. Например, чтобы сравнить доли 2/3 и 3/4, их можно привести к общему знаменателю и сравнить числители.
Умение работать с процентами и дробями является важной математической компетенцией, которая активно используется в повседневной жизни. Знание этих тем позволяет правильно считать скидки, налоги, процентные ставки и многое другое.
Таким образом, изучение процентов и дробей в 6 классе по учебнику Мерзляк помогает развить навыки работы с числами, логическое мышление и практическую математическую грамотность.
Практические задачи по дробям
Рассмотрим несколько практических задач по дробям:
| Задача 1: | Витя выпил 3/4 литра молока, а Катя выпила 2/3 литра молока. Сколько молока выпили они вместе? |
| Задача 2: | У Маши было 5/6 кг яблок, а у Васи — 7/8 кг яблок. Сколько яблок было у них вместе? |
| Задача 3: | Аня пробежала 2/3 дистанции, а Маша — 5/6 дистанции. Какую долю всей дистанции пробежали девочки вместе? |
Для решения этих задач необходимо сложить или вычесть дроби с одинаковыми знаменателями. Если знаменатели различны, нужно привести дроби к общему знаменателю и затем произвести операции.
Решение задач по дробям требует внимательности и понимания основных правил работы с дробями. Постоянная практика поможет улучшить навыки и научиться решать задачи более эффективно.
Вопрос-ответ:
Как решать задачу, где нужно сложить две дроби?
Для сложения двух дробей нужно привести их к общему знаменателю, затем сложить числители и записать результат над общим знаменателем. Например, если нужно сложить 1/3 и 2/5, найдем общий знаменатель, который будет равен 15. Первую дробь умножим на 5/5, а вторую — на 3/3, чтобы получить дроби с общим знаменателем. После этого сложим числители: 1/3 * 5/5 + 2/5 * 3/3 = 5/15 + 6/15 = 11/15. Итак, сумма дробей 1/3 и 2/5 равна 11/15.
Как упростить дробь в задаче?
Дробь можно упростить, если числитель и знаменатель делятся на одно и то же число. Например, если у нас есть дробь 4/8, то ее можно упростить, разделив числитель и знаменатель на их наибольший общий делитель (НОД), который в данном случае равен 4. Делим числитель и знаменатель на 4: 4/8 ÷ 4/4 = 1/2. Итак, дробь 4/8 упрощается до 1/2.
Как решить задачу, где нужно вычесть одну дробь из другой?
Для вычитания одной дроби из другой нужно привести их к общему знаменателю, затем вычесть числители и записать результат над общим знаменателем. Например, если нужно вычесть 1/3 из 2/5, найдем общий знаменатель, который будет равен 15. Первую дробь умножим на 5/5, а вторую — на 3/3, чтобы получить дроби с общим знаменателем. После этого вычтем числители: 2/5 * 3/3 — 1/3 * 5/5 = 6/15 — 5/15 = 1/15. Итак, разность дробей 2/5 и 1/3 равна 1/15.
Как решить задачу, где нужно умножить две дроби?
Для умножения двух дробей нужно перемножить числители и знаменатели этих дробей. Например, если нужно умножить 2/3 на 4/5, перемножим числители и знаменатели: 2/3 * 4/5 = 8/15. Итак, произведение дробей 2/3 и 4/5 равно 8/15.
Какие принципы стоит учитывать при решении задач по дробям в 6 классе?
При решении задач по дробям в 6 классе стоит учитывать следующие принципы: 1) провести анализ условия задачи и выделить ключевые моменты; 2) определить тип задачи (сложение дробей, вычитание дробей, умножение дробей, деление дробей) и выбрать подходящую стратегию решения; 3) выполнить необходимые действия с дробями; 4) проверить полученный ответ и сделать выводы. Важно также обратить внимание на правильное использование алгоритмов и формул для работы с дробями.
Какие методы можно использовать при решении задач на сложение и вычитание дробей в 6 классе?
При решении задач на сложение и вычитание дробей в 6 классе можно использовать следующие методы: 1) поиск общего знаменателя и приведение дробей к общему знаменателю; 2) использование алгоритма «умножение на единицу» для приведения дробей к одинаковому знаменателю; 3) использование алгоритма «умножение на дополнение» для приведения дробей к одинаковому знаменателю; 4) использование алгоритма «складывание целых частей» при сложении смешанных чисел. Важно также уметь выполнять действия с числами, имеющими различные знаки.
Как решить задачу по умножению дробей в 6 классе?
Для решения задачи по умножению дробей в 6 классе нужно выполнить следующие шаги: 1) определить тип задачи и выделить ключевые моменты условия; 2) записать выражение для умножения дробей; 3) выполнить умножение числителей и знаменателей; 4) упростить полученную дробь, если это возможно; 5) проверить полученный ответ и сделать выводы. Необходимо также знать правила умножения дробей и уметь приводить полученные дроби к простейшему виду.
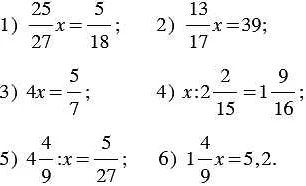


Статья очень полезна для учеников 6 класса, так как она подробно описывает, как решать задачи по дробям по учебнику Мерзляк. Материал представлен доступно и понятно, что особенно важно для учеников, которые только начинают изучать эту тему. Я, как реальный читатель, нашел много полезной информации. Особо понравилось, что статья дает примеры решения различных задач, что помогает лучше понять материал и усвоить его. Примеры подробно разбираются, поэтому нет проблем с пониманием каждого шага решения. Кроме того, статья также содержит полезные советы и подсказки, которые помогут ученикам справиться с трудностями при решении задач по дробям. Это важно, так как математика может быть сложной для некоторых учеников, и дополнительные советы и подсказки помогут им улучшить свои навыки. Я бы рекомендовал эту статью всем ученикам 6 класса, которые хотят лучше разобраться в решении задач по дробям. Статья понятна, информативна и содержит много полезных примеров и советов. Она поможет вам улучшить свои математические навыки и успешно решать задачи по дробям.