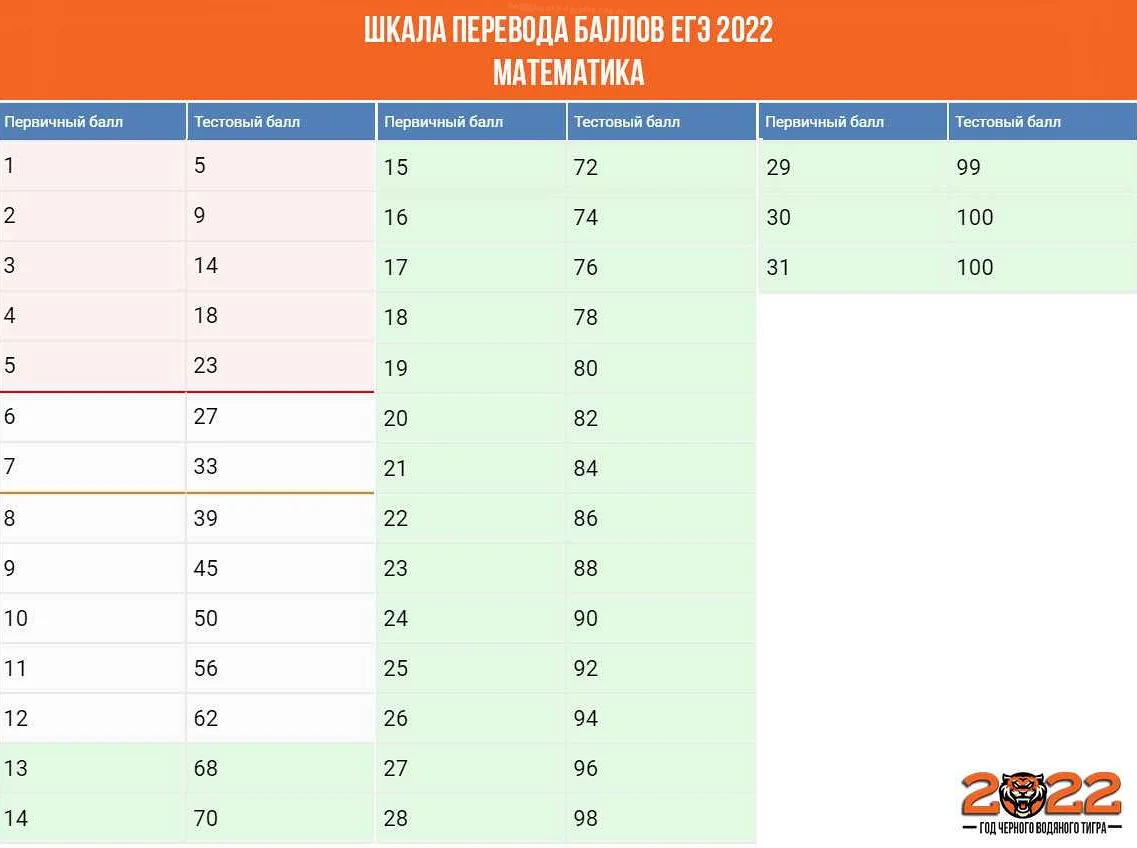
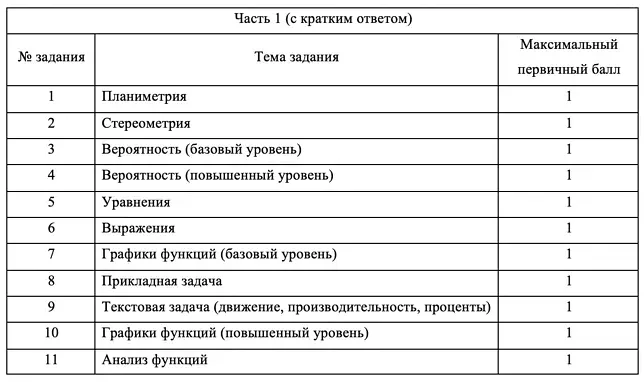
17 задание ЕГЭ по математике профильного уровня: правильное решение шаг за шагом

Получите подробные рекомендации, как решить 17 задание ЕГЭ по математике профильного уровня, с нашей статьей. Мы предоставляем полезные советы и примеры для понимания сложных задач, которые встречаются на экзамене. Наши рекомендации помогут улучшить результаты и повысить уверенность в будущем экзамене.

17 задание ЕГЭ по математике профильного уровня известно своей сложностью и требовательностью к знаниям. Оно проверяет способность абитуриента применять различные математические методы и анализировать информацию.

В этой статье мы предоставим подробный разбор 17 задания ЕГЭ по математике профильного уровня, а также дадим полезные советы по ее решению. Мы разберем различные варианты задач, выявим и объясним главные трудности и дадим проверенные методы решения задания.

Если вы готовитесь к ЕГЭ по математике профильного уровня, то наша статья будет полезной для вас. Она поможет разобраться в теме и готовиться к экзамену наиболее эффективным образом. Не откладывайте подготовку на последний момент, начните готовиться к своему успеху сейчас!

Как сдать 17 задание ЕГЭ по математике профильного уровня: подробный разбор и полезные советы

17 задание ЕГЭ по математике профильного уровня является одной из самых сложных задач экзамена. Оно требует не только знания математических формул, но и умения применять их в реальной жизни. Именно поэтому подготовка к этому заданию должна быть тщательной и основательной.

Во-первых, необходимо внимательно изучить условие задачи и сформулировать ее математическую модель. Затем следует составить соответствующее уравнение, учитывая все известные данные и неизвестную величину.

Во-вторых, необходимо научиться работать с графиками и функциями. Задача может потребовать построения графика или уравнения функции, а также вычисления интегралов и производных.

В-третьих, необходимо научиться анализировать полученные результаты и делать правильные выводы. При решении задачи необходимо проверить правильность ответа, а также оценить его адекватность и соответствие условию задачи.

Хорошей практикой является решение большого количества задач, схожих с 17 заданием ЕГЭ. Это поможет закрепить знания и научиться применять их на практике.

Будьте внимательны и не торопитесь. Экзамен временно ограничен, но для решения 17 задачи не стоит тратить слишком много времени и усилий. Следуйте логике решения и действуйте шаг за шагом.

Воспользуйтесь этими советами и подготовьтесь к 17 заданию ЕГЭ по математике профильного уровня тщательно и основательно, чтобы пройти экзамен успешно и получить высокие баллы.

Понимание условия задания

Одной из ключевых составляющих успешного решения 17 задания ЕГЭ по математике профильного уровня является понимание условия задания. Важно уделить достаточно времени на изучение всех выражений, формул и условий, прежде чем начать работу над решением задания.

В условии задания обычно содержится вся необходимая информация для его успешного решения. Важно внимательно изучить все выражения, обратить внимание на обозначения переменных и констант. Иногда в задании могут содержаться дополнительные сведения, например, о пределах изменения переменных, что может помочь при работе с формулами.

Также стоит обратить внимание на формулировки условий. В тексте задания может быть использован язык предикатов, который может звучать несколько запутано и многословно. Важно разобраться в том, какие факты сказаны прямо, а какие имеются в виду косвенно.

Важно понимать, что 17 задание ЕГЭ по математике профильного уровня может иметь несколько вариантов формулировки условия. Поэтому, при подготовке к экзамену необходимо изучать различные варианты заданий и закреплять свои знания на примерах.

Имейте в виду, что понимание условия задания является ключом к успешному решению задачи и, следовательно, к получению высокого балла за экзамен.

Определение балльной стоимости задания

Каждое задание в ЕГЭ имеет определенную балльную стоимость, назначаемую экспертами, проверяющими работы участников. Баллы за задание зависят от общего количества баллов в задании, а также от сложности и уровня требований к решению.

Уровень сложности задания определяется тематикой, требованиями к решению и количеством этапов решения. Большинство заданий основаны на знаниях и умениях, полученных в ходе изучения предмета в школе и не требуют дополнительных знаний.

Проверяющие работу участника собирают баллы за задание, учитывая правильность решения, постановку задачи и ее оформление. Если участник составил правильный алгоритм и решение, он получает максимальное количество баллов. Однако, если у него есть недочеты в решении или оформлении задания, он может потерять часть баллов.

Оценка задания назначается на основании общего количества баллов, которое может получить участник. Общее количество баллов зависит от темы задания и сложности решения. Обычно, это от 1 до 4 баллов за задание.

Таким образом, чтобы получить максимальную оценку, участник должен не только правильно решить задание, но и правильно оформить его и выполнить все требования, указанные в задании. Только в этом случае он сможет получить максимальное количество баллов и высокую оценку.

Анализ примеров решения задания

При анализе примеров решений задания 17 ЕГЭ по математике профильного уровня можно выделить несколько подходов к решению:

• Приложение теоремы о сравнении бесконечно малых.
• Применение логарифмических преобразований.
• Использование метода математической индукции.

Приложение теоремы о сравнении бесконечно малых заключается в сравнении значения функции приближенно с ее пределом при бесконечном значении переменной. Данный метод требует хорошего знания математического аппарата и умения применять его на практике.

Применение логарифмических преобразований позволяет упростить выражения и свести задачу к поиску корня уравнения. Такой подход удобен в случаях, когда сложность задачи состоит в вычислении многочленов и тригонометрических функций.

Использование метода математической индукции позволяет доказать верность утверждения для всех натуральных значений переменной. Такой метод подходит для решения задач, которые можно свести к формуле с n+1 членом по сравнению с n членами.

Особенности решения задания на графике

Решение задания на графике требует некоторых специфических знаний и навыков. Важно понимать, что график — это визуализация математической функции, которая может помочь в нахождении различных значений и связей между переменными.

Для начала, нужно уметь определить тип функции по ее графику. Например, если график является прямой линией, то это указывает на линейную функцию. Если график имеет кривую форму, то это может указывать на квадратичную, синусоидальную или логарифмическую функцию.

Важно также учитывать особенности графика, такие как точки пересечения с осями координат, максимальные и минимальные значения функции, места экстремумов и т.д. Эти характеристики могут помочь в решении задач на определение значений функции или нахождение экстремумов.

Кроме того, стоит уметь использовать координатную плоскость для построения графиков функций и анализа их свойств. Это может потребоваться в задачах на определение асимптот, границ области определения или нахождение точек перегиба.

Наконец, необходимо сделать выводы на основе анализа графика и возвращаться к условию задачи, чтобы проверить правильность полученного решения. В целом, умение работать с графиками функций — это важный навык для решения задач на математической ЕГЭ.

Полезные математические формулы и определения

Формула суммы арифметической прогрессии:

Сумма n первых членов арифметической прогрессии с первым членом a и разностью d:

Sn = (n/2) * (2a + (n-1)d)

Формула суммы геометрической прогрессии:

Сумма n членов геометрической прогрессии с первым членом a и знаменателем q:

Sn = a((1-qn)/(1-q))

Теорема Пифагора:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:

a2 + b2 = c2

Формула Эйлера:

Для любого натурального числа n выполнено:

eix = cos(x) + i * sin(x)

Формула Герона:

Площадь треугольника со сторонами a, b, c вычисляется по формуле:

S = √p(p-a)(p-b)(p-c), где p = (a+b+c)/2 — полупериметр

Определения:

1. Функция — отображение множества в другое множество
2. Производная — мера изменения функции при изменении аргумента
3. Интеграл — площадь фигуры, ограниченной графиком функции и осями координат
4. Матрица — таблица чисел, упорядоченных по строкам и столбцам

Секреты эффективного временного планирования

1. Определение приоритетов

Первый шаг к эффективному временному планированию — это определение приоритетов. Составьте список всех задач, которые нужно выполнить, и распределите их по степени важности. Затем составьте список задач, которые нужно выполнить в ближайшее время.

2. Оптимальное использование времени

Очень важно использовать свое время оптимально. Разработайте график работы, учитывая продуктивные часы и перерывы. Не забывайте про время на отдых.

3. Блокирование времени

Блокирование времени — это метод разбиения времени на блоки и фокусирование на выполнении определенных задач в течение каждого блока времени. Это поможет повысить продуктивность и сосредоточиться на значимых задачах.

4. Использование технологических инструментов

Существуют многочисленные технологические инструменты для улучшения эффективности временного планирования. Они включают в себя приложения для управления задачами, календари и таймеры.

5. Гибкий график работы

Гибкий график работы может помочь справиться с неожиданностями и задержками в работе. Разработайте график работы, учитывая не только основные задачи, но и возможные задержки.

6. Оценка результатов

Нельзя забывать оценку результатов временного планирования. Анализируйте потраченное время и количество выполненных задач. Это поможет улучшить свои навыки планирования в будущем.

Вывод

Эффективное временное планирование требует определения приоритетов, оптимального использования времени, блокирования времени, использования технологических инструментов, гибкого графика работы и оценки результатов. Применение этих секретов поможет достигать поставленных целей и повышать эффективность своей работы.

Техники проверки ответов на правильность

Одна из наиболее распространенных ошибок при решении задач ЕГЭ – неправильная проверка ответов. Ниже приведены несколько полезных техник, которые помогут избежать эту ошибку:

• Переход к исходному условию: вспомните, какие данные даны в исходном условии задачи и сверьте их с тем, что вы использовали для решения. Если какой-то параметр отличается или не учитывается, то вероятно, что ответ неправильный.
• Подстановка ответа: если у вас есть уравнение или система уравнений, подставьте свой ответ и проверьте, выполняется ли равенство. Если да – ответ верный.
• Графический метод: если возможно, нарисуйте график функции или системы уравнений и проверьте, совпадает ли он с тем, что вы получили в результате решения.
• Простая логика: оцените свой ответ логически. Например, если в задаче просили найти расстояние между двумя точками на плоскости, оно не может быть отрицательным. Если ваш ответ таков – он неправильный.
• Проверка через другую формулу: если для решения задачи есть несколько формул, используйте их для проверки ответа. Например, если задача была про определитель, посчитайте его еще раз используя другой способ.

Эти техники помогут вам проверить ваш ответ на правильность и существенно уменьшить количество ошибок в решении задач. Не забывайте, что проверка ответов – это часть решения задачи и стоит отдельного времени и внимания!

Как не допустить ошибок при решении задания

1. Тщательно прочитайте условие задачи.

Перед тем, как начать решать задание, более чем рекомендуется тщательно прочитать условие. Не забудьте, что в условии задачи может быть указано, какие формулы и свойства можно использовать.

2. Проанализируйте данные.

Перед тем, как приступить к решению задачи, проанализируйте предоставленные данные и убедитесь, что все известные величины учтены и правильно записаны. Другими словами, проверьте данные, чтобы не допустить ошибок в решении.

3. Выберите подходящую стратегию решения задачи.

Каждая задача уникальна и требует своего собственного подхода. Необходимо выбрать наиболее подходящую стратегию решения задачи.

4. Проверьте арифметические операции.

Одной из причин ошибок является неправильное использование арифметических операций, таких как умножение, деление, сложение и вычитание. Первым шагом, чтобы избежать таких ошибок, проверьте арифметические операции, выполненные в решении.

5. Проверьте свою работу.

Перед тем, как сдать работу, внимательно проверьте свое решение. Попросите кого-нибудь другого, чтобы он или она тоже прочитал решение, и проверьте свою работу на ошибки.

Наконец, не забудьте: отнеситесь к решению задания спокойно и не паникуйте. Если вы не понимаете, как решить задание, попробуйте сделать шаг назад и подумать логически. Если же вы все-таки не можете решить задачу, не стоит спешить – вы можете пропустить ее и вернуться к ней позже.

Часто допускаемые ошибки и их устранение

1. Неправильная запись уравнений и неравенств. Важно внимательно читать условия задач и правильно записывать уравнения и неравенства. Чаще всего ошибки возникают из-за неправильного перевода условия в математические символы. Старайтесь использовать привычные обозначения и не забывайте про знаки равенства и строгости.

2. Ошибки при работе с процентами. Работа с процентами требует внимательности и точности. Многие ошибки возникают при расчете процентных долей, прибавлении или вычитании процентов от числа. Не забывайте также про различия между процентами и долями.

3. Ошибки при работе с графиками и координатами. При работе с графиками и координатами часто допускаются ошибки при определении точек пересечения, построении прямых и графиков функций. Важно не только уметь правильно решать задачи, но и грамотно и красиво оформлять графики и рисунки.

4. Неправильное использование формул и алгоритмов. В математике очень важно знать и правильно использовать формулы и алгоритмы, особенно в задачах, связанных с геометрией и тригонометрией. Часто ошибки возникают из-за неправильного применения формул или алгоритмов, неумения использовать подходящие методы.

5. Ошибки при работе с векторами и матрицами. Ошибки при работе с векторами и матрицами связаны как с неправильным пониманием этих объектов, так и с неумением правильно выполнять действия с ними. Важно не только знать определения и свойства векторов и матриц, но и уметь правильно их использовать в задачах.

6. Недостаток времени и неумение организовать свою работу. Наконец, одним из главных факторов, влияющих на успех в решении задач по математике, является неумение грамотно распределить свое время и правильно организовать свою работу. Важно не только знать материал и уметь решать задачи, но и быстро ориентироваться в условиях, выделять главное и использовать различные стратегии решения задач.

Рекомендации для подготовки к решению задания

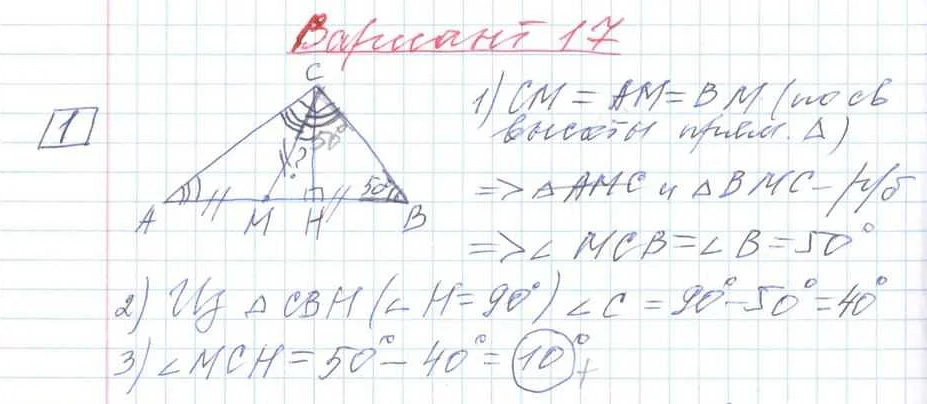
1. Изучите теорию: перед решением задания необходимо убедиться, что вы хорошо знакомы с теорией рассматриваемых тем. Для этого можно использовать учебник и различные интернет-ресурсы.

2. Решайте задачи: регулярное решение математических задач поможет укрепить понимание теории и развить навыки решения заданий. Рекомендуется решать задачи разной сложности, начиная с простых и заканчивая более сложными.

3. Анализируйте ошибки: в процессе решения задач необходимо следить за тем, какие ошибки вы допускаете, и анализировать причины их возникновения. Это поможет избежать повторения ошибок в будущем.

4. Практикуйте тайм-менеджмент: задание ЕГЭ имеет ограниченное время для решения, поэтому важно научиться управлять своим временем. Постепенно увеличивайте время, затрачиваемое на решение заданий, до тех пор, пока вы не сможете решить задание в отведенное время.

5. Используйте графические средства: в задании могут встречаться сложные графики и схемы, которые лучше быстро освоить и уметь к ним быстро обращаться. Рекомендуется использовать дополнительные макеты, на которых можно решать различные графические задачи.

6. Следите за новостями: ЕГЭ по математике на профильном уровне требует знаний не только стандартной математической теории, но и ее приложений в реальной жизни. Поэтому полезно следить за новостными сообщениями, связанными с математическими открытиями и приложениями в различных областях науки.

Экспертный совет по сдаче ЕГЭ по математике профильного уровня

Подготовка к ЕГЭ по математике профильного уровня необходима начинать заранее. Не важно, какие знания вы имеете сейчас, важно учиться систематически и регулярно повторять изученный материал.

Не ограничивайте себя только учебником. Изучайте решения задач, просматривайте видеоуроки, читайте специальную литературу и смотрите советы экспертов.

Не забывайте практиковаться в решении задач. После изучения каждой темы решайте несколько упражнений, проверяя свои знания.

В день экзамена не забывайте про правильное распределение времени. Для решения заданий разных уровней необходимо иметь представление об оставшемся времени на экзамене.

Наконец, не забывайте про внимательность. Прежде чем приступать к решению задачи, читайте условие задачи несколько раз и обращайте внимание на все детали.

Вопрос-ответ:

Что такое 17 задание ЕГЭ по математике профильного уровня?

17 задание ЕГЭ — это одно из заданий, которое предлагается выполнять на экзамене по математике профильного уровня. Оно относится к разделу «Производные и исследование функций».

Какие навыки необходимы для решения 17 задания ЕГЭ по математике профильного уровня?

Для успешного решения 17 задания ЕГЭ необходимо знание основных понятий и теорем, связанных с производными и исследованием функций. Также необходимо уметь применять эти знания на практике и быстро выполнять расчеты.

Какие ошибки чаще всего допускаются при решении 17 задания ЕГЭ по математике профильного уровня?

Наиболее распространенной ошибкой при решении 17 задания ЕГЭ является неверное применение теорем и формул. Также часто допускаются ошибки при расчетах и неправильное определение экстремумов и точек перегиба функции.

Какие приемы помогут ускорить решение 17 задания ЕГЭ по математике профильного уровня?

Один из приемов, который поможет ускорить решение задания — это использование готовых таблиц производных и нахождение экстремумов и точек перегиба методом знаков. Также необходимо учитывать время и разбирать задание по пунктам, решая каждый пункт по отдельности.

Какие материалы помогут подготовиться к решению 17 задания ЕГЭ по математике профильного уровня?

Для подготовки к решению 17 задания ЕГЭ по математике профильного уровня можно использовать специальные учебники и пособия, которые содержат теорию, примеры и задания. Также полезно решать практические задания из прошлых годовых экзаменов и тренировочные задания.

Какие факторы могут повлиять на результат решения 17 задания ЕГЭ по математике профильного уровня?

Результат решения 17 задания ЕГЭ может зависеть от многих факторов, таких как уровень подготовки, скорость выполнения расчетов, умение ориентироваться в условии задачи и правильно применять теоремы и формулы. Также важным фактором является концентрация внимания и эмоциональное состояние.

Можно ли сдать ЕГЭ по математике профильного уровня без решения 17 задания?

Решение 17 задания ЕГЭ при сдаче математики профильного уровня является обязательным. Без выполнения этого задания экзамен считается несданным. Поэтому необходимо уделить достаточно времени подготовке и тренировке перед экзаменом.

Видео по теме: