Как выполнить задание по математике в 6 классе: номер 268 с объяснениями и примерами

Узнайте, как решить задачу по математике 6 класса номер 268 с помощью простых шагов и подробных объяснений. Сделайте свою учебу более эффективной и легкой с нашими советами и рекомендациями.

Математика – это предмет, который многие ученики считают сложным и непонятным. Однако, если подходить к нему с правильной стороны, то он может стать одним из самых любимых предметов. В этой статье мы рассмотрим задание по математике 6 класс № 268 и покажем, как его решить.

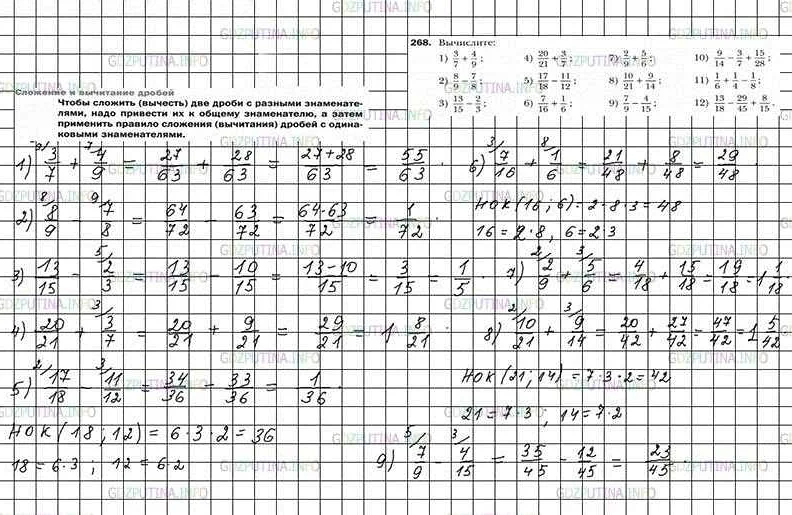
Задание № 268 состоит из нескольких пунктов, каждый из которых требует определенных знаний и умений. Мы пошагово разберем каждый пункт и дадим подробные объяснения и примеры, чтобы вы легко освоили материал.

Мы также предоставим вам решения для каждого пункта задания, чтобы вы могли проверить свои ответы и убедиться в правильности выполнения. Итак, приступим к решению задания по математике 6 класс № 268!

Как решить математику 6 класс № 268: подробная инструкция с примерами и решениями

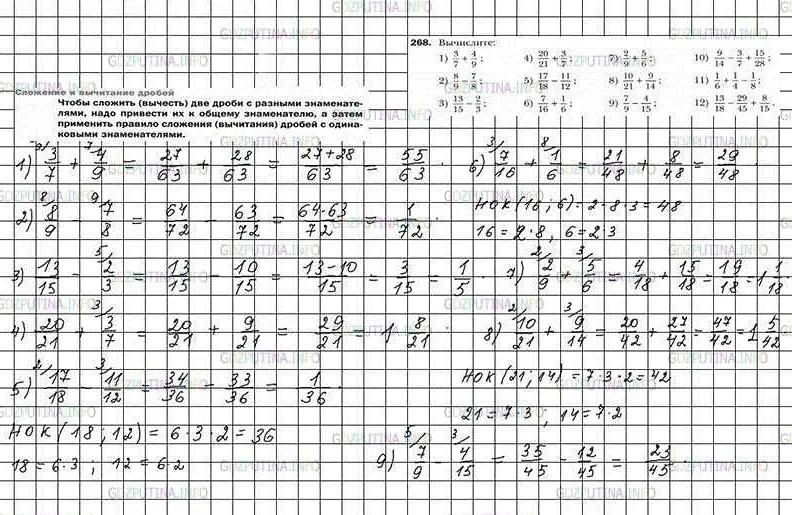
Школьная математика может показаться сложной задачей, особенно если вы только начали обучение. Тем не менее, с помощью правильного подхода и тщательного изучения данных задач, вы можете сделать эту науку проще и более доступной для понимания. Ниже приведена подробная инструкция по решению задания по математике 6 класс № 268, включающая примеры и решения.

Шаг 1: Полное понимание задачи

Перед тем, как начать решать задачу, необходимо полностью понимать условия и требования задачи. Тщательно прочитайте задание и определите, что требуется от вас. Затем сконцентрируйтесь на ключевых словах, которые помогут вам определить, какой тип решения требуется: арифметический, геометрический или логический.

Шаг 2: Правильное применение формул и алгоритмов

После того, как вы понимаете задание и знаете, какой тип решения требуется, необходимо правильно применять формулы и алгоритмы. Некоторые задачи могут потребовать проценты, десятичные дроби или пропорции. В таких случаях необходимо знать все соответствующие формулы и уметь их применять.

Шаг 3: Изображение графиков и диаграмм

В некоторых задачах может потребоваться построение графиков или диаграмм. Убедитесь, что вы знаете правильный подход к построению этих графиков и диаграмм и что представленные на них данные точны и понятны.

Шаг 4: Проверка решения

После того, как вы закончили решать задачу, обязательно проверьте свое решение. Убедитесь, что все формулы и алгоритмы были правильно применены, и что ответ является логичным и точным. Если вы уверены в правильности своего ответа, перепроверьте его с помощью другой методики или проверьте его еще раз вместе с учителем или старшим.

Пример решения задачи

Допустим, наша задача звучит следующим образом: «Выходя из дома в школу, Марина прошла 500 метров, а затем повернула направо и прошла еще 300 метров. На каком расстоянии от дома она оказалась?»

Чтобы решить эту задачу, мы можем использовать формулу Пифагора. Согласно ей, длина гипотенузы квадрата равна сумме квадратов длин двух катетов. В нашем случае, 500 метров и 300 метров являются катетами.

Шаг 1: в нашей задаче Марина проходит расстояние 500 метров и затем 300 метров.

Шаг 2: используйте формулу Пифагора для определения длины гипотенузы квадрата.

• 500² + 300² = X²
• 250000 + 90000 = X²
• 340000 = X²
• X = √340000 ≈ 583.1

Ответ: Марина оказалась на расстоянии около 583 метров от дома.

Видео по теме:

О чем статья

В данной статье рассматривается пример задания по математике для учеников 6 класса, а именно, задание № 268. Мы подробно разберем каждый пункт задания, и предоставим подробные инструкции по его решению. Кроме того, в статье приведены примеры решения задания и пошаговые инструкции для их получения.

Математика для многих учеников является довольно сложным предметом, однако с правильным подходом и регулярной практикой решения заданий, каждый ученик может справиться с поставленной задачей. В статье мы опишем не только решение данного задания, но и предоставим полезные советы и рекомендации, которые помогут ученикам лучше понять математические концепции и методики решения заданий.

При выполнении задания № 268 мы будем использовать различные методы решения, в том числе методы геометрической работы, алгебры, арифметики и др. В этой статье мы сделаем все возможное, чтобы материал был изложен максимально понятно и доступно для каждого ученика. Решение заданий по математике не только развивает логическое мышление, но и помогает улучшить навыки работы с цифрами и теорию чисел, что непременно пригодится каждому в будущем.

Подготовка к решению

Перед тем как приступить к решению задачи № 268 по математике 6 класса, необходимо ознакомиться с условием задачи и понять, что от вас требуется. Важно прочитать задание несколько раз, чтобы не упустить важные детали, которые могут оказаться ключевыми для решения.

Также необходимо убедиться, что вы понимаете все математические понятия и формулы, которые используются в задаче. Если у вас возникнут затруднения с пониманием каких-либо терминов или с формулами, необходимо обратиться к учебнику и изучить соответствующую тему.

Для успешного решения задачи может помочь составление плана и последовательности действий. При составлении плана стоит обратить внимание на ключевые элементы и шаги, которые необходимо выполнить. Планирование поможет структурировать задание и избежать ошибок.

• Ознакомиться с условием задачи и понять, что от вас требуется;
• Убедиться, что вы понимаете все математические понятия и формулы;
• Составить план и последовательность действий;
• Выполнить задание, следуя плану;
• Проверить полученный результат и убедиться, что он соответствует условию задачи.

При решении задачи № 268 по математике 6 класса также стоит обратить внимание на правильность выполнения арифметических операций и на точность расчетов. Не забывайте о том, что каждый шаг должен быть подробно обоснован и доказан, чтобы результат был верным.

Вопрос-ответ:

Как решить задание № 268, если не знаю формулу исключения неправильных корней?

Для решения задания № 268 необязательно знать формулу исключения неправильных корней. Можно воспользоваться алгоритмом решения квадратных уравнений через выделение полного квадрата. Пример решения дан в статье.

Почему в результате решения задания у нас получается два корня?

При решении квадратного уравнения могут быть только два корня – это связано с теорией квадратных уравнений. Эти корни могут быть разными или совпадающими, но их количество всегда будет два.

Как понять, что уравнение является квадратным?

Уравнение называется квадратным, если переменная в нем входит в степень два и не входит в более высокие степени. Например, уравнение x^2 + 3x — 4 = 0 является квадратным.

Как правильно работать со знаками при решении квадратного уравнения?

При решении квадратного уравнения необходимо следить за знаками. Если перед x^2 стоит знак минус, то при переносе этого слагаемого на другую сторону знак меняется на плюс. Также нужно помнить, что если знак перед x не определен, то его можно выбрать самостоятельно. Например, можно положить x = a и решить уравнение a^2 = 4, а затем полученное решение подставить в исходное уравнение и определить знак перед x.

Какие ошибки часто допускают при решении квадратных уравнений?

Одной из наиболее распространенных ошибок при решении квадратных уравнений является неправильный знак перед x при переносе слагаемых из одной части уравнения в другую. Также можно ошибиться при вычислении дискриминанта, совершив ошибки при перемножении, сложении и вычитании дробей. Для того, чтобы избежать ошибок, важно внимательно следить за каждым шагом решения и не спешить.

Как найти дискриминант квадратного уравнения?

Дискриминант квадратного уравнения ax^2 + bx + c = 0 вычисляется по формуле D = b^2 — 4ac. Он показывает, сколько корней имеет это уравнение: если D > 0, то уравнение имеет два корня, если D = 0, то корень единственный, а если D < 0, то уравнение не имеет действительных корней.

Можно ли решить квадратное уравнение без помощи дискриминанта?

Да, квадратное уравнение можно решить без вычисления дискриминанта, используя другие методы. Например, можно выразить один из корней через другой и тогда найти его значение. Или можно выделить полный квадрат и затем решить полученное уравнение. Однако вычисление дискриминанта является наиболее универсальным и надежным методом решения квадратного уравнения.

Анализ условия задачи

Перед тем как приступить к решению задачи, необходимо внимательно проанализировать условие. Прочтите его несколько раз, выделите ключевые слова и фразы, определите, что требуется найти, какие данные имеются и что известно о неизвестном значении. Если что-то не понятно, перечитайте и постарайтесь более детально разобраться.

Важно учесть все ограничения, которые указаны в условии задачи. Например, возможно, что ответ должен быть неотрицательным числом или что ответ должен быть выражен в определенных единицах измерения.

Также оцените уровень сложности задачи и подумайте о возможных способах ее решения. Некоторые задачи можно решить просто перебором значений, а для других может потребоваться использовать формулы и математические операции. Не забывайте также о проверке результата и ответа на разумность.

• Прочтите условие задачи несколько раз;
• Выделите ключевые фразы;
• Определите именно что требуется найти;
• Оцените уровень сложности задачи;
• Выберите способ решения;
• Не забудьте проверить результаты.

Соблюдение данных рекомендаций позволит упростить решение задачи и сделать его более быстрым и эффективым.

Определение неизвестных величин

Каждое математическое уравнение содержит неизвестные величины, которые нужно найти для того, чтобы решить уравнение. Перед решением задачи необходимо четко определить неизвестные величины и обозначить их, например, буквами x, y, z или любыми другими символами.

Обычно, в задачах по математике, используются разные виды неизвестных величин, такие как коэффициенты, переменные и константы. Коэффициенты выражают отношение между двумя величинами, переменные переменчивы и могут принимать различные значения, а константы – это постоянные значения, которые не изменятся в ходе решения задачи.

Важно запомнить, что неправильное определение неизвестных величин приведет к неверному результату. Поэтому перед началом решения задачи, нужно постараться понять, какие именно величины являются неизвестными и обозначить их.

Для лучшего понимания, можно использовать таблицу для записи неизвестных величин, указывая их символ, значения и единицы измерения. Это поможет не запутаться, особенно если в задаче используется несколько неизвестных величин.

Построение уравнения

Построение уравнения является важной частью решения задач в математике. Чтобы построить уравнение, необходимо провести анализ задачи и определить неизвестные величины.

Шаги построения уравнения:

• Определить неизвестные величины в задаче;
• Составить уравнение, используя известные данные и неизвестные величины;
• Решить уравнение, чтобы получить значение неизвестной величины.

Пример:

В задаче дано, что длина одной стороны квадрата равна 5 см больше длины другой стороны. Найдите длину каждой стороны квадрата.

• Неизвестные величины: длина стороны квадрата;
• Известные данные: длина одной стороны квадрата равна 5 см больше длины другой стороны (можно обозначить x и x+5);
• Уравнение: x + (x+5) = длина стороны квадрата (можно обозначить y);
• Решаем уравнение: 2x + 5 = y.

Таким образом, длина каждой стороны квадрата равна (2x+5)/2.

Решение уравнения

Решение уравнения – это процесс нахождения значения неизвестной переменной, которая удовлетворяет уравнению. Для решения уравнения необходимо применить последовательность математических операций, чтобы выразить неизвестную переменную.

Первый шаг в решении уравнения – это приведение его к форме, когда все члены с переменной на одной стороне уравнения, а все числовые значения – на другой стороне. Затем применяются арифметические операции, чтобы избавиться от переменной на одной стороне уравнения.

При решении уравнения необходимо учитывать правила алгебры, такие как закон сохранения равенства и умножение или деление обеих сторон уравнения на одно и то же число.

После выполнения всех арифметических операций и получения значения неизвестной переменной, необходимо проверить полученное решение, подставив его в уравнение и убедившись, что обе его стороны равны между собой.

Проверка правильности решения

Чтобы проверить правильность своего решения задачи, необходимо выполнить несколько шагов:

• Проверить правильность всех арифметических операций, которые были выполнены
• Убедиться, что все данные были правильно введены и использованы при решении
• Проверить, что ответ является корректным в контексте задачи

Если все шаги выполнены верно, можно быть уверенным в правильности решения задачи. Однако, если появляются сомнения, необходимо перепроверить каждый шаг, чтобы найти возможную ошибку. Не стоит забывать о дополнительных условиях, которые могут быть указаны в задаче, такие как ограничения по диапазону ответа, возможность оставления ответа в виде дроби и т.д.

Пример 1Шаги проверкиВывод

Задача: Найти площадь прямоугольника со сторонами 5 см и 7 см

Правильность арифметических операций: 5*7=35 Правильность введенных данных: стороны прямоугольника были указаны правильно Корректность ответа: площадь равна 35 кв. см

Решение правильное

Решение задачи на проценты

Задачи на проценты – одни из наиболее частых задач, которые можно встретить в школьной программе. Для решения задач на проценты необходимо знать формулу расчета процентов:

процент = (часть / целое) × 100%

Применение этой формулы позволяет решить задачу на проценты в несколько простых шагов. Например, рассмотрим задачу:

• Из 60 учеников школы на экскурсию поехали 90% учеников. Сколько учеников поехали на экскурсию?

Чтобы решить эту задачу, необходимо:

1. Найти количество учеников, которые поехали на экскурсию.
2. Использовать формулу расчета процентов.
3. Подставить известные значения в формулу и вычислить количество учеников.

Решение задачи:

Шаг 1	—	Найти количество учеников, которые поехали на экскурсию.	—	количество учеников, поехавших на экскурсию
Шаг 2	—	Использовать формулу расчета процентов: процент = (часть / целое) × 100%	—	процент поехавших на экскурсию = (количество учеников, поехавших на экскурсию / общее количество учеников) × 100%
Шаг 3	—	Подставить известные значения в формулу и вычислить количество учеников, которые поехали на экскурсию.	—	количество учеников, поехавших на экскурсию = (60 × 90%) = 54

Ответ: на экскурсию поехало 54 ученика.

Решение задачи на пропорции

Пропорция — это сравнение двух отношений. В математике она помогает решать задачи на доли или проценты. Рассмотрим пример:

Пример 1: К изготовлению 24 сникерса требуется 3 пачки муки. Сколько пачек муки требуется для изготовления 36 сникерсов?

1. Составляем пропорцию: 24 сникерса = 3 пачки муки
2. Находим соотношение муки на один сникерс: 3 пачки муки / 24 сникерса = 1/8 пачки муки на один сникерс
3. Находим количество муки для 36 сникерсов: 1/8 пачки муки на один сникерс x 36 сникерсов = 4.5 пачки муки

Ответ: для изготовления 36 сникерсов требуется 4.5 пачки муки.

Решение задачи на систему уравнений

Решение задач на систему уравнений – это процесс нахождения значений нескольких неизвестных переменных, удовлетворяющих одновременно нескольким уравнениям. Часто задачи на системы уравнений встречаются в математике, физике, экономике и других науках. Для решения задач необходимо использовать различные методы решения систем уравнений.

Одним из методов решения систем уравнений является метод подстановки. При этом методе необходимо выразить одну переменную через другую в одном уравнении и подставить это выражение в другое уравнение системы. Таким образом, уравнения сводятся к решению уравнения с одной переменной.

Другим методом решения систем уравнений является метод сложения. При этом методе необходимо сложить два уравнения системы таким образом, чтобы одна из переменных ушла, и решить получившееся уравнение с одной переменной. Затем, найдя значение этой переменной, можно подставить его в одно из исходных уравнений и найти значение другой переменной.

Также для решения задач на системы уравнений можно использовать матрицы и определители. При этом методе уравнения системы переписываются в матричной форме, а далее применяются соответствующие матричные операции для нахождения значений переменных.

Выбор метода решения задачи на систему уравнений зависит от порядка уравнений, количества неизвестных, а также личных предпочтений и опыта решения подобных задач. Важно не забывать проверять верность полученных значений, подставляя их в исходные уравнения системы.

Изучение ошибок при решении задачи

Решая задачи, мы часто допускаем ошибки. И когда задача решена неправильно, мы должны понять, в чем именно заключается ошибка. Изучение своих ошибок поможет лучше понять материал и не допустить ошибок в будущем.

Существует несколько способов изучения ошибок при решении задач. Один из них — переписывать решение задачи, анализируя каждый шаг. В процессе анализа можно обнаружить неправильный шаг и поправить его.

Другой способ — использование таблицы ошибок. В этой таблице мы записываем ошибку, которую допустили, и анализируем ее, что позволяет лучше понимать, какие типы ошибок мы совершаем чаще всего.

Важно также учитывать конструктивную критику, приходящую со стороны учителя или родителей. Они могут обнаружить ошибку, которую мы не заметили. Исправлять ошибки — это нормально, и важно не опускать руки, а продолжать учиться.

• Переписывайте решения задач, обнаруживая ошибки;
• Используйте таблицу ошибок;
• Учитывайте конструктивную критику.

Полезные советы и рекомендации

Подготовка к математике 6 класса требует усидчивости и системности. Нельзя надеяться на случай и сразу же решать сложные задания. Необходимо усвоить все теоретические материалы, чтобы уверенно решать практические задания.

Решая задачи, необходимо внимательно читать условия и проверять свои выкладки. Опечатки и невнимательность могут привести к неправильному результату. Если возникли затруднения, не паникуйте, лучше остановитесь и перечитайте условия, либо обратитесь к подсказкам и готовым решениям.

Старайтесь пользоваться формулами, таблицами и схемами, чтобы оптимизировать свою работу. Формулы помогут вам сократить время и избежать ошибок. Также не забывайте о значении единиц измерения в задачах, например, метры или километры, граммы или килограммы.

• Повторение материала и тренировки – ключ к успеху в математике.
• Не перенапрягайте глаза и не просиживайте долго за учебниками, проводите перерывы и занимайтесь спортом.
• Ставьте перед собой цели и находите мотивацию.
• Найти дополнительный материал в Интернете, что может помочь вам получить дополнительную практику.

Надеемся наши рекомендации помогут вам успешно справиться с математикой 6 класса. Успехов вам!