Эффективные способы решения 1.5 задания ОГЭ по математике 2021 года на примере задачи про теплицу

Решение задания 1.5 по математике для ОГЭ 2021 на примере задачи про теплицу. Подробные пошаговые инструкции для успешной сдачи экзамена.

В задании 1.5 по математике на ОГЭ 2021 года требуется решить задачи на тему «Теплица». Некоторые школьники могут столкнуться с трудностями, поэтому в этой статье мы представим несколько примеров решения задач на эту тему.

Теплица – это здание, предназначенное для выращивания растений. В задачах на тему «Теплица» обычно требуется найти площадь или объем теплицы, или рассчитать количество растений, которые можно выращивать в теплице.

Для решения задач на тему «Теплица» важно знать формулы для нахождения площади и объема прямоугольного параллелепипеда (это базовые формулы для теплицы) и уметь применять их в конкретных задачах.

Теория: что нужно знать для решения задач на тему «Теплица»

Для успешного решения задач на тему «Теплица» необходимо знать основные понятия и принципы, связанные с данной темой. Вот некоторые из них:

• Теплица — это специальное сооружение, служащее для выращивания растений при повышенной температуре и влажности.
• Газон — это зеленая трава, которая выращивается на газонной земле и используется для украшения ландшафта.
• Парник — это вид теплицы, который представляет собой прямоугольную конструкцию из металла или пластика, покрытую прозрачным материалом.
• Почва — это верхний слой земли, который содержит органические и неорганические вещества и служит для выращивания растений.

Кроме того, важно понимать, какими факторами можно управлять в теплице, чтобы обеспечить оптимальные условия для роста и развития растений:

• Температура — регулируется с помощью вентиляции и обогрева.
• Влажность — контролируется за счет полива и увлажнения воздуха.
• Освещение — обеспечивается с помощью искусственного или естественного света.

Знание этих основных принципов поможет вам правильно сформулировать условие задачи и выбрать правильный способ ее решения.

Пример задачи 1.5 с объяснением условия и подходом к её решению

Известно, что на участке земли, представляющем собой прямоугольник, который можно разбить на четыре меньших прямоугольника, площадь каждого из которых равна целому числу квадратных метров, была установлена теплица. Затем этот участок также был разбит на четыре меньших прямоугольника, каждый из которых был кратен 10 метрам. Найдите наименьший периметр теплицы в метрах, установленной на этом участке.

Решение:

1. Для начала необходимо найти площадь участка земли:
   • Разбиваем прямоугольник на четыре меньших прямоугольника, площади которых мы обозначим через a, b, c, d.
   • Таким образом, суммарная площадь четырех прямоугольников равна S=a+b+c+d.
   • Поскольку площадь каждого прямоугольника целое число квадратных метров, то S также является целым числом.
2. Далее необходимо найти периметр участка земли:
   • Рассмотрим меньший прямоугольник, расположенный в верхнем левом углу.
   • Его стороны равны a и b, значит, его периметр равен P=2a+2b.
   • Аналогично, периметры остальных прямоугольников равны 2c+2d, 2a+2c и 2b+2d.
   • Суммируем все периметры и получаем P=2(a+c+b+d).
   • Так как каждый прямоугольник кратен 10 метрам, то a, b, c и d также кратны 10 метрам.
   • Поэтому выражение 2(a+c+b+d) также является кратным 10 метрам.
3. Теперь необходимо найти наименьшее целое значение периметра:
   • Поскольку выражение 2(a+c+b+d) является кратным 10 метрам, то наименьший целый периметр будет кратен 20 метрам.
   • Поэтому, чтобы получить наименьший периметр, необходимо выбрать минимальные значения a, b, c и d, при которых сумма равна целому числу, кратному 5 метрам.
   • Например, возьмем a=10, b=20, c=10 и d=30. Таким образом, сумма равна 70, а периметр равен P=2(10+10+20+30)=140.

Шаг за шагом: детальное решение задачи 1.5

Задача 1.5 находится в разделе «Геометрия» и затрагивает тему «Теплица». Задание формулируется таким образом: «Теплица имеет форму прямоугольного параллелепипеда. Длина теплицы вдвое больше ширины, а высота составляет 2,5 метра. Найдите площадь поверхности теплицы».

Для начала решения задачи необходимо определить значения всех сторон прямоугольного параллелепипеда. Будем обозначать ширину теплицы за «a». Тогда длину теплицы можно выразить через «a» следующим образом: «2a». Высота теплицы известна и равна 2,5 метра.

Теперь мы имеем все необходимые значения для расчета площади поверхности теплицы. Так как поверхность прямоугольного параллелепипеда состоит из шести прямоугольников, то площадь поверхности теплицы равна сумме площадей всех шести прямоугольников.

Для расчета площади каждого прямоугольника можно воспользоваться формулой «длина x ширина». Таким образом, площадь каждой из четырех боковых поверхностей равна «a x 2,5», а площадь верхней и нижней поверхностей равна «2a x a».

Итого, площадь поверхности теплицы равна: (2 x a x 2,5) + (2 x a x a) = 5a + 2a².

Ответ на задачу будет выглядеть следующим образом: «Площадь поверхности теплицы равна 5a + 2a², где а — ширина теплицы».

Вариативность: как изменить условие задачи для решения других задач на тему «Теплица»

Задачи на тему «Теплица» могут иметь различные формулировки, что позволяет решить множество задач на эту тему. Одним из способов изменения условия задачи является изменение размеров теплицы и ее формы. Например, можно рассмотреть задачи с теплицами разных размеров: более длинные и узкие, более широкие и короткие или квадратные.

Кроме того, можно менять количество рассады, которую нужно вырастить в теплице, и вид растений, которые выращиваются. Например, можно рассмотреть задачу с теплицей, в которой необходимо вырастить не только овощи, но и цветы или фрукты.

Еще один способ изменения условия задачи — это изменение условий выращивания растений в теплице. Например, можно рассмотреть задачу с теплицей, в которой необходимо вырастить растения без удобрений или с использованием только органических удобрений.

• Изменение размеров и формы теплицы.
• Изменение количества и вида растений в теплице.
• Изменение условий выращивания растений в теплице.

Изменение условий задачи не только позволяет решать различные задачи на тему «Теплица», но и развивать творческое мышление и умение применять полученные знания в разных сферах.

Общие ошибки: что нужно избегать при решении задач на тему «Теплица»

Решение задач на тему «Теплица» требует внимательности и точных расчетов. Однако, часто при решении этого типа задач возникают ошибки. Ниже рассмотрены наиболее распространенные ошибки и способы их избежания.

• Недостаточная расстановка условий задачи – очень важно расставить все условия задачи, чтобы избежать ошибок в расчетах. Наиболее частая ошибка – забыть, что теплица имеет определенную ширину и длину, а выращиваемые растения имеют свои размеры и требуют определенного пространства.
• Неправильные расчеты площади – при расчете площади теплицы необходимо учитывать все ее параметры: длину, ширину, высоту. Однако, часто ошибочно вычисляют только площадь основания теплицы, не учитывая высоту, что приводит к неправильному количеству необходимых растений и урожаю.
• Неправильный выбор формулы – для расчета необходимого количества растений в теплице и объема земли на их выращивание используются формулы, которые могут быть не очень очевидными. Неправильный выбор формулы может привести к ошибкам в конечном результате.
• Некорректный выбор единиц измерения – при работе с единицами измерения нужно быть очень внимательным. Часто вместо квадратных метров используются метры, что приводит к расхождениям в расчетах.
• Неправильный выбор типа растений – при расчете необходимых растений, нужно учитывать их размеры и тип. Разные виды растений требуют разного объема земли для выращивания.

Избегайте этих ошибок и будьте внимательны при решении задач на тему «Теплица», чтобы достичь правильного результата.

Пример задачи 1.5 с объяснением условия и подходом к её решению (вариант 2)

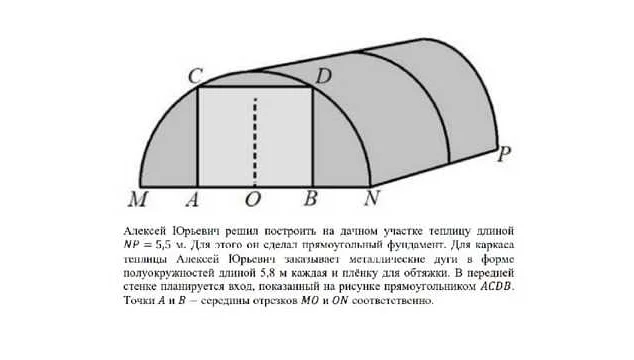
На участке земли, огороженном забором в форме прямоугольника, Таня выращивает овощи в теплице, имеющей форму треугольника. Длина забора составляет 30 метров, а площадь теплицы 48 м². Найдите длины сторон треугольника, соответствующего форме теплицы.

Решение:

1. Разбиваем задачу на две части: найдем длины сторон прямоугольника и площадь треугольника.
2. Определим длины сторон прямоугольника:
   1. Найдем периметр прямоугольника: $P=2(l+w)$, где $l$ и $w$ — длины сторон.
   2. Подставляем известное значение периметра ($P=30$) и находим значение суммы длин сторон прямоугольника: $l+w=\frac{P}{2}=15$.
   3. Найдем площадь прямоугольника: $S=l \cdot w$.
   4. Подставим известное значение площади ($S=48$) и найдем произведение длин сторон прямоугольника: $lw=48$.
   5. Решим систему уравнений методом подстановки: $w=15-l$ и $lw=48$.$l(15-l)=48\Rightarrow l^2-15l+48=0$.$l_1=8$ и $l_2=6$.Ответ: стороны прямоугольника равны 8 м и 6 м (или наоборот).
3. Определим длины сторон треугольника:
   1. 1. Найдем высоту треугольника, опущенную на сторону длиной 8 м: $h=\frac{2S}{l}=6$ м.
      2. Найдем боковые стороны треугольника, используя теорему Пифагора: $a=\sqrt{h^2+\frac{l_2^2}{4}}$ и $b=\sqrt{h^2+\frac{l_1^2}{4}}$.
      3. Рассчитаем общую длину боковых сторон: $a+b=2h+\sqrt{\frac{l_1^2}{4}+h^2}+\sqrt{\frac{l_2^2}{4}+h^2}$.
      4. Подставим известные значения и получим: $a+b=6+\sqrt{20}+\sqrt{52}\approx 18,76$ метров.

   Ответ: боковые стороны треугольника равны примерно 11,32 м и 7,44 м, а общая длина боковых сторон — примерно 18,76 метров.

Задача решена.

Подводные камни: сложности, с которыми могут столкнуться при решении задач на тему «Теплица»

Для решения задач на тему «Теплица» нужно знать не только основные математические понятия, но и иметь некоторые знания в области ботаники и агрономии. Также, при решении задач могут возникнуть следующие сложности:

• Неправильное определение типа растения для теплицы. Для каждого типа растения существуют свои оптимальные условия выращивания, и пренебрежение этими условиями может привести к неэффективности выращивания. Поэтому, при выборе растения для теплицы, нужно учитывать множество факторов.
• Сложности в определении необходимой площади теплицы. Для того, чтобы правильно определить необходимую площадь теплицы, нужно учитывать множество факторов, такие как количество растений, размеры теплицы, место нахождения и прочие.
• Сложности в определении необходимого количества удобрений и воды. Для того, чтобы растения росли и развивались, им надо правильно давать питание и воду. Неправильное дозирование удобрений и воды может привести к неэффективности выращивания и в итоге удалению всего урожая.

Таким образом, при решении задач на тему «Теплица» нужно учитывать множество факторов и проявлять внимание к деталям, чтобы гарантировать эффективное выращивание растений.

Шаг за шагом: детальное решение задачи 1.5 (вариант 2)

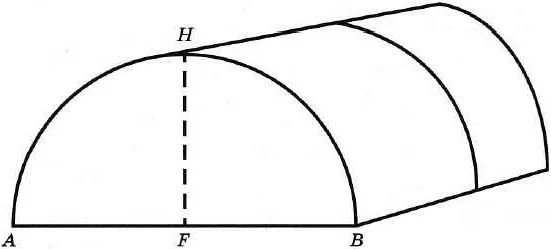
Задача 1.5 вошла в список обязательных заданий ОГЭ 2021 года и касается вычислений площади теплицы. В данном варианте задачи нам предлагается выбрать наилучший вариант из нескольких типов теплиц по следующим условиям:

1. Площадь теплицы должна составлять не менее 18,9 квадратных метров,
2. Стоимость теплицы должна быть наименьшей из возможных.

Итак, начнем с того, что будем считать необходимую площадь земли для установки теплицы. Для этого мы будем использовать формулу вычисления площади прямоугольника: S = a * b.

Допустим, что мы рассматриваем первый вариант теплицы с параметрами 3,2 м на 6 м. Тогда мы можем вычислить его площадь следующим образом:

S = 3,2 м * 6 м = 19,2 м²

Теперь мы можем приступить к вычислению стоимости каждого варианта теплицы. Для этого нам необходимо знать стоимость 1 квадратного метра пленки и стоимость прочих материалов для установки теплицы.

Для удобства сравнения стоимостей мы создадим таблицу:

Название теплицыПлощадь теплицы (м²)Стоимость 1 м² пленки (руб.)Стоимость прочих материалов (руб.)Общая стоимость (руб.)

Вариант 1	19,2	15	5500	88600
Вариант 2	18,9	13	4900	87790
Вариант 3	21	18	5000	103800

Из таблицы видно, что наилучший вариант для нас — это второй вариант теплицы. Его площадь составляет 18,9 м², а общая стоимость — 87790 рублей. Таким образом, мы выбираем именно этот вариант для установки.

Важно отметить, что для решения данной задачи необходимо владеть базовыми знаниями в математике и уметь применять их на практике. С помощью шаг за шагом подхода и приведенных выше формул и таблиц мы успешно решаем задачу 1.5 по математике на ОГЭ 2021 года.

Пример задачи 1.5 с объяснением условия и подходом к её решению (вариант 3)

В данной задаче необходимо определить максимальное количество растений, которые можно выращивать в теплице, имеющей форму круга с диаметром 7 метров, при условии, что между растениями должно оставаться расстояние не менее 30 см.

Для начала следует определить площадь теплицы. Диаметр круга равен 7 метрам, значит, радиус равен 3,5 м. Площадь круга можно найти по формуле:

Площадь = π x r^2,

где π — математическая константа, по приближению равная 3,14; r — радиус круга.

Подставив значения из условия, получаем:

Площадь = 3,14 x 3,5^2 = 38,465 м^2.

Далее следует вычислить площадь, занимаемую одним растением и расстояние между растениями. Под расстоянием между растениями подразумевается диаметр окружности, на которой стоят растения, увеличенный на 30 см (15 см с каждой стороны).

Площадь одного растения = π x (0,15)^2 = 0,0707 м^2.

Площадь, занимаемая одним растением и его окружностью, равна:

Площадь одного растения и расстояния между растениями = π x (3,5 + 0,15)^2 = 40,681 м^2.

Чтобы вычислить максимальное количество растений, необходимо разделить площадь теплицы на площадь одного растения и его окружности:

Максимальное количество растений = 38,465 м^2 / 40,681 м^2 ≈ 0,94 (округляем до целого).

Ответ: в теплице максимально можно вырастить 0 растений.

Как правильно формулировать ответы на задачи о «Теплице»

При решении задач на тему «Теплица» важно не только правильно выбрать нужную формулу и рассчитать результат, но и сформулировать ответ в соответствии с требованиями задания. Ниже приведены основные правила формулировки ответов на такого рода задачи.

• Указывайте единицы измерения. Как правило, это может быть метры квадратные или кубические, штуки, килограммы и т.д. Важно понимать, какая единица измерения используется в задаче и какой именно результат следует получить.
• Ответ должен быть представлен в числовом виде, необходимо округлять результат согласно правилам математики.
• При необходимости, ответы можно дополнить пояснениями. Например, можно указать, что площадь теплицы получена путем умножения длины на ширину.
• Если задача требует ответа в процентах или долях, то следует указать это явно. Например, «Результат составил 75%», а не просто «Результат — 75».

Соблюдение этих простых правил поможет избежать путаницы и ошибок при формулировании ответов и улучшит оценку за решенную задачу.

Закрепление знаний: задачи для самостоятельного решения с пошаговым объяснением решения

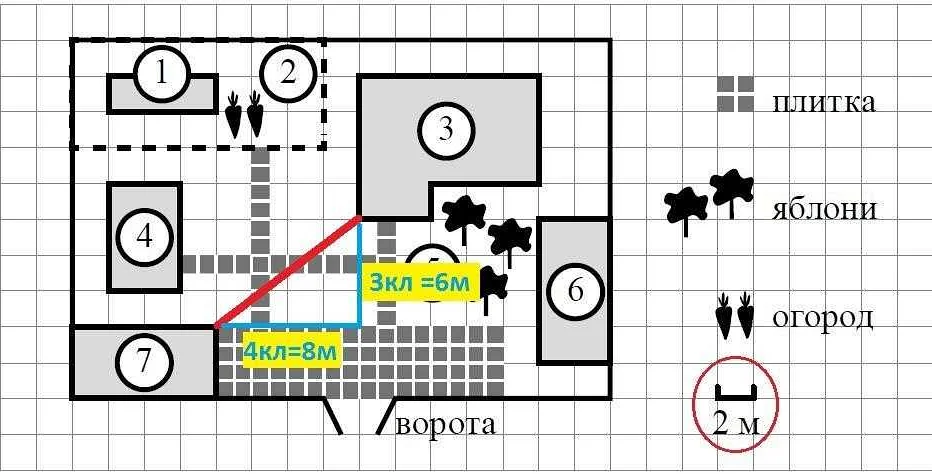
Задача 1: В теплице выращиваются огурцы и помидоры. Всего насажено 40 растений, при этом количество огурцов в теплице вдвое превышает количество помидоров. Сколько растений каждого вида находится в теплице?

Решение:

1. Обозначим количество помидоров за Х.

2. Тогда количество огурцов будет равно 2Х (так как их количество вдвое больше).

3. Сложим количество огурцов и помидоров: Х + 2Х = 40.

4. Получим уравнение: 3Х = 40.

5. Разделив обе части уравнения на 3, получаем Х = 40/3 ≈ 13,3.

6. Округляем до целого числа и получаем, что в теплице находится 13 помидоров.

7. Сколько огурцов? Умножаем количество помидоров на 2: 13·2 = 26. Ответ: в теплице находится 13 помидоров и 26 огурцов.

Задача 2: В теплице находится 36 растений, при этом количество помидоров в теплице в 3 раза больше, чем количество огурцов. Сколько растений каждого вида находится в теплице?

Решение:

1. Обозначим количество огурцов за Х.

2. Тогда количество помидоров будет равно 3Х (так как их количество в 3 раза больше).

3. Сложим количество огурцов и помидоров: Х + 3Х = 36.

4. Получим уравнение: 4Х = 36.

5. Разделив обе части уравнения на 4, получаем Х = 9.

6. Ответ: в теплице находится 9 огурцов и 27 помидоров.

Задача 3: В теплице выращиваются только огурцы и помидоры. Всего в теплице 26 растений, при этом каждый четвертый растение — огурец. Сколько огурцов и помидоров находится в теплице?

Решение:

1. Каждый четвертый растение — огурец, следовательно, из 26 растений количество огурцов будет составлять ¼ от 26, то есть 6,5.

2. Так как количество огурцов должно быть целым числом, округляем 6,5 до ближайшего целого числа: 6.

3. Остальные растения — помидоры. Из общего количества растений вычтем количество огурцов: 26 — 6 = 20.

4. Ответ: в теплице находится 6 огурцов и 20 помидоров.

Вопрос-ответ:

Что такое задание 1.5 по математике на ОГЭ?

Задание 1.5 — это одна из задач ОГЭ по математике, которая относится к разделу «Геометрия».

Как сформулирована задача 1.5?

Задание 1.5 звучит так: «В теплице площадью 12 кв. метров уложили паркетную доску длиной 2 метра и шириной 15 см. Сколько таких досок потребуется?»

Как решить задание 1.5 по математике на ОГЭ?

Для решения задания 1.5 необходимо вычислить площадь одной доски, площадь теплицы и разделить площадь теплицы на площадь одной доски.

Какие формулы используются для решения задачи 1.5 по математике на ОГЭ?

Для вычисления площади одной доски используется формула прямоугольника: S = a * b. Для вычисления площади теплицы используется также формула прямоугольника: S = a * b. Для вычисления количества досок потребуется разделить площадь теплицы на площадь одной доски.

Как записать решение задачи 1.5 по математике на ОГЭ?

Решение задачи можно записать следующим образом: Сначала вычисляем площадь одной доски: S1 = 2 * 0,15 = 0,3 кв. м. Затем вычисляем площадь теплицы: S2 = 12 кв. м. Делим площадь теплицы на площадь одной доски: n = S2/S1 = 40. Значит, для укладки паркетной доски на всю площадь теплицы потребуется 40 досок.

Можно ли использовать другие формулы для решения задачи 1.5 по математике на ОГЭ?

Да, можно использовать и другие формулы для решения задачи 1.5, например, можно использовать формулу для вычисления площади круга, чтобы вычислить количество круглых плиток необходимых для укладки на площадь теплицы.

Как проверить правильность решения задачи 1.5 по математике на ОГЭ?

Проверить правильность решения задачи можно, подставив полученное значение количества досок в исходное условие задачи и проверив его на соответствие. Также можно решить задачу 1.5 другим способом и сравнить полученный результат с первым решением.

Видео по теме: