Какие разделы математики считаются самыми сложными и почему

Статья расскажет, какие разделы математики считаются самыми сложными и почему. Читайте, чтобы узнать, какие навыки и знания требуются для понимания этих тем и как их можно изучить наилучшим образом.

Математика является одним из наиболее сложных и интеллектуальных предметов в учебной программе большинства школ и вузов. Она требует от студентов глубокого понимания и предельного внимания к деталям. Однако, есть определенные области математики, которые считаются более сложными, чем другие. Эти области могут вызывать у студентов ощущение непреодолимости и страха.

Одной из самых сложных форм математики является абстрактная алгебра. Она требует от студентов глубокого понимания теории и практики, а также умения разбираться в различных типах алгебраических структур. Но чтобы успешно преодолеть эту сложность, студентам необходимо отдавать приоритет практике и регулярному изучению материала.

Еще одной трудной областью математики является топология. Это область, которая изучает свойства форм и пространств. Она требует от студентов преодоления сложных концепций, таких как непрерывность и теория группов. Для того чтобы успешно изучить топологию, студентам необходимо ориентироваться на практику и практикуемые решения различных задач.

Как видно, математика содержит множество сложных областей, которые могут вызывать у студентов чувство беспомощности и страха. Однако, с помощью правильной системы подготовки и регулярного изучения материала, закрепления полученных знаний и применения их на практике, каждый студент сможет успешно преодолеть любые математические преграды и повысить свой интеллектуальный уровень.

Самая сложная математика и как ее преодолеть

Среди всех разделов математики, одним из самых сложных является математическая анализ, который включает в себя дифференциальное и интегральное исчисления. Эти разделы могут показаться слишком сложными для большинства студентов, но это не означает, что их нельзя понять.

Чтобы преодолеть сложности в изучении математического анализа, важно следовать нескольким простым советам. Во-первых, студентам следует посвятить достаточное количество времени на практику и повторение основных понятий. Необходимо понимать, что это требует усилий, но в результате у вас появится глубокое понимание материала.

Еще одним важным советом является постоянное общение с преподавателем и коллегами. Делитесь своими мыслями, задавайте вопросы и просите помощи в случае затруднений. Дополнительное объяснение и подсказки могут значительно улучшить уровень понимания.

• Повторяйте материал каждый день.
• Читайте дополнительную литературу.
• Решайте задачи на протяжении всего курса.
• Смотрите видеолекции и учите с помощью онлайн-курсов.
• Будьте терпеливы и не бойтесь ошибок, именно через них вы научитесь лучше.

Сложная математика не должна стать препятствием на пути к достижению ваших целей. Следуйте приведенным выше советам и вы увидите, что постепенно начнете лучше понимать и увереннее ощущать себя в этом разделе математики.

Видео по теме:

Арифметика: почему это основа, но все еще вызывает проблемы

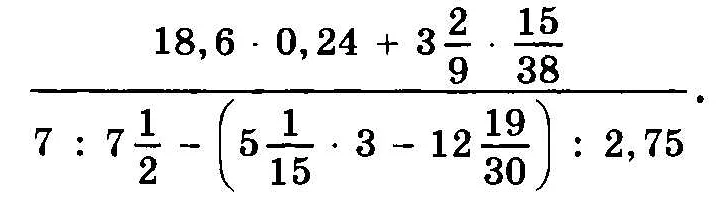
Арифметика — это одна из основных математических дисциплин, которая изучает свойства и операции над числами. Насколько бы просто это не звучало, арифметика до сих пор может вызывать проблемы у студентов любого возраста. Почему так происходит?

Одним из главных факторов, которые могут мешать пониманию арифметики, является недостаток базовых знаний… Например, не знать таблицу умножения или не понимать, как правильно округлять числа может привести к серьезным ошибкам при выполнении простых заданий. Чтобы избежать таких проблем, необходимо в первую очередь уделять внимание основам и понимать их полностью.

Еще одной причиной, почему арифметика может вызывать проблемы, является сложность задач, которые становятся все более и более сложными по мере продвижения в учебе. Они требуют от студента более глубокого понимания материала и умения применять его в разных ситуациях. Чтобы успешно справиться с такими задачами, нужно постоянно развивать свои знания и навыки в области арифметики.

Кроме того, арифметика — это не просто набор формул и правил, это основа для изучения других математических дисциплин. Понимание арифметики упрощает изучение алгебры, геометрии, тригонометрии и других областей математики. Поэтому основам арифметики стоит уделять особое внимание и не стесняться задавать вопросы по поводу того, что они не понимают.

В итоге, арифметика — это основа всей математики. Чтобы избежать проблем при ее изучении, нужно хорошо усвоить основы и понимать их полностью, постоянно развивать свои знания и не стесняться задавать вопросы.

Алгебра: простые и сложные понятия, которые нужно знать

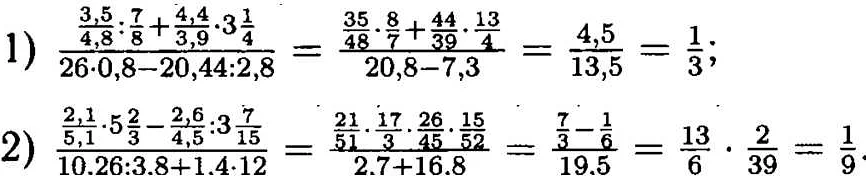
Алгебра является одним из базовых предметов в математике и обладает своими простыми и сложными понятиями, которые важно знать, чтобы успешно изучать этот предмет. Одним из самых простых понятий является понятие переменной.

Переменная является неизвестным значением, которое мы пытаемся найти в выражении. Примером такого выражения может служить x + 5 = 10. В данном случае мы пытаемся найти значение переменной x, зная, что x прибавленное к 5 равно 10. Простое, не так ли?

Однако, алгебра не ограничивается только простыми понятиями и заданиями с переменными. Очень часто нужно совершать более сложные операции, такие как умножение многочленов, решение систем уравнений или даже определитель матрицы.

Для успешного изучения алгебры существует несколько правил. Во-первых, необходимы терпение и настойчивость. Некоторые задания могут занять много времени и усилий, но их решение приблизит к пониманию материала. Во-вторых, нужно строить на знаниях постепенно. Изучение более сложных тем следует начинать только после успешного освоения более простых концепций. В-третьих, нужно готовиться к работе над заданиями. Изучение алгебры не происходит только в классе, поэтому важно уделить достаточно времени на выполнение домашних заданий, повторение материала и самостоятельное изучение.

1. Переменная — неизвестное значение
2. Терпение и настойчивость необходимы для успешного изучения алгебры
3. Строй на знаниях постепенно
4. Готовься к работе над заданиями

Вопрос-ответ:

Какая математика считается самой сложной для изучения?

Самой сложной для изучения математикой можно считать абстрактную алгебру, теорию чисел, топологию, математическую логику, теорию меры и интеграла, дифференциальную геометрию, алгебраическую геометрию и функциональный анализ. Все эти разделы математики являются достаточно сложными и требуют глубокого понимания математических концепций, что может потребовать многолетнего обучения.

Какова причина того, что некоторые разделы математики являются более сложными, чем другие?

Причин может быть несколько. Например, некоторые разделы математики содержат большое количество абстрактных понятий и теорем, которые сложно понять и запомнить. Кроме того, некоторые разделы математики связаны с другими областями науки, такими как физика и информатика, и требуют дополнительной подготовки и знаний из этих областей.

Есть ли способы упрощения изучения сложных математических разделов?

Да, есть. Один из способов — это постепенное изучение материала и разбиение его на более мелкие части. Необходимо начинать с простых понятий и теорем, затем постепенно переходить к более сложным. Еще один способ — это изучение материала вместе с другими студентами или преподавателями, что может помочь в понимании математических концепций и их применения в реальной жизни.

Какие навыки необходимо развить для успешного изучения сложных математических разделов?

Для успешного изучения сложных математических разделов необходимо развить логическое мышление, умение анализировать проблему и находить ее решение. Кроме того, важно иметь навыки работы с формулами и графиками, а также умение изображать абстрактные концепции. Знание и понимание математических основ и теорий также является важным фактором для успешного изучения сложных разделов математики.

Каковы преимущества изучения сложных математических разделов?

Изучение сложных математических разделов может помочь развить умение решать проблемы, анализировать информацию и принимать решения. Эти навыки могут быть полезны и в личной жизни, и на работе. Кроме того, знание сложных математических концепций может дать возможность работать в определенных областях, таких как физика, информатика, экономика, статистика и многие другие.

Каким образом можно применять знания, полученные из сложных математических разделов, в реальной жизни?

Знания, полученные из сложных математических разделов, могут быть применены в различных областях, таких как физика, инженерия, информатика, экономика, медицина и многие другие. Например, знание математических концепций может помочь спроектировать новое устройство, вычислить оптимальную дозу лекарства для пациента, разработать новый алгоритм для уменьшения времени обработки данных и многое другое.

Каким образом можно подготовиться к изучению сложных математических разделов?

Для того чтобы подготовиться к изучению сложных математических разделов, необходимо иметь хорошее математическое образование и знание базовых математических концепций. Рекомендуется также обратиться к специализированным учебникам и ресурсам в Интернете, посетить курсы и лекции, связанные с интересующим разделом математики. Необходимо также не бояться задавать вопросы и общаться с другими студентами и преподавателями.

Геометрия: изучаемые формулы и почему они вызывают трудности

Геометрия — это раздел математики, изучающий пространственные фигуры и их свойства. Одним из основных способов описания геометрических фигур являются формулы, которые описывают их геометрические параметры. Изучение формул является неотъемлемой частью изучения геометрии.

Однако для многих учеников геометрические формулы могут вызывать трудности. Это может быть связано с тем, что формулы могут быть сложными и запоминаются не так легко, как числовые факты. Также некоторые ученики могут испытывать трудности в понимании геометрических понятий, которые являются основой для получения формул.

Для преодоления трудностей в изучении геометрии и формул стоит обратить внимание на ряд факторов, которые могут облегчить изучение материала. Один из таких факторов — это выполнение практических заданий, которые помогают визуализировать геометрические понятия и формулы. Также рекомендуется использовать таблицы с формулами и примерами по каждому типу геометрических фигур для лучшего запоминания материала.

Важно также помнить, что геометрия является разделом математики, который требует постоянного изучения и тренировки. Постепенное укрепление базовых знаний и общего уровня математической грамотности поможет ученикам более легко усваивать формулы и понимать основы геометрии.

Тригонометрия: как рассчитывать углы и стороны треугольников

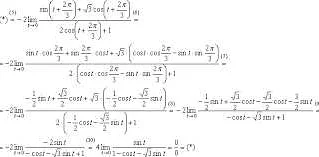
Тригонометрия — это раздел математики, который изучает связь между углами и сторонами треугольников. Знание тригонометрии очень важно для решения задач в различных областях науки и техники.

Основными понятиями в тригонометрии являются синус, косинус и тангенс угла. Синус угла определяется как отношение противоположной стороны к гипотенузе, косинус угла — как отношение прилежащей стороны к гипотенузе, а тангенс угла — как отношение противоположной стороны к прилежащей.

Тригонометрические функции используются для решения задач на вычисление углов и сторон треугольников. Их значения можно найти в таблицах тригонометрических функций или вычислить с помощью калькулятора.

Чтобы решить задачу на вычисление углов и сторон треугольников, необходимо использовать теорему Пифагора, правила синусов и косинусов, тангенсов и котангенсов. Также необходимо уметь переводить меру угла из градусов в радианы и наоборот.

Основы тригонометрии — это не только вычисления, но и графическое представление тригонометрических функций на координатной плоскости. Графики функций синуса, косинуса и тангенса имеют особенности, которые нужно уметь определять и интерпретировать.

Хорошее понимание тригонометрии поможет не только в учебе, но и в решении практических задач связанных с построением и расчетом космических кораблей, зданий, поверхности земли и многих других объектов.

Калькул: что это и почему многие находят его сложным

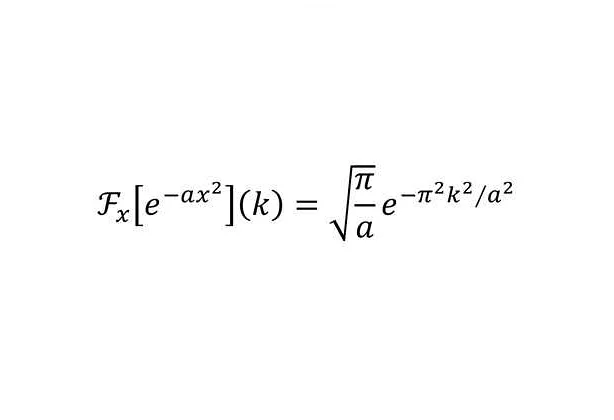
Калькул, или математический анализ, — это раздел математики, который изучает изменение их свойств математических объектов. Он включает в себя дифференциальное и интегральное исчисление, а также теорию функций. Большинство людей считают калькул самым сложным уровнем математической дисциплины из-за его высокой абстрактности и необычных концепций.

Одним из различий между калькулом и другими областями математики является наличие многих понятий и терминов, которые нельзя понять, просто изучив их определения. Например, понимание понятия предела, являющегося одним из ключевых в калькуле, требует не только понимания его определения, но и практических навыков решать сложные примеры.

Преодоление трудностей в калькуле требует сочетания теоретического обучения и практической работы. Стоит уделить время пониманию основных концепций и определений, а также регулярной практике и решению множества задач и упражнений. Важно не только использовать формулы и решения примеров, но и находить методы решения сложных задач, чтобы улучшить свои навыки и предметное понимание.

Калькул может быть сложным материалом для изучения, однако с правильным подходом и усердной работой, он станет весьма интересным и расскажет об истинной красоте математической науки.

Дифференциальные уравнения: что они означают и как с ними работать

Дифференциальное уравнение – это уравнение, в котором неизвестной функцией является функция, зависящая от одной или нескольких переменных, и ее производные. Таким образом, дифференциальное уравнение – это уравнение, связывающее функцию и ее производные.

Решение дифференциальных уравнений может быть очень сложным и требует знаний высшей математики. Однако, некоторые простые дифференциальные уравнения можно решить без использования специальных методов.

Примеры дифференциальных уравнений:

• y’ = x
• y» + 3y’ – 4y = 0
• u»’ + 2u» – 5u’ + 3u = 0

Для решения дифференциальных уравнений используются различные методы, такие как методы разделения переменных, метод вариации постоянной, метод Лапласа, метод Эйлера и другие. Некоторые уравнения могут быть решены с помощью численных методов, таких как метод Эйлера, метод Рунге-Кутты и метод простых итераций.

Однако при решении дифференциальных уравнений необходимо быть внимательными и не допускать ошибок, так как даже небольшая ошибка может привести к неверному результату.

Также, решение дифференциальных уравнений является важным элементом в научных и технических расчётах, так как они позволяют описывать многие процессы, такие как теплопроводность, динамика жидкости и многие другие.

Статистика: как интерпретировать и анализировать данные

Статистика является одним из важнейших инструментов при анализе данных. Интерпретация и анализ данных является ключевой задачей для большинства компаний и организаций. Чтобы правильно понимать и использовать данные, нужно иметь навыки статистического анализа.

Для начала нужно понимать, что есть два основных типа данных: количественные и категориальные. Количественные данные выражаются числами, а категориальные данные — категориями или метками.

Кроме того, нужно уметь оценить различные параметры, такие как среднее значение, дисперсию, медиану, а также проверять статистические гипотезы. Для этого можно использовать статистические пакеты программного обеспечения, такие как R или SPSS.

Для наглядной интерпретации данных часто используются графики. Они позволяют наглядно представить данные и быстро выявить особенности, такие как тренды или выбросы.

Важно также учитывать контекст данных и не делать поспешных выводов. Необходимо проводить тщательный анализ данных и учитывать их источник.

В современном мире очень много данных, и умение анализировать и интерпретировать их является важным навыком для бизнеса и науки. Обучение статистике поможет не только лучше понимать данные, но и принимать более обоснованные решения.

Теория вероятности: как рассчитываются шансы и возможности

Теория вероятности – это раздел математики, который изучает случайные явления и позволяет предсказывать вероятность их возникновения. Если говорить простым языком, то теория вероятности помогает рассчитать шансы на то, что то или иное событие произойдет.

Основным понятием теории вероятности является вероятность – это число, которое характеризует степень возможности наступления того или иного события. Вероятность выражается числом от 0 до 1, где 0 означает, что событие не произойдет, а 1 – что произойдет.

Для рассчета вероятности используются специальные формулы и методы. Одним из основных является формула классической вероятности, которая основывается на предположении, что все элементарные исходы равновозможны.

• Пример 1: если в мешке имеется 5 разных мячей, из которых 3 – белые, а 2 – черные, то вероятность вытащить белый мяч равна 3/5 или 0,6.
• Пример 2: если у вас есть 2 монеты, то вероятность выпадения орла на обеих монетах одновременно составляет 0,5 * 0,5 = 0,25 (или 25%).

Кроме классической вероятности, существуют также статистическая (базируется на наблюдении за частотой событий в прошлом) и субъективная (основанная на сугубо личных оценках и убеждениях).

Важно понимать, что теория вероятности не дает абсолютной гарантии наступления того или иного события – она лишь рассчитывает степень его вероятности. Однако, знание теории вероятности может помочь в принятии различных решений и прогнозировании будущих событий.

Логика: применение математической логики в различных областях

Математическая логика — это раздел математики, который исследует формальные методы вывода и анализа доказательств. Она является основой для многих областей знаний, таких как философия, информатика, теория алгоритмов, искусственный интеллект и т. д.

В философии математическая логика применяется для анализа аргументации и доказательств, что помогает выявить ошибки в рассуждениях и улучшить качество мышления. В информатике математическая логика используется для разработки алгоритмов и программного обеспечения.

Теория алгоритмов основана на идеях математической логики и позволяет рассматривать различные проблемы вычислительной сложности. Искусственный интеллект также требует знаний в области математической логики для создания различных моделей и алгоритмов.

Таким образом, знание математической логики является важным для решения различных задач в различных областях. Для улучшения своих навыков в этой области рекомендуется изучать теорию и решать практические задачи, используя различные математические методы и инструменты.