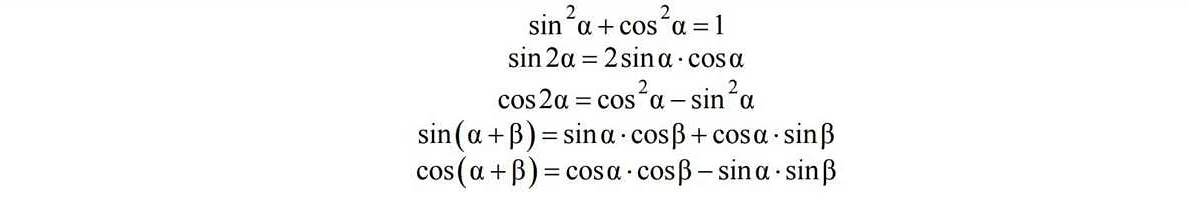Какие темы и задания по математике профиль ожидают на ЕГЭ: подробный анализ материалов и рекомендации

Узнайте, какие материалы входят в программу ЕГЭ по математике профиль. В статье представлены подробные сведения о темах, которые будут проверяться на экзамене, и рекомендации по подготовке к ним. Получите полезные советы и увеличьте свои шансы на успешное сдачу ЕГЭ по математике профиль.

Единой государственной экзаменации (ЕГЭ) по математике подвергается огромное количество школьников в России. В частности, для профильного уровня экзамен предназначен для школьников, которые собираются поступать в вузы на технические специальности и хотят получить глубокие знания по математике.

На ЕГЭ по математике профильного уровня, школьники должны демонстрировать знания не только по алгебре и геометрии, но и умения решать сложные задачи, использовать преобразования, разбираться в тригонометрии и математической логике. При этом нужно учитывать, что задачи на ЕГЭ по математике могут быть оформлены в различных форматах, включая текст, графики, таблицы и т.д.

Для успешной сдачи ЕГЭ по математике профильного уровня, школьникам необходимо углубленное знание математических основ, понимание геометрических и аналитических преобразований, умение решать задачи с использованием знаний из различных разделов математики и применять полученные знания на практике.

Математика на ЕГЭ: основные темы и материалы

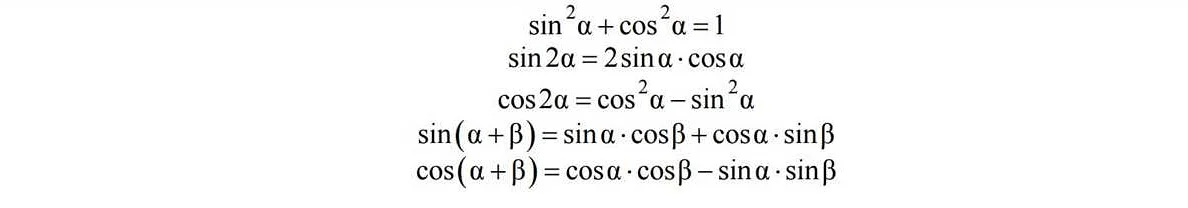
ЕГЭ по математике является одним из самых важных экзаменов для выпускников школ. В 2021 году он будет проводиться в офлайн формате, но это не меняет того факта, что необходимо тщательно подготовиться к этому экзамену.

Основные темы, которые будут рассматриваться на ЕГЭ по математике, включают в себя: арифметические операции, геометрию, алгебру, функции, тригонометрию, вероятность и статистику. В рамках каждой из этих тем есть определенные материалы, которые необходимо изучить.

Например, для геометрии нужно знать основные теоремы и формулы, такие как теорема Пифагора, формулы площадей и объемов, углы, прямые и плоскости. Для алгебры нужно знать, как решать уравнения, строить графики функций, использовать формулы сумм, произведений и степеней.

Для успешной подготовки к ЕГЭ по математике также полезно изучить прошлые тесты и пройти множество практических заданий, которые помогут понять, как формулируются вопросы и как на них отвечать. Важно запоминать формулы и уметь применять их в конкретных задачах, а также находить ошибки и проверять свои решения на правильность.

Важно не забывать о взаимосвязи между различными темами математики, например между алгеброй и геометрией, что может помочь решить сложные задачи. Чем больше ученик практикуется и отрабатывает навыки, тем больше шансов на успешный результат на ЕГЭ по математике.

Видео по теме:

Алгебра

Алгебра – один из основных разделов математики и один из самых важных предметов на ЕГЭ по математике. Её изучение включает в себя анализ функций, системы уравнений, матрицы, тригонометрию и др. Также в алгебре активно используется символическое и логическое мышление.

Для успешной сдачи ЕГЭ по алгебре необходимо хорошо знать все темы, в том числе: разложение на множители, системы уравнений, решение уравнений, теорию функций, матрицы, арифметические и геометрические прогрессии и т.д.

На ЕГЭ по математике предусмотрено много задач, в которых требуется применять знания из алгебры. Эти задачи могут быть как относительно простыми, так и сложными, так что рекомендуется не ограничиваться поверхностным изучением темы, а уделять этому разделу математики максимум времени и внимания, чтобы быть готовым к решению любых задач, которые могут быть предложены на ЕГЭ по математике.

• Разложение на множители – может быть использовано для упрощения сложных алгебраических выражений. Это важное знание в алгебре, которое может помочь сделать решение задач более эффективным;
• Матрицы – используются для решения систем линейных уравнений. Это важное и практическое знание в алгебре, которое может быть применено во многих областях;
• Теория функций – знание о теории функций позволяет понимать свойства различных видов функций и анализировать их графики. Это, в свою очередь, помогает при решении задач на нахождение координат точек пересечения графиков функций;
• Геометрические прогрессии – это видецессии, которая встречается в задачах на математику и физику. Понимание их особенностей и формул поможет легче решать подобные задачи;

Геометрия

Геометрия является одним из основных разделов математики, который включает в себя изучение фигур, пространственных отношений между ними и их свойств. В рамках ЕГЭ по математике профиль можно ожидать задания по геометрии различной сложности.

Одной из ключевых тем в геометрии является изучение треугольников — их свойств, видов и признаков. Для решения задач на треугольники важно знать основные теоремы и формулы, а также уметь применять их на практике.

Кроме того, на ЕГЭ можно встретить задания по геометрии в пространстве, включающие в себя понимание основных понятий — расстояние, углы, плоскости, прямые и т.д. Также важно иметь представление о проекциях точек и фигур на плоскости.

В целом, для успешного решения задач по геометрии на ЕГЭ необходимо не только знать теорию и формулы, но и уметь применять их в практических ситуациях, а также английские термины, чтобы правильно понимать условия заданий.

Вопрос-ответ:

Какие темы будут включены в материалы ЕГЭ по математике профильного уровня?

В ЕГЭ по математике профильного уровня будут включены следующие темы: алгебра и начала математического анализа. В алгебре будут задания по работе с многочленами, системами линейных уравнений, графиками, тригонометрическими функциями и другими темами. В началах математического анализа будут задания на дифференциальное и интегральное исчисление, теорию вероятности и статистику и др.

Каков уровень сложности заданий ЕГЭ по математике профильного уровня?

Уровень сложности заданий ЕГЭ по математике профильного уровня высокий, он направлен на проверку глубоких знаний и умения применять их на практике. Задания содержат нестандартные ситуации и требуют аналитического мышления и логического подхода к решению. Однако, ученики, которые подготовятся к ЕГЭ, будут готовы к сдаче и получат высокие баллы.

Какие математические знания необходимо знать для успешной сдачи ЕГЭ по математике профильного уровня?

Для успешной сдачи ЕГЭ по математике профильного уровня необходимы знания по алгебре и началам математического анализа. Студенты должны знать и уметь применять все основные формулы, теоремы и правила алгебры и математического анализа, а также уметь решать сложные задачи на их основе. Ученики также должны уметь работать с графиками, таблицами и диаграммами для решения заданий по статистике и теории вероятности.

Как лучше готовиться к ЕГЭ по математике профильного уровня?

Для успешной подготовки к ЕГЭ по математике профильного уровня необходимо правильно распределить свое время на изучение теоретического материала и решение практических задач. Важно заниматься регулярно, уделяя достаточное количество времени на подготовку каждому блоку заданий. Дополнительно можно использовать учебники, тесты, работать с практическими задачами и привлекать учителей для проверки решения.

Какие математические навыки помогут сдать ЕГЭ по математике профильного уровня на высокий балл?

Для успешной сдачи ЕГЭ по математике профильного уровня на высокий балл необходимо иметь хорошие знания по всем разделам математики, а также уметь применять их на практике. Важно уметь анализировать информацию, работать с математическими формулами и графиками, решать сложные задачи и контролировать свою работу. Знание английского языка также может помочь со сдачей ЕГЭ по математике на высокий балл в связи с возможностью работать с иностранными источниками математических знаний.

Как узнать, что я имею достаточные знания для сдачи ЕГЭ по математике профильного уровня на хороший балл?

Для того чтобы узнать, что у вас достаточные знания для сдачи ЕГЭ по математике профильного уровня на хороший балл, необходимо провести тестирование своих знаний. Важно правильно выбрать тест, определив свой уровень подготовки, и тщательно проработать его. Только после этого можно понимать, какие знания нужно еще усовершенствовать, чтобы сдать экзамен на высокий балл и какие методы и приемы следует использовать при подготовке.

Какие ошибки нужно избегать при подготовке к ЕГЭ по математике профильного уровня?

Важно избегать прокрастинации, т.е. откладывания занятий на потом, и наоборот, регулярно заниматься математикой. Не рекомендуется изучать материал поверхностно, не понимая сути и принципов, по которым он работает. Также нужно избегать рутинного повторения учебников и заданий, которые уже решали ранее. Нужно активно использовать помощь учителей и репетиторов, изучать новые методы, которые могут помочь решить сложные математические задачи.

Математический анализ

Математический анализ — это важная часть программы ЕГЭ по математике. Она охватывает такие темы, как производные, интегралы, функции и прочее.

Важно продолжать усовершенствовать свои знания в математическом анализе, чтобы успешно сдать ЕГЭ. Это включает изучение различных методов нахождения производных и интегралов, анализ функций и их графиков, умение решать задачи на определение максимумов и минимумов функций и т.д.

Помимо этого, часто в заданиях ЕГЭ по математике рассматриваются понятия пределов и рядов. Поэтому также важно отработать умение вычислять пределы, понимать и использовать ряды и функциональные последовательности.

Хорошей практикой является решение задач и экзаменационных билетов по математическому анализу. Это поможет ознакомиться с типичными заданиями ЕГЭ.

Теория вероятностей и математическая статистика

Как правило, на ЕГЭ по математике профильного уровня могут быть поставлены задачи, связанные с теорией вероятностей и математической статистикой. Эти две темы очень тесно связаны и играют важную роль во многих науках и областях жизни.

Теория вероятностей — это раздел математики, изучающий вероятности тех или иных явлений и событий. Она широко применяется в финансовых, промышленных и научных кругах, например, для прогнозирования рисков в бизнесе, определения безопасности авиаперевозок, составления шансов на выигрыш в лотерее и т.д.

Математическая статистика — это еще один раздел математики, который занимается методами сбора, анализа и интерпретации данных. Важно именно понимание основных понятий и методов, поскольку без этого трудно составить качественный математический анализ и сделать обоснованный вывод.

Студенты, которые готовятся к ЕГЭ по математике, должны овладеть основной теорией и понимать, как применять ее на практике. При решении задач по теории вероятностей и математической статистике необходимо учитывать все условия задачи, сверять свой ответ с возможными вариантами и не забывать, что даже маленькая ошибка может привести к неправильному результату.

Эти две темы являются одними из самых сложных и объемных в математике, поэтому необходимо уделять достаточно времени для их усвоения и закрепления. Однако, благодаря правильной подготовке, студенты смогут успешно справиться с заданиями на ЕГЭ по математике и достичь высоких результатов.

Комбинаторика

Комбинаторика — раздел математики, изучающий задачи выбора и расположения объектов, состоящих из отдельных элементов. Она используется в различных областях, например, в теории вероятностей, информатике, экономике, физике, биологии и других.

К числу основных понятий комбинаторики относятся перестановки, размещения и сочетания. Перестановка — это упорядоченная выборка объектов, размещение — выборка и расположение объектов в определенном порядке, а сочетание — выборка объектов, при которой порядок не учитывается.

Комбинаторика также связана с теорией графов и теорией игр. Она помогает решать задачи из области оптимизации, поиска оптимальных стратегий, оценивания шансов на успех и других.

Для успешной подготовки к ЕГЭ по математике необходимо изучить базовые понятия и приемы работы с ними, уметь применять их в разных задачах и быть готовым к решению задач по комбинаторике на экзамене.

Тригонометрия

Тригонометрия – раздел математики, изучающий соотношения между углами и сторонами прямоугольных треугольников, а также свойства тригонометрических функций. На ЕГЭ по математике профиль часто встречаются задачи, связанные с тригонометрией.

Одной из основных тригонометрических функций является синус. Она определяется как отношение противолежащего катета к гипотенузе треугольника. На ЕГЭ часто встречаются задачи, где необходимо находить значение синуса угла или определять угол по заданному значению синуса.

Кроме синуса, на ЕГЭ также могут встречаться задачи по косинусу, тангенсу, котангенсу и другим тригонометрическим функциям. Важно понимать их определения и свойства, а также уметь использовать формулы перевода из одной тригонометрической функции в другую.

Тригонометрия может использоваться для решения задач в различных областях, например, в геометрии, физике, экономике и др. Поэтому знание тригонометрии может быть полезным как для сдачи ЕГЭ, так и для последующей жизни.

Функции

Функция – математический объект, который отображает одно множество (называемое областью определения) на другое множество (называемое областью значения). Функции присутствуют в огромном количестве областей науки, техники, экономики, бизнеса, и т.д.

В контексте ЕГЭ по математике функции — это одна из самых важных тем, которые будут рассмотрены. При подготовке к экзамену важно знать определения функций, виды функций, основные свойства и графики функций.

• Определения функции:
  • Функция является математическим объектом, возникающим при сопоставлении каждому элементу из одного множества соответствующего элемента из другого множества.
  • Отображение, при котором каждому числу из определенного множества (области определения) соответствует единственное число из другого множества (области значений).
• Виды функций:
  • Линейная функция.
  • Квадратичная функция.
  • Степенная функция.
  • Тригонометрические функции.
  • Логарифмические и показательные функции.
• Основные свойства функций:
  • Область определения функции.
  • Область значений функции.
  • Нули функции.
  • Монотонность функции.
• Графики функций:
  • Линейная функция – прямая линия.
  • Квадратичная функция – парабола.
  • Степенная функция – кривая.

Важно помнить, что функции – одна из важнейших тем на ЕГЭ по математике. Хорошее понимание функций и их свойств поможет решить многие задачи, которые будут представлены на экзамене.

Уравнения и неравенства

Уравнения и неравенства являются одной из основных тем математики, изучаемых на уроках и проверяемых на ЕГЭ. Умение решать их может помочь не только в повседневной жизни, но и при прохождении тестов и экзаменов.

Уравнение — это математическое выражение, в котором значением переменной является число, при котором обе части уравнения равны. Решение уравнения — это такое значение переменной, при котором обе части уравнения равны между собой.

Неравенство — это математическое выражение, в котором используется знак неравенства. Если два числа не равны между собой, то можно определить, какое из них больше или меньше. Решение неравенства — это множество значений переменной, при которых неравенство выполнено.

Для решения уравнений и неравенств необходимо знание различных методов и приемов, которые включают в себя подстановку, приведение подобных членов, факторизацию и другие. Также важным является умение составлять и решать системы уравнений и неравенств.

На ЕГЭ можно ожидать заданий на решение простых и сложных уравнений, неравенств и систем уравнений и неравенств. При выполнении заданий необходимо использовать логическое мышление, оперировать алгебраическими приемами и уметь правильно интерпретировать полученный результат.

Матрицы

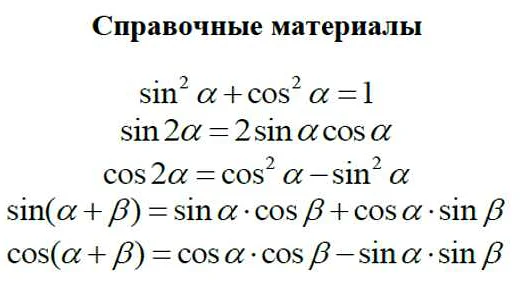
Матрица – это таблица чисел, состоящая из строк и столбцов. Она используется в математике для решения систем линейных уравнений, а также для описания преобразований в геометрии и физике.

Матрицы можно складывать, вычитать, умножать и транспонировать. Умножение матриц осуществляется по определенному правилу, которое следует запомнить. Также для матриц определены инверсии и определители.

Матрицы и ЕГЭ

• На ЕГЭ по математике обязательно встретятся задания на нахождение определителя матрицы и ее инверсии.
• Задания могут быть связаны с произведением матриц или расстановкой чисел по матрице.
• Важно уметь работать с матрицами на практике: умножать, складывать, транспонировать.

Советы по подготовке

1. Выписывайте основные формулы и правила умножения матриц – это поможет запомнить их.
2. Решайте задачи по матрицам на тренировочных ЕГЭ и контрольных работах – это поможет проверить свои знания.
3. Проверяйте свои вычисления и не забывайте учитывать условия задачи.

Дифференциальные уравнения

Дифференциальные уравнения являются одной из важнейших разделов математики, который широко используется в различных областях знания, таких как физика, химия, биология и др. Дифференциальное уравнение — это уравнение, которое содержит производную или производные функции (неизвестной переменной). Решение уравнения представляет собой нахождение такой функции, которая удовлетворяет данному уравнению.

На ЕГЭ по математике профиль можно ожидать задания на решение дифференциальных уравнений первого порядка, а также интегрирующих множителей, с точной формулой и методом Эйлера, задачи на решение уравнений второго порядка с постоянными коэффициентами, задачи на построение дифференциального уравнения по заданным условиям и т.д.

Чтобы успешно справиться с заданиями по дифференциальным уравнениям, необходимо хорошо знать свойства производных и интегралов, уметь решать линейные уравнения, а также уметь анализировать графики функций. Кроме того, важно уметь применять соответствующие методы решения уравнений в зависимости от их типа и заданных условий.

На ЕГЭ по математике профиль можно ожидать как базовые задания, так и задания повышенной сложности на дифференциальные уравнения. Поэтому важно использовать все доступные источники для подготовки и тренировки перед экзаменом, включая учебники, задания и тесты, тренажеры, курсы и занятия с преподавателем, а также обратиться за помощью к более опытным студентам или учителям по математике.

Задания с применением аналитической геометрии

Аналитическая геометрия является одним из наиболее важных разделов математики. На ЕГЭ по математике можно ожидать заданий с применением этой дисциплины.

В заданиях на ЕГЭ по математике могут храниться вопросы о построении графиков функций, анализе уравнений прямых и плоскостей, а также о решении задач на дистанции и углы между прямыми и плоскостями.

Чтобы успешно справиться с заданиями по аналитической геометрии, необходимо хорошо знать свойства прямых и плоскостей, уметь решать уравнения и преобразовывать их формы, а также знать основы работы с матрицами и определителями.

Существует множество учебников и пособий по аналитической геометрии, которые помогут лучше понять принцип работы с заданиями ЕГЭ по математике. Кроме того, подготовиться к экзамену помогут специальные тренировочные задания, которые можно найти в интернете или приобрести в библиотеке.

Наконец, одним из главных методов подготовки к заданиям ЕГЭ по математике является выполнение множества практических заданий, чтобы понять, как применять теорию на практике.