Когда в математике

Когда в математике — это понятие, которое обозначает наступление определенного условия или события в рамках математической задачи или модели. Узнайте, как и когда использовать это понятие в различных математических контекстах и примерах.

Математика — это один из самых важных предметов, который помогает развивать логическое мышление и умение решать сложные задачи. В математике существует множество правил и условий, которые необходимо знать, чтобы успешно решать задачи и находить правильные ответы.

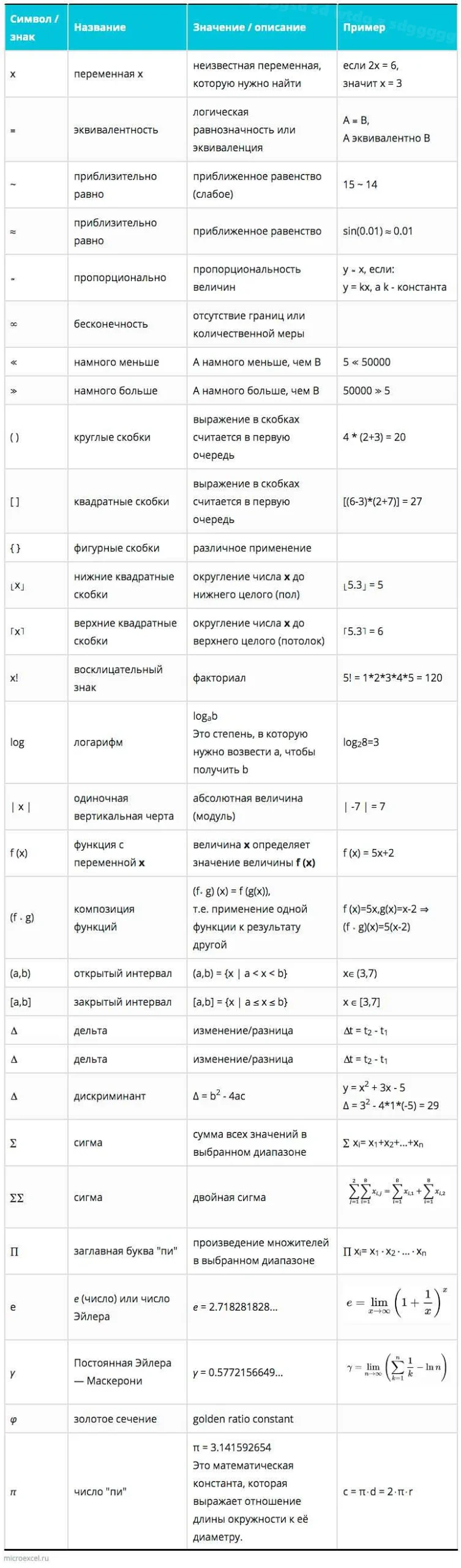
Условия в математике:

1. Уравнение — это математическое выражение, в котором присутствует знак равенства и неизвестная переменная. Для решения уравнения необходимо найти значение этой переменной, которое удовлетворяет заданным условиям.

2. Неравенство — это математическое выражение, в котором присутствуют знаки больше или меньше. Неравенство показывает отношение между двумя значениями. Например, x < 5 означает, что значение переменной x меньше 5.

3. Система уравнений — это набор уравнений, которые должны выполняться одновременно. Решение системы уравнений — это такие значения переменных, которые удовлетворяют всем уравнениям системы.

Основные примеры задач, в которых применяются условия:

• Решение уравнений и неравенств.
• Решение задач на нахождение неизвестных.
• Решение систем уравнений.
• Задачи на пропорциональность.

Понимание и применение условий в математике поможет вам находить правильные решения и достигать успеха в изучении этого предмета.

Что такое «Когда в математике»

Вместо того, чтобы просто запоминать формулы и правила, ученики могут решать задачи, связанные с конкретными ситуациями. Например, они могут решать задачи о времени, расстоянии, долях и процентах, используя знания, полученные в процессе изучения математики.

Такой подход позволяет ученикам более глубоко понять математические понятия и их применение в реальной жизни. Они могут видеть, как математика применяется в повседневных ситуациях и, таким образом, лучше усваивать материал.

Кроме того, «Когда в математике» позволяет ученикам развивать свои навыки анализа, логического мышления и проблемного мышления. Они учатся анализировать ситуации, выделять ключевые данные, формулировать гипотезы и проверять их с помощью математических методов.

В итоге, «Когда в математике» помогает ученикам не только освоить математику, но и развить навыки, которые могут быть полезными в жизни и образовании. Они учатся решать проблемы, анализировать информацию и применять математические методы в различных ситуациях.

Основные условия

Для успешного изучения математики необходимо запомнить и понять несколько основных условий:

1.	Правило четырех действий: сложение, вычитание, умножение и деление.
2.	Знание основных математических операций: сложение, вычитание, умножение и деление чисел.
3.	Понимание понятий и определений, таких как числа, функции, графики и т. д.
4.	Умение решать математические задачи и применять полученные знания на практике.
5.	Точность и внимательность при работе с числами и символами.

Эти основные условия помогут вам освоить математику и использовать ее в реальной жизни.

Условие 1: Как определить «Когда в математике»

Чтобы определить «Когда в математике», необходимо внимательно прочитать условие задачи и обратить внимание на ключевые слова или фразы, которые указывают на определенное время или условие. Эти ключевые слова или фразы могут быть разными в зависимости от типа задачи или математической операции, которую необходимо выполнить.

Например, если задача говорит: «Когда в математике сумма двух чисел равна 10», это означает, что мы должны найти все возможные комбинации чисел, которые в сумме дают 10. В этом случае мы ищем все «когда» или условия, при которых выполняется данное уравнение.

Важно отметить, что «Когда в математике» может быть связано с различными математическими операциями, такими как сложение, вычитание, умножение, деление, степени и корни. Кроме того, «Когда в математике» может относиться к разным областям математики, таким как алгебра, геометрия, тригонометрия, вероятность и статистика.

Поэтому, чтобы успешно решать математические задачи, необходимо уметь определить «Когда в математике» и использовать соответствующие методы и подходы для решения задач в различных условиях.

Условие 2: Как применить «Когда в математике»

Условие “Когда в математике” используется для определения момента, когда определенное действие должно быть выполнено. Оно позволяет упростить решение различных задач и применять математические методы наиболее эффективным образом.

Пример: Когда в математике нужно найти сумму двух чисел, необходимо сложить эти числа и получить итоговую сумму. Это условие позволяет нам точно определить, когда следует применять операцию сложения.

Применение условия «Когда в математике» помогает упростить решение задач и повысить эффективность математических операций. Оно является одним из ключевых элементов успешного использования математики в повседневной жизни и научно-исследовательской деятельности.

Условие 3: Когда использовать «Когда в математике»

Когда в математике вам необходимо выразить условие или ситуацию, которая может быть представлена в виде математических формул или операций, вы можете использовать конструкцию «Когда в математике». Эта конструкция поможет вам уточнить контекст и сформулировать вашу мысль более точно и понятно.

Например, если вы хотите описать ситуацию, когда происходит сложение двух чисел, вы можете написать: «Когда в математике нужно сложить два числа, используется операция сложения». Здесь конструкция «Когда в математике» указывает на условие, при котором применяется операция сложения.

Также «Когда в математике» может быть использовано для описания особых случаев или исключений. Например, «Когда в математике встречается деление на ноль, результат равен бесконечности». В этом случае конструкция «Когда в математике» указывает на условие, при котором происходит деление на ноль и результатом является бесконечность.

Использование конструкции «Когда в математике» помогает уточнить контекст и сделать ваше объяснение более понятным и четким. Это особенно полезно при обучении математике или при написании математических текстов и учебных материалов.

Важно помнить, что конструкция «Когда в математике» следует использовать только в математическом контексте и не применять ее в других областях знаний или ситуациях.

Примеры использования

Примеры использования математики в повседневной жизни:

СитуацияПример использования математики

Планирование бюджета	Использование математических расчетов для определения ежемесячных расходов и доходов.
Расчет времени	Использование математических операций при определении продолжительности событий и планировании расписания.
Изучение вероятности	Использование математических моделей для определения вероятности событий, например, при анализе рисков или прогнозировании результатов.
Дизайн и архитектура	Использование геометрии и пропорций для создания эстетически приятных и функциональных дизайнов и архитектурных решений.
Исследование данных	Использование статистических методов и анализа данных для извлечения полезной информации и принятия обоснованных решений.

Пример 1: «Когда в математике» в алгебре

В алгебре, когда речь идет о работе с алгебраическими выражениями, фраза «когда в математике» используется для обозначения условий, при которых выполняются определенные операции или свойства. Рассмотрим пример.

Пусть даны два алгебраических выражения: а и б. Когда в математике, в алгебре, мы говорим, что выражение а равно выражению б, мы подразумеваем, что они оба дают одинаковые числовые значения при любых значениях переменных, которые входят в эти выражения.

Например, если у нас есть выражение 2х + 3 и выражение 5 + х, то мы можем сказать, что они равны друг другу, когда х принимает значение 1. Это можно записать следующим образом: 2*1 + 3 = 5 + 1. То есть, «когда в математике, в алгебре, 2х + 3 равно 5 + х при х = 1».

Таким образом, использование фразы «когда в математике» в алгебре позволяет нам указать на определенные условия, при которых выполняются равенства или другие свойства алгебраических выражений.

Пример 2: «Когда в математике» в геометрии

В геометрии «когда в математике» используется для определения условий, при которых выполняются определенные свойства геометрических фигур.

Например, «когда в математике» в геометрии:

• Когда все стороны прямоугольника равны, то это становится квадратом.
• Когда все стороны треугольника равны, то это становится равносторонним треугольником.
• Когда две стороны треугольника равны, а угол между ними равен 90 градусов, то это становится прямоугольным треугольником.
• Когда все углы в многоугольнике равны, то это становится правильным многоугольником.

Использование «когда в математике» в геометрии помогает определить, какие условия должны быть выполнены для получения определенных свойств геометрических фигур и решения различных геометрических задач.

Вопрос-ответ:

Какие основные условия нужно знать в математике?

В математике есть несколько основных условий, которые нужно знать. Это, например, условие равенства, неравенства, условие эквивалентности, условие существования и условие единственности.

Какие примеры можно привести для основных условий в математике?

Примеры для основных условий в математике можно привести следующие: равенство: 2 + 2 = 4, неравенство: 3 > 2, эквивалентность: a + b = b + a, существование: в любом множестве чисел найдется наибольший элемент, единственность: единственный корень уравнения x^2 = 4 это x = 2 или x = -2.

Какие еще условия существуют в математике, кроме основных?

Помимо основных условий, в математике существуют еще такие условия, как условие возрастания или убывания функции, условие непрерывности функции, условие сходимости ряда и многие другие. В зависимости от конкретной области математики, могут быть и другие специфические условия.

Какие примеры можно привести для специфических условий в математике?

Примеры для специфических условий в математике зависят от конкретной области. Например, в анализе можно привести условие Дарбу, которое говорит о непрерывности функции в точке. В теории вероятностей можно привести условие независимости событий. В алгебре можно привести условие ассоциативности операции умножения. Примеров может быть множество, так как математика включает в себя много различных областей и теорий.

Пример 3: «Когда в математике» в тригонометрии

Когда в математике мы говорим о «когда», это может означать много разных вещей. В тригонометрии «когда» может относиться к определенному условию, которое должно быть выполнено, чтобы решить задачу или получить определенный результат.

В тригонометрии, одно из основных условий, связанных с «когда», — это условие прямоугольного треугольника. Если у нас есть прямоугольный треугольник, то мы можем использовать тригонометрические функции, такие как синус, косинус и тангенс, чтобы решить задачи, связанные с углами и сторонами треугольника.

Например, представим себе треугольник ABC, где угол А равен 30 градусам, сторона AB равна 5 и сторона BC равна 10. Мы можем использовать тригонометрическую функцию синуса, чтобы найти значение стороны АС, используя следующую формулу:

sin(A) = противолежащая сторона / гипотенуза

В нашем случае, sin(30) = AC / 10. Мы можем решить это уравнение, чтобы найти значение стороны АС. В данном случае, AC будет равно 5.

Таким образом, когда имеется прямоугольный треугольник и заданы значения некоторых сторон и углов, мы можем использовать тригонометрические функции, чтобы найти значения других сторон и углов.

В следующих примерах мы рассмотрим другие ситуации, где «когда» в тригонометрии может быть использовано для решения задач и получения результатов.

Видео по теме: