Что такое комментирование по математике
Содержимое
- 1 Что такое комментирование по математике
Комментирование по математике — это процесс объяснения и обсуждения математических концепций, задач и решений. Статья рассказывает о том, как комментирование помогает учиться математике, развивает логическое мышление и способствует глубокому пониманию темы. Здесь вы найдете полезные советы по комментированию математических задач и узнаете, какие преимущества оно может принести в обучении и повседневной жизни.
Математика — это одна из самых фундаментальных наук, которая исследует свойства чисел, пространства, форм и изменений. Комментирование по математике играет важную роль в объяснении и демонстрации математических концепций, теорем и решений задач. Это процесс написания комментариев, объясняющих шаги и логику решения математических задач и формулировок теорем.
Одной из основных целей комментирования по математике является помощь читателю в понимании математических концепций и методов. Комментарии могут содержать объяснения, примеры, аналогии и ссылки на другие математические источники. Они помогают читателю разобраться в сложных математических терминах и формулах, а также понять логику и последовательность шагов решения задачи.
Пример комментирования по математике:
Задача: Найдите сумму первых 10 членов арифметической прогрессии с первым членом 2 и разностью 3.
Решение: Для нахождения суммы первых n членов арифметической прогрессии можно использовать формулу: Sn = (n/2)(a + l), где Sn — сумма, n — количество членов, a — первый член, l — последний член.
В данном случае у нас задано n = 10, a = 2 и разность d = 3. Последний член l можно найти с помощью формулы l = a + (n — 1)d. Подставляем значения и получаем l = 2 + (10 — 1)3 = 2 + 27 = 29.
Теперь можем найти сумму: Sn = (10/2)(2 + 29) = 5 * 31 = 155.
Таким образом, сумма первых 10 членов арифметической прогрессии с первым членом 2 и разностью 3 равна 155.
Комментирование по математике
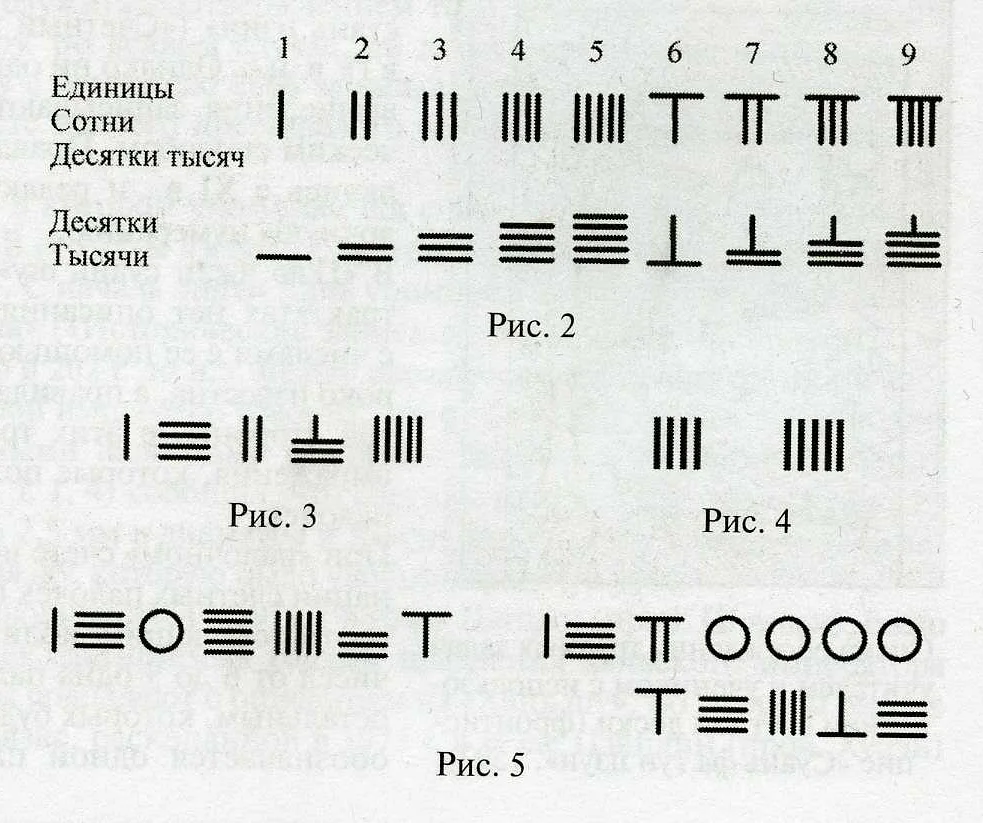
Основные принципы комментирования по математике включают:
- Ясность и точность: комментарии должны быть четкими и точно описывать математические операции и концепции.
- Последовательность: комментарии должны следовать в логической последовательности, чтобы читатель мог легко следовать за аргументацией.
- Краткость: комментарии должны быть краткими и конкретными, чтобы избежать ненужных деталей и повторений.
- Использование символов: комментарии могут содержать математические символы и обозначения, чтобы более точно передать смысл выражений.
Примеры комментирования по математике:
«Для решения данной задачи мы используем метод множителей Лагранжа, чтобы найти экстремум функции при ограничениях.»
«В этом шаге мы применяем теорему Пифагора для вычисления гипотенузы треугольника.»
Комментирование по математике является важным инструментом для обмена и передачи знаний в области математики. Оно помогает улучшить понимание математических концепций и методов, а также способствует более эффективному применению математики в различных областях науки и техники.
Суть комментирования

Основная цель комментирования — помочь читателю следовать и понять рассуждения автора. Комментарии должны быть ясными, лаконичными и информативными. Они должны содержать достаточно информации, чтобы читатель мог проверить правильность решения и, при необходимости, повторить его самостоятельно.
Комментирование может включать в себя описание используемых формул, определения терминов, объяснение применяемых методов и стратегий, а также обоснование выбора определенных шагов в решении. Комментарии также могут содержать дополнительные материалы, например, ссылки на дополнительные источники, где читатель может найти более подробную информацию.
Важно помнить, что комментирование должно быть понятным для широкой аудитории, включая тех, кто не имеет глубоких знаний в математике. Поэтому необходимо избегать излишне сложной терминологии и формул, особенно если они несущественны для общего понимания решения.
Хорошая практика комментирования — это использование нумерованных или маркированных списков, чтобы структурировать комментарии и сделать их более удобочитаемыми. Также рекомендуется использовать определенный стиль комментирования, чтобы сделать его последовательным и легко читаемым.
Примеры комментирования в математике:
- Объяснение шагов решения задачи: «Получаем необходимое уравнение, затем приводим его к каноническому виду»
- Обоснование выбора метода: «Используем метод математической индукции, так как он позволяет доказать утверждение для всех натуральных чисел»
- Описание формулы или термина: «Формула квадратного уравнения имеет вид: ax^2 + bx + c = 0, где a, b и c — коэффициенты»
В целом, комментирование в математике играет важную роль в обмене знаниями и обучении. Оно позволяет разделять и передавать математические идеи и методы, а также улучшает понимание и уверенность в решении математических задач.
Принципы комментирования
Комментирование кода в математике играет важную роль, поскольку помогает улучшить понимание работы программы, а также упростить сопровождение и отладку. Ниже приведены основные принципы комментирования, которые помогут сделать код более понятным и читаемым.
1. Описывайте назначение кода: Каждый комментарий должен пояснять, что делает определенная часть кода и какой результат она должна вернуть. Это поможет другим разработчикам, а также вам самим при возвращении к коду после некоторого времени.
2. Используйте понятные имена переменных: Давайте переменным и функциям понятные и описательные имена, чтобы комментирование кода было минимальным. Хорошие имена переменных сократят необходимость в дополнительных комментариях.
3. Поясняйте сложные участки кода: Если в коде есть сложные или нетривиальные участки, обязательно добавьте комментарии, поясняющие, как они работают или что они делают. Это поможет другим разработчикам понять вашу логику и избежать ошибок при изменении кода.
4. Избегайте лишних комментариев: Комментарии должны быть информативными и не должны повторять то, что уже ясно из самого кода. Избегайте комментирования каждой строчки кода, особенно если они не несут дополнительной информации.
5. Обновляйте комментарии при изменении кода: Если вы вносите изменения в код, не забудьте обновить соответствующие комментарии, чтобы они оставались актуальными. Устаревшие комментарии могут привести к неправильному пониманию кода и ошибкам в его использовании.
Следуя этим принципам комментирования, вы сможете создавать более читаемый и понятный код, который будет легче поддерживать и дорабатывать.
Примеры комментирования
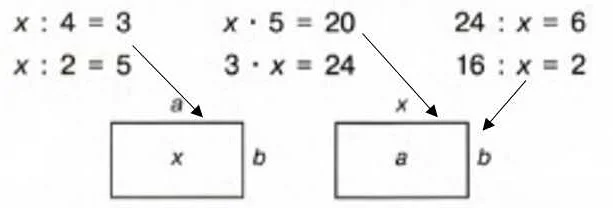
Приведем несколько примеров комментирования математических выражений:
ПримерКомментарий
| 2 + 2 | Сложение двух чисел |
| 5 * 8 | Умножение двух чисел |
| sqrt(16) | Извлечение квадратного корня из числа |
| x^2 + y^2 = r^2 | Уравнение окружности с центром в начале координат |
Комментарии помогают разобраться в смысле математических выражений и упрощают их понимание.
Комментирование в алгебре

Комментарии в алгебре могут быть использованы для:
- Пояснения шагов решения задачи: комментарии помогают разъяснить каждый шаг решения, объяснить выбор определенной операции или применение конкретного правила.
- Описания используемых формул и обозначений: комментарии позволяют пояснить значение и смысл использованных символов, формул и обозначений в задаче.
- Анализа ошибок: комментарии позволяют выделить и объяснить ошибку в решении задачи, помогая ученикам понять, где они допустили ошибку.
Пример использования комментариев в алгебре:
Задача: Решить уравнение 2x + 5 = 15.
Шаг 1: Вычитаем 5 из обеих частей уравнения, чтобы избавиться от слагаемого 5 на левой стороне:
2x + 5 — 5 = 15 — 5
Шаг 2: Упрощаем уравнение:
2x = 10
Шаг 3: Делим обе части уравнения на 2, чтобы найти значение переменной x:
2x / 2 = 10 / 2
x = 5
Таким образом, значение переменной x равно 5.
Комментирование в геометрии
Один из ключевых принципов комментирования в геометрии — это ясное и точное описание геометрических фигур. Комментарии должны быть понятными для читателя и содержать достаточно информации для полного понимания объекта или концепции.
В комментировании геометрии также важно использование ключевых слов и терминов, чтобы указать на особенности и свойства фигур. Формулы и уравнения могут быть использованы для более точного описания и объяснения геометрических понятий.
Пример комментирования в геометрии:
Треугольник ABC — прямоугольный треугольник со сторонами AB, BC и AC. Угол BAC равен 90 градусам. Сторона AB является гипотенузой треугольника. Согласно теореме Пифагора, квадрат длины гипотенузы равен сумме квадратов длин катетов. Таким образом, AC^2 + BC^2 = AB^2.»
Вывод: Комментирование в геометрии помогает читателям лучше понять и запомнить геометрические фигуры и связанные с ними концепции. Ясные и точные комментарии с использованием ключевых терминов и формул способствуют более глубокому пониманию и применению геометрии.
Комментирование в теории чисел
Одним из основных принципов комментирования в теории чисел является ясность и ясность изложения. Все комментарии должны быть написаны таким образом, чтобы их могли понять даже те, кто не является экспертом в данной области. Это особенно важно, учитывая сложность и абстрактность некоторых концепций в теории чисел.
Комментирование в теории чисел также может включать использование примеров и иллюстраций, чтобы проиллюстрировать и объяснить различные идеи и результаты. Примеры могут быть в виде числовых последовательностей, графиков или диаграмм, которые помогают визуализировать идеи и облегчить их понимание.
Важно помнить, что комментирование в теории чисел не только служит для объяснения математических концепций, но также может помочь в подтверждении или опровержении результатов и теорем, а также дать указания по дальнейшим исследованиям и развитию данной области.
Чтобы сделать комментирование более структурированным и читабельным, часто используются упорядоченные и неупорядоченные списки. В упорядоченном списке используется тег <ol>, а каждый элемент списка обозначается тегом <li>. В неупорядоченном списке используется тег <ul>, а каждый элемент списка также обозначается тегом <li>.
Примером комментирования в теории чисел может служить следующий упорядоченный список:
- Определение простого числа
- Свойства простых чисел
- Доказательство теоремы Ферма
- Применение чисел Фибоначчи в теории чисел
Такой список позволяет организовать комментарии в логическом порядке и помочь читателю лучше понять и усвоить информацию.
Комментирование в математическом анализе
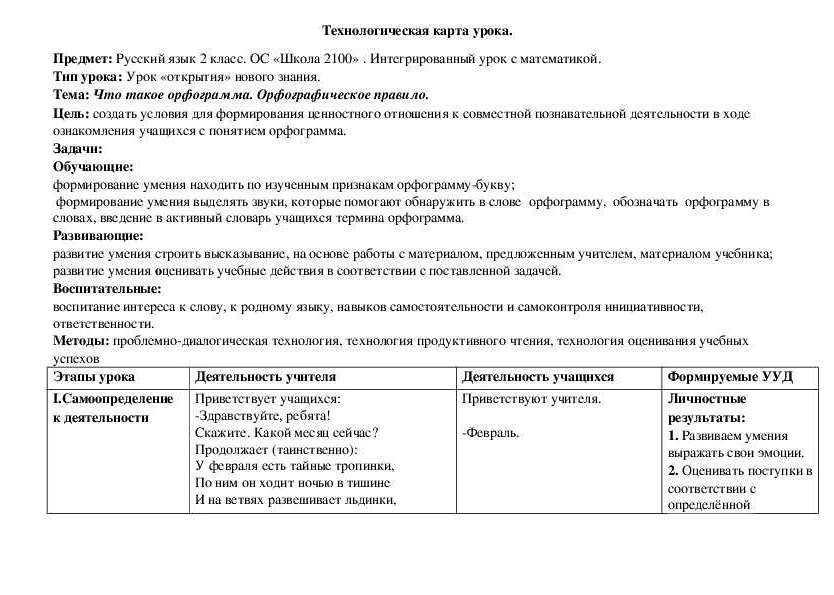
В комментариях к математическому анализу можно использовать различные подходы и техники. Одним из наиболее распространенных методов является разбиение решаемой задачи на отдельные шаги и пояснение каждого шага поочередно. Это позволяет детально описать процесс решения, упрощение и приведение математических выражений, а также использование различных теорем и методов анализа.
Другим полезным подходом является приведение примеров и иллюстраций. Показывая конкретные числовые примеры и графики, можно помочь читателю или слушателю лучше понять абстрактные математические понятия. Например, в комментариях к дифференциальному исчислению можно привести примеры вычислений производных, графиков функций и применения полученных результатов в реальной жизни.
Комментирование в математическом анализе также позволяет подчеркнуть ключевые моменты и особенности рассматриваемых понятий. Например, можно дополнительно описать важность точности и ограничений при использовании численных методов, а также указать на связь с другими разделами математики или применение в других науках.
В итоге, комментирование в математическом анализе является важным элементом образовательного процесса. Оно способствует лучшему пониманию математических концепций, помогает применить полученные знания к практическим задачам и развивает навыки логического мышления и анализа.
Видео по теме:
Что такое комментирование по математике?
Комментирование по математике — это процесс добавления пояснений и объяснений к математическим выражениям, формулам или решениям. Это помогает уточнить и разъяснить математическую логику и шаги решения проблемы.
Зачем нужно комментировать математические выражения?
Комментирование математических выражений полезно для облегчения понимания и чтения математических решений. Оно помогает другим людям, а также самому автору лучше понять логику решения и обосновать свои действия. Комментарии также помогают избежать ошибок и обнаружить логические проблемы в решении.
Какие принципы следует соблюдать при комментировании по математике?
При комментировании по математике следует придерживаться нескольких принципов. Во-первых, комментарии должны быть ясными и информативными, чтобы другие люди могли легко понять мысли автора. Во-вторых, комментарии должны быть точными и не оставлять места для неоднозначностей. В-третьих, комментарии должны быть логически связаны с соответствующими математическими выражениями и не должны противоречить им.
Как можно комментировать по математике?
Существует несколько способов комментирования по математике. Один из них — использование комментариев в коде программы или в LaTeX-файлах. Другой способ — добавление комментариев в текстовый документ, где автор может пояснить свои шаги решения или объяснить математические термины и определения. Также можно использовать комментарии в учебных пособиях, чтобы помочь студентам понять математические понятия и концепции.
Можете привести примеры комментирования по математике?
Конечно! Вот пример комментирования решения уравнения: «Для решения этого уравнения мы сначала привели его к виду, где все переменные находятся слева от знака равенства. Затем мы применили метод последовательных приближений, чтобы найти приближенное решение. На следующем шаге мы проверили, что найденное приближение действительно является решением исходного уравнения. В итоге получилось решение x = 3.5». В этом примере комментарии помогают понять, как автор пришел к решению и какие шаги были предприняты.
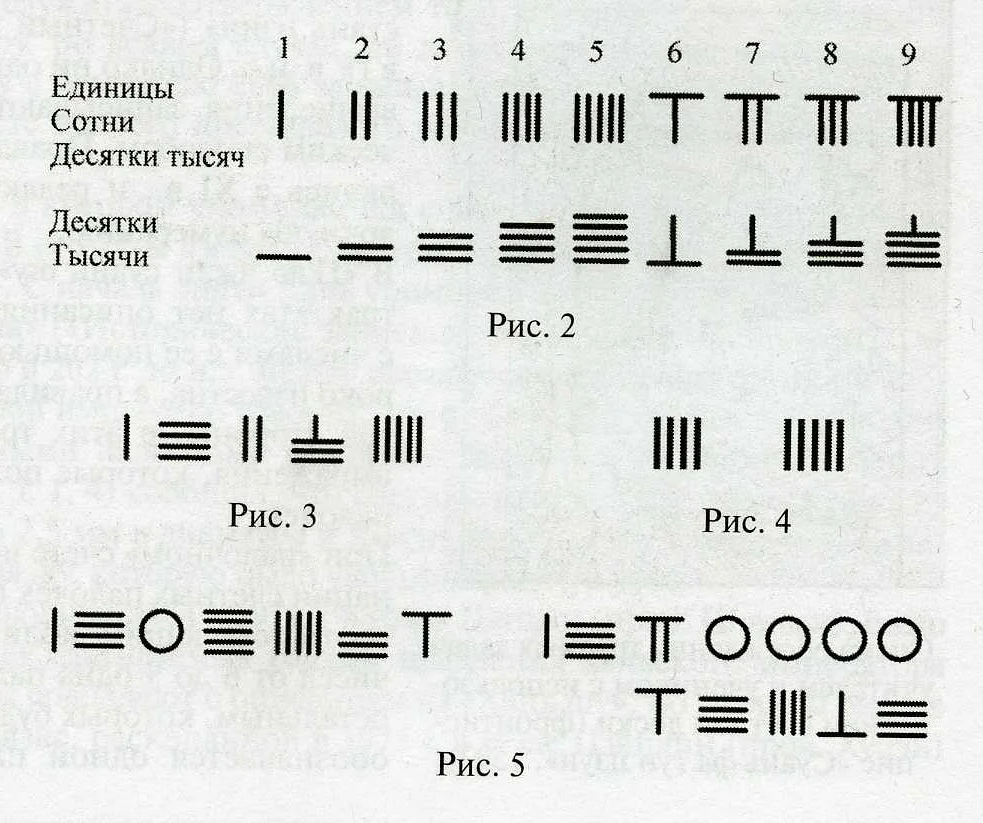




Статья очень интересная и полезная! Я всегда думала, что математика — это скучно и сложно, но благодаря этому материалу я поняла, что комментирование по математике может быть увлекательным и понятным. Принципы комментирования, которые описаны в статье, помогают увидеть связи и закономерности в математических задачах. И примеры, которые приведены, иллюстрируют, как правильно анализировать и объяснять решение задач. Теперь я понимаю, что комментирование помогает не только углубить свои знания в математике, но и развить логическое мышление. Большое спасибо автору за такую полезную статью!