Что такое математическая грамотность 8 класс

Математическая грамотность в 8 классе — это способность ученика применять математические знания и навыки для решения сложных задач, анализа и интерпретации данных. Важно развивать учеников в этой области, чтобы они могли успешно справляться с математическими трудностями и применять свои знания в повседневной жизни.

Математическая грамотность является одним из важнейших навыков, которые ученик должен освоить в 8 классе. Она включает в себя понимание и умение применять основные математические понятия и методы решения задач. Владение математической грамотностью позволяет развивать логическое мышление, аналитические навыки и способствует успешной учебе в других предметах.

Основные понятия, которые необходимо понять и усвоить в 8 классе, включают различные области математики, такие как алгебра, геометрия, вероятность и статистика. Ученик должен знать основные математические операции и их свойства, уметь работать с уравнениями и неравенствами, понимать основные геометрические фигуры и их свойства, а также уметь анализировать статистические данные и решать задачи на вероятность.

Примеры задач на математическую грамотность в 8 классе могут быть разнообразными. Например, задачи на нахождение корней квадратного уравнения, решение систем уравнений, построение графиков функций, нахождение площади и периметра геометрических фигур, анализ статистических данных и решение задач на вероятность. Решение таких задач требует не только знания математических понятий, но и умения применять их для решения практических задач.

Математическая грамотность является основой математического образования и является важным элементом подготовки учеников к дальнейшему обучению и решению жизненных задач. Развитие математической грамотности в 8 классе требует усилий и постоянной практики, но оно является неотъемлемой частью учебного процесса и помогает развивать у учеников не только математические навыки, но и аналитическое мышление и способность к решению сложных задач.

Математическая грамотность 8-го класса:

Основные понятия, которые важно освоить в 8-м классе, включают в себя:

• Пропорциональность: учащиеся должны понимать, как определять пропорциональность между величинами и решать задачи на ее основе.
• Проценты: ученикам необходимо овладеть навыками работы с процентами, включая расчеты процентных значений, изменение процентов и прочие операции.
• Алгебраические выражения: ученики должны научиться работать с алгебраическими выражениями, включая их упрощение, факторизацию и решение уравнений и неравенств.
• Геометрия: учащиеся должны освоить основные геометрические понятия, такие как углы, треугольники, прямоугольники, окружности и т.д., а также научиться применять геометрические методы для решения задач.
• Статистика и вероятность: ученикам необходимо овладеть навыками работы с таблицами, графиками, расчетами средних значений и решением задач на вероятность.

Освоение этих основных понятий позволит ученикам успешно продолжить обучение математике в старших классах и применять их знания в реальной жизни.

Основные понятия и определения

Число — это абстрактное понятие, используемое для измерения и подсчета количества или величины чего-либо.

Целое число — число, которое не имеет дробной части и может быть положительным, отрицательным или нулем.

Рациональное число — число, которое может быть представлено в виде дроби, где числитель и знаменатель являются целыми числами.

Натуральное число — положительное целое число, которое используется для подсчета и упорядочивания объектов в множестве.

Десятичная дробь — число, записанное в десятичной системе счисления, где десятичная точка разделяет целую часть числа от дробной части.

Процент — это часть от целого, выраженная в сотых долях. Проценты часто используются для выражения отношений или изменений величин.

Уравнение — математическое предложение, в котором две части (левая и правая) связаны знаком равенства.

Решение уравнения — это значение или набор значений переменных, которые делают уравнение истинным.

График — это визуальное представление данных или математической функции на декартовой плоскости. Графики могут использоваться для анализа и визуализации зависимостей между переменными.

Функция — это математическое правило, которое связывает каждый элемент из одного множества с одним или несколькими элементами из другого множества.

Последовательность — это упорядоченный набор чисел или объектов, которые следуют друг за другом в определенном порядке.

Вероятность — это числовая характеристика, которая измеряет степень возможности наступления события.

Статистика — это наука, которая изучает сбор, анализ, интерпретацию и представление данных. Статистика используется для описания и обобщения информации о различных явлениях и явлениях.

Примеры задач на алгебру

Задача 1:

Найдите значение выражения 5x + 2y при x = 3 и y = 4.

Решение:

Подставляем значения переменных:

5 * 3 + 2 * 4 = 15 + 8 = 23.

Ответ: 23.

Задача 2:

Решите уравнение 2x — 7 = 15.

Решение:

Добавляем 7 к обеим частям уравнения:

2x = 15 + 7 = 22.

Делим обе части на 2:

x = 22 / 2 = 11.

Ответ: x = 11.

Задача 3:

Упростите выражение (x + 3)(x — 2).

Решение:

Умножаем каждый член первого скобочного выражения на каждый член второго скобочного выражения:

x * x + x * (-2) + 3 * x — 2 * 3 = x^2 — 2x + 3x — 6.

Сокращаем подобные слагаемые:

x^2 + x — 6.

Ответ: x^2 + x — 6.

Простейшие геометрические фигуры

К наиболее простым геометрическим фигурам относятся точка, прямая, отрезок и угол.

Точка — это элементарное понятие геометрии, которое не имеет ни размеров, ни формы. Она обозначается заглавной буквой латинского алфавита. Например, точка A.

Прямая — это геометрическая фигура, которая не имеет ни ширины, ни толщины, но имеет бесконечную длину. Она обозначается строчной буквой латинского алфавита или двумя заглавными буквами. Например, прямая a или прямая AB.

Отрезок — это часть прямой, которая имеет начало и конец. Он обозначается двумя заглавными буквами, между которыми ставится символ «−». Например, отрезок AB или AB−.

Угол — это область плоскости, ограниченная двумя полупрямыми с общим началом. Он обозначается тремя заглавными буквами или символом ∠. Например, угол BAC или ∠BAC.

Простейшие геометрические фигуры являются основой для изучения более сложных фигур, таких как треугольник, квадрат, прямоугольник и многоугольники. Понимание и умение работать с этими базовыми фигурами являются основой математической грамотности в 8 классе и позволяют решать разнообразные задачи в геометрии.

Примеры задач на геометрию

1. Найти площадь прямоугольника, если его стороны равны 6 см и 9 см.

2. Найти площадь круга, если его радиус равен 5 см.

3. Найти длину окружности, если ее радиус равен 8 см.

4. Найти площадь треугольника, если его высота равна 10 см, а основание равно 6 см.

5. Найти площадь параллелограмма, если его основание равно 8 см, а высота равна 5 см.

6. Найти площадь трапеции, если ее основания равны 7 см и 9 см, а высота равна 4 см.

7. Найти объем куба, если длина его ребра равна 4 см.

8. Найти объем цилиндра, если его радиус основания равен 3 см, а высота равна 10 см.

9. Найти объем конуса, если его радиус основания равен 5 см, а высота равна 8 см.

10. Найти объем шара, если его радиус равен 6 см.

11. Найти площадь поверхности куба, если длина его ребра равна 3 см.

12. Найти площадь поверхности цилиндра, если его радиус основания равен 2 см, а высота равна 6 см.

13. Найти площадь поверхности конуса, если его радиус основания равен 4 см, а образующая равна 10 см.

14. Найти площадь поверхности шара, если его радиус равен 7 см.

Системы уравнений и неравенств

Системы уравнений состоят из нескольких уравнений с неизвестными, которые нужно найти. Решение системы уравнений – это такой набор значений переменных, при котором все уравнения системы выполняются одновременно. Система уравнений может иметь одно или несколько решений, а также быть несовместной, то есть не иметь решений.

Системы неравенств также состоят из нескольких неравенств с неизвестными. Решение системы неравенств – это такой набор значений переменных, при котором все неравенства системы выполняются одновременно. При решении системы неравенств возможны различные варианты решений, включая интервалы и неравенства с объединением и пересечением.

Решение систем уравнений и неравенств может быть найдено различными методами, включая подстановку, метод Гаусса и графический метод. Для более сложных систем может потребоваться использование матриц и алгоритмов решения.

Системы уравнений и неравенств имеют широкий спектр применения в реальной жизни. Они используются для моделирования и решения задач из различных областей, включая физику, экономику, инженерию и другие.

Важно уметь правильно формулировать системы уравнений и неравенств, а также уметь решать их с помощью применения соответствующих методов. Это позволяет анализировать и решать сложные задачи и применять математические знания на практике.

Примеры задач на системы уравнений и неравенств

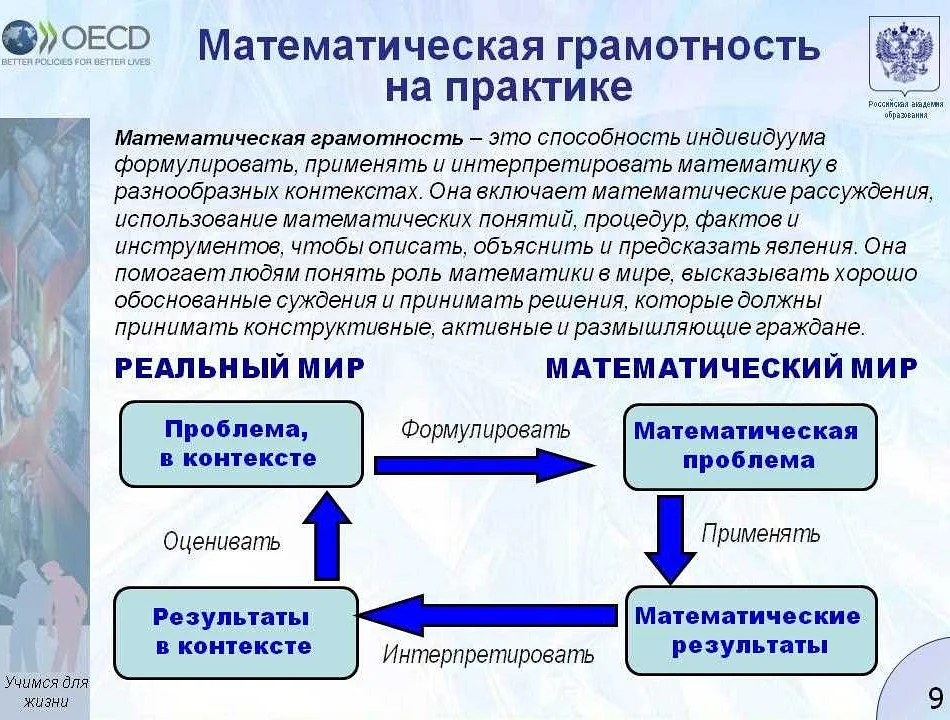
Пример 1:

Решите систему уравнений:

x + y = 5

2x — y = 1

Решение:

Способ 1: Метод подстановки.

Исходная система уравнений:

x + y = 5

2x — y = 1

Из первого уравнения находим x = 5 — y.

Подставляем это значение во второе уравнение:

2(5 — y) — y = 1

Раскрываем скобки:

10 — 2y — y = 1

Складываем слагаемые:

10 — 3y = 1

Вычитаем 10 из обеих частей уравнения:

-3y = -9

Разделим обе части уравнения на -3:

y = 3

Подставим найденное значение y в первое уравнение:

x + 3 = 5

Вычитаем 3 из обеих частей уравнения:

x = 2

Ответ: x = 2, y = 3.

Способ 2: Метод сложения.

Исходная система уравнений:

x + y = 5

2x — y = 1

Умножим первое уравнение на 2:

2(x + y) = 2 * 5

Раскрываем скобки:

2x + 2y = 10

Сложим это уравнение с вторым уравнением:

2x + 2y + (2x — y) = 10 + 1

Складываем слагаемые:

4x + y = 11

Решаем полученное уравнение:

4x + y = 11

2x — y = 1

Сложим эти два уравнения:

4x + y + (2x — y) = 11 + 1

Складываем слагаемые:

6x = 12

Разделим обе части уравнения на 6:

x = 2

Подставим найденное значение x в первое уравнение:

2 + y = 5

Вычитаем 2 из обеих частей уравнения:

y = 3

Ответ: x = 2, y = 3.

Пример 2:

Решите систему неравенств:

2x — 3y ≥ 4

x + y < 5

Решение:

Исходная система неравенств:

2x — 3y ≥ 4

x + y < 5

Из второго неравенства находим y < 5 — x.

Подставляем это значение в первое неравенство:

2x — 3(5 — x) ≥ 4

Раскрываем скобки:

2x — 15 + 3x ≥ 4

Складываем слагаемые:

5x — 15 ≥ 4

Добавляем 15 к обеим частям неравенства:

5x ≥ 4 + 15

Складываем числа:

5x ≥ 19

Делим обе части неравенства на 5:

x ≥ 3.8

Подставим найденное значение x во второе неравенство:

3.8 + y < 5

Вычитаем 3.8 из обеих частей неравенства:

y < 5 — 3.8

y < 1.2

Ответ: x ≥ 3.8, y < 1.2.

Статистика и вероятность

Статистика изучает сбор, анализ и интерпретацию данных. Она основана на сборе данных и их представлении в виде таблиц, графиков и диаграмм. Статистика позволяет исследовать различные характеристики данных, такие как среднее значение, медиана, дисперсия и стандартное отклонение. Она также позволяет делать выводы на основе результатов анализа данных и проверять гипотезы.

Вероятность изучает случайные события и их вероятность. Она позволяет рассчитывать вероятность возникновения определенного события на основе известных данных. Вероятность может быть представлена числом от 0 до 1, где 0 означает невозможность события, а 1 — его абсолютное достоверность. Вероятность может быть рассчитана с использованием различных методов, таких как классическая вероятность, частотная вероятность и условная вероятность.

Статистика и вероятность имеют множество применений в реальной жизни. Они используются для анализа данных в научных исследованиях, бизнесе, финансах, медицине, социологии и других областях. Знание основных понятий и методов статистики и вероятности позволяет принимать обоснованные решения на основе анализа данных и предсказывать вероятные результаты.

Примеры задач на статистику и вероятность

Пример 1:

В классе 8А учатся 30 человек. Разделение по полу следующее: 16 мальчиков и 14 девочек. Какова вероятность выбрать случайного ученика этого класса и получить девочку?

Решение:

Общее количество учеников в классе: 30. Количество девочек: 14. Вероятность выбрать девочку равна отношению количества девочек к общему количеству учеников: 14/30 = 7/15.

Ответ: Вероятность выбрать случайного ученика этого класса и получить девочку равна 7/15.

Пример 2:

Вероятность того, что студент Саша сдаст экзамен по математике, равна 0.8. Вероятность того, что студент Миша сдаст экзамен, равна 0.6. Какова вероятность того, что оба студента сдадут экзамены по математике?

Решение:

Вероятность того, что оба студента сдадут экзамены, равна произведению вероятностей их успеха: 0.8 * 0.6 = 0.48.

Ответ: Вероятность того, что оба студента сдадут экзамены по математике, равна 0.48.

Пример 3:

В группе из 50 студентов 30 из них учатся на факультете математики, а остальные 20 — на факультете физики. Вероятность того, что случайно выбранный студент учится на факультете математики, равна…

Решение:

Общее количество студентов в группе: 50. Количество студентов на факультете математики: 30. Вероятность выбрать студента с факультета математики равна отношению количества студентов на факультете математики к общему количеству студентов: 30/50 = 3/5.

Ответ: Вероятность того, что случайно выбранный студент учится на факультете математики, равна 3/5.

Вопрос-ответ:

Какие основные понятия и примеры задач изучаются на уроках математики в 8 классе?

В 8 классе ученики изучают такие основные понятия, как квадратные уравнения и системы уравнений, показательные функции и их свойства, а также пропорциональные и функциональные зависимости. Примеры задач могут быть разнообразными, например, решение квадратного уравнения, определение области определения функции, решение системы уравнений методом подстановки и т. д.

Как можно применить знания математики в реальной жизни, основанные на математической грамотности 8 класса?

Знания математики, полученные в 8 классе, могут быть применимы во многих сферах жизни. Например, при планировании бюджета и расчете расходов, при решении задач по геометрии для постройки или измерения объектов, при работе с процентами и процентными расчетами, а также при анализе данных и построении графиков.

Какие методы решения квадратных уравнений изучаются в 8 классе?

В 8 классе ученики изучают методы решения квадратных уравнений, такие как метод выделения квадратного корня, метод приведения к каноническому виду, метод дискриминанта и метод графического решения. Каждый из этих методов позволяет решить квадратное уравнение и найти все его корни.

Какие свойства показательных функций изучаются в 8 классе?

В 8 классе ученики изучают такие свойства показательных функций, как свойства степени с натуральным показателем, свойства степени с рациональным показателем, свойства умножения и деления показательных функций, свойства возведения в отрицательную степень и свойства корня из показательной функции.

Какие задачи могут быть связаны с пропорциональными и функциональными зависимостями, изучаемыми в 8 классе?

Задачи, связанные с пропорциональными и функциональными зависимостями, могут быть различными. Например, задачи на нахождение пропорциональности величин, задачи на нахождение коэффициента пропорциональности, задачи на построение графиков функций, задачи на нахождение значения функции при заданном значении аргумента и т. д.

Что такое математическая грамотность?

Математическая грамотность — это способность человека применять математические знания и навыки для решения различных задач и ситуаций в жизни. Это включает в себя понимание основных математических понятий, умение проводить логические рассуждения, анализировать информацию и применять математические методы в практических ситуациях.

Видео по теме: