Математические модели роста злокачественных опухолей что такое

Математические модели роста злокачественных опухолей – это методы, основанные на математических уравнениях, которые позволяют моделировать и предсказывать развитие опухолей. Эти модели помогают понять процессы, протекающие в организме при онкологических заболеваниях и могут быть использованы для разработки новых методов лечения и диагностики опухолей.

Злокачественные опухоли являются одной из самых серьезных проблем современной медицины. Они возникают, когда клетки организма начинают не контролируемо делиться и формировать опухоль. Чтобы более полно понять процесс развития и роста опухолей, ученые разрабатывают математические модели, которые помогают предсказать их поведение и эволюцию.

Математические модели роста злокачественных опухолей основываются на принципах и законах, которые управляют процессами в организме. Они учитывают множество факторов, таких как скорость деления клеток, миграция клеток, апоптоз (программированная гибель клеток), а также взаимодействие опухоли с иммунной системой и кровеносной системой.

Математические модели позволяют предсказать, как опухоль будет расти и распространяться в организме, что является важным фактором для определения стратегии лечения. Они помогают врачам принимать решения о выборе методов лечения и оптимальном времени для проведения операций или начала химиотерапии. Также модели позволяют оценить эффективность различных методов лечения и проводить виртуальные эксперименты для определения оптимальной дозировки препаратов.

Одним из важных достижений математических моделей роста злокачественных опухолей является возможность прогнозировать вероятность рецидива опухоли после проведения лечения. Это позволяет врачам принимать решения о необходимости дополнительных мероприятий, таких как радиотерапия или гормональная терапия, для предотвращения рецидива.

Таким образом, математические модели роста злокачественных опухолей являются мощным инструментом в борьбе с раковыми заболеваниями. Они позволяют более точно предсказывать развитие и поведение опухолей, что способствует более эффективному лечению и улучшению выживаемости пациентов.

Математические модели злокачественных опухолей: что это?

Эти модели строятся на основе наблюдений и экспериментальных данных о поведении опухолей и их взаимодействии с окружающими тканями. Они помогают исследователям лучше понять процессы, происходящие в теле при развитии опухолей, и предсказать их дальнейшее поведение.

Математические модели злокачественных опухолей основаны на принципах математического моделирования, которые позволяют описать различные факторы, влияющие на рост опухоли, такие как скорость деления клеток, их миграция и взаимодействие с другими клетками и тканями.

Использование таких моделей позволяет исследователям проводить виртуальные эксперименты, моделировать различные сценарии развития опухоли и оценивать эффективность различных методов лечения. Это помогает в разработке новых стратегий борьбы с раком и повышении эффективности существующих методов лечения.

Математические модели злокачественных опухолей играют важную роль в онкологии и являются мощным инструментом для исследования и прогнозирования развития раковых заболеваний.

Видео по теме:

Определение и основные характеристики

Основная цель таких моделей — предсказывать, как будет развиваться опухоль в будущем и как она будет влиять на организм. Они могут помочь врачам и исследователям принять более информированные решения о лечении и предотвращении рака.

Математические модели роста опухолей основаны на ряде основных характеристик, которые описывают процесс развития рака:

• Скорость роста: это скорость, с которой опухоль увеличивается в размере. Она может быть постоянной или изменяться со временем.
• Объем опухоли: это объем, занимаемый опухолью в организме. Он может быть измерен в миллиметрах кубических или других единицах объема.
• Границы опухоли: это границы, отделяющие опухоль от здоровых тканей. Они могут быть более или менее четкими, что указывает на степень инвазии опухоли.
• Метастазы: это распространение раковых клеток из опухоли в другие части организма. Метастазы могут происходить через кровь или лимфу.

Математические модели роста злокачественных опухолей помогают исследователям и врачам лучше понять и предсказать развитие рака. Они также могут быть использованы для определения оптимального времени и метода лечения, а также для разработки новых методов диагностики и профилактики рака.

Принципы работы математических моделей

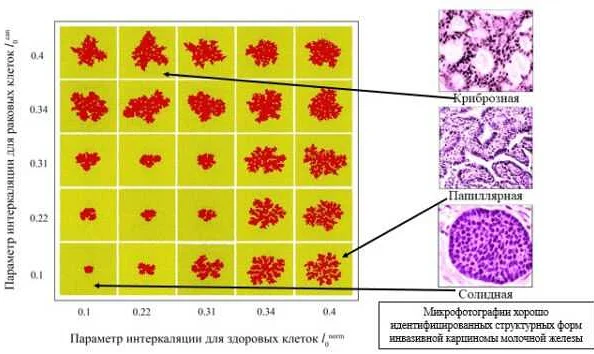
Принцип работы математических моделей заключается в том, что они учитывают различные факторы, влияющие на рост опухоли, и взаимодействие между ними. Например, модель может учитывать концентрацию питательных веществ, кровоснабжение опухоли, а также иммунную реакцию организма.

Модели также учитывают гетерогенность опухоли, то есть различия в ее составе, структуре и поведении. Это позволяет учесть различные типы опухолей и их вариации внутри организма.

Одним из основных принципов работы математических моделей является их адаптивность. Они могут быть изменены и уточнены на основе новых данных или откорректированы в соответствии с изменениями в пациенте. Это делает модели гибкими и способными адаптироваться к конкретным случаям.

Математические модели роста злокачественных опухолей имеют широкий спектр применений. Они могут быть использованы для прогнозирования эффективности лекарственных препаратов, оптимизации лечебного плана и оценки рисков. Они также могут служить инструментом для исследования механизмов развития опухоли и поиска новых подходов к лечению.

Вопрос-ответ:

Какие математические модели используются для описания роста злокачественных опухолей?

Существует несколько математических моделей, которые используются для описания роста злокачественных опухолей. Одна из самых распространенных моделей — это модель Гомпертца, которая основана на экспоненциальном росте опухоли. Также часто используются модели, основанные на системах дифференциальных уравнений, которые учитывают различные факторы, влияющие на рост опухоли, такие как приток и отток клеток, питание опухоли и т.д.

Какие данные используются для построения математических моделей роста опухолей?

Для построения математических моделей роста опухолей используются различные данные, включая данные о размерах опухоли, скорости роста, притоке и оттоке клеток, питании опухоли и другие параметры. Эти данные могут быть получены из клинических исследований, экспериментов на животных или моделирования на компьютере.

Как математические модели роста опухолей помогают в борьбе с раком?

Математические модели роста опухолей играют важную роль в борьбе с раком. Они позволяют ученым и врачам лучше понимать процессы, происходящие внутри опухоли, и предсказывать ее дальнейшее развитие. Это позволяет оптимизировать лечение и выбрать наиболее эффективные стратегии борьбы с раком, включая хирургическое вмешательство, лучевую и химиотерапию.

Какие особенности у математических моделей роста злокачественных опухолей?

Математические модели роста злокачественных опухолей обладают несколькими особенностями. Во-первых, они могут учитывать различные факторы, влияющие на рост опухоли, такие как приток и отток клеток, питание опухоли и другие параметры. Во-вторых, они могут предсказывать дальнейшее развитие опухоли и эффективность различных методов лечения. В-третьих, они могут быть использованы для оптимизации лечения и выбора наиболее эффективных стратегий борьбы с раком.

Как математические модели роста опухолей могут помочь в изучении рака?

Математические модели роста злокачественных опухолей позволяют ученым изучать и предсказывать динамику развития рака. Они помогают понять, как опухоль растет, распространяется и взаимодействует с окружающими тканями. Это позволяет разрабатывать новые методы диагностики и лечения рака, а также оптимизировать существующие терапевтические подходы.

Какие данные используются при создании математических моделей роста опухолей?

При создании математических моделей роста опухолей используются различные данные, такие как скорость роста опухоли, размеры и форма опухоли, а также среда, в которой она развивается. Эти данные собираются с помощью различных методов, включая клинические исследования, образовательные базы данных и эксперименты на животных и в лабораторных условиях. Используя эти данные, ученые создают математические модели, которые позволяют понять и предсказать поведение опухоли.

Какие преимущества имеют математические модели роста опухолей по сравнению с традиционными методами исследования рака?

Математические модели роста опухолей имеют несколько преимуществ по сравнению с традиционными методами исследования рака. Во-первых, они позволяют ученым изучать и предсказывать динамику развития опухоли в условиях, близких к реальным. Во-вторых, они помогают оптимизировать диагностику и лечение рака, позволяя разрабатывать индивидуальные подходы к каждому пациенту. В-третьих, математические модели позволяют проводить виртуальные эксперименты, что сокращает необходимость в экспериментах на животных или пациентах. В-четвертых, они помогают сократить затраты на исследования и ускорить процесс разработки новых методов диагностики и лечения рака.

Математические модели в исследованиях

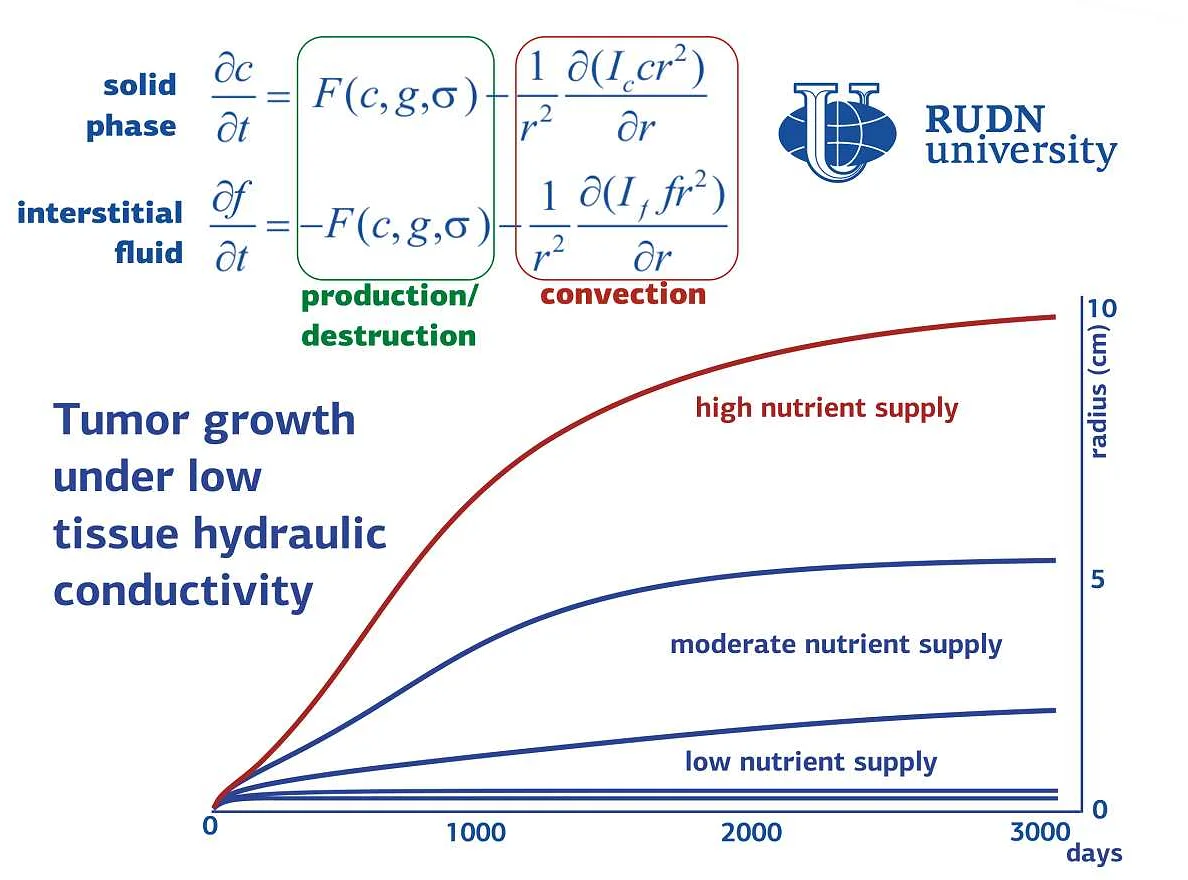
Математические модели роста злокачественных опухолей играют важную роль в научных исследованиях. Они позволяют ученым исследовать и предсказывать динамику развития опухоли, а также оценивать эффективность различных методов лечения.

Математические модели основываются на представлении опухоли как совокупности клеток, которые пролиферируют и мигрируют, образуя новые опухолевые участки. Модели учитывают различные факторы, влияющие на рост опухоли, такие как питание, кровоснабжение, иммунная система и действие лекарственных препаратов.

Существует несколько типов математических моделей, используемых в исследованиях злокачественных опухолей. Один из наиболее распространенных типов моделей — модель Гомпертца. Она основана на экспоненциальном законе роста опухоли и предсказывает, что скорость роста опухоли увеличивается со временем. Другие модели, такие как модель Гомпертца-Ричардса и модель Gompertz-Makeham, учитывают дополнительные факторы, такие как естественная смертность клеток и возраст пациента.

Математические модели роста злокачественных опухолей могут быть использованы для определения оптимального времени начала лечения, оценки прогноза и разработки новых методов лечения. Они могут помочь ученым и медицинским специалистам принимать обоснованные решения и улучшать результаты лечения пациентов.

Типы математических моделей роста опухолей

Математические модели роста злокачественных опухолей используются для изучения и прогнозирования их развития. Существует несколько основных типов таких моделей:

1. Экспоненциальная модель: основана на предположении, что опухоль растет с постоянной скоростью и непрерывно увеличивает свой размер со временем. Эта модель проста в использовании, но не всегда точно отражает реальные процессы роста опухолей.
2. Логистическая модель: учитывает ограничения роста опухоли, такие как наличие ограниченного пространства или ресурсов. Она предполагает, что в начальной стадии роста опухоль развивается экспоненциально, но затем ее рост замедляется, приближаясь к некоторому предельному значению.
3. Феноменологическая модель: основана на эмпирических наблюдениях и опирается на статистические данные о росте опухоли. Она может быть менее точной, но может быть полезной для описания общих тенденций и прогнозирования роста.
4. Модель клеточного автомата: использует сеточную структуру для моделирования роста опухоли. Каждая клетка на сетке представляет определенную область опухоли, и модель определяет правила для перемещения и деления клеток, что позволяет предсказывать и анализировать развитие опухоли.

Выбор конкретной модели зависит от целей и задач исследования, а также от доступных данных и предположений о процессах роста опухоли.

Основные преимущества математических моделей

• Предсказание и прогнозирование: Математические модели позволяют составить прогнозы о будущем развитии опухоли на основе имеющихся данных. Это помогает определить вероятность распространения рака, его скорость роста и возможные последствия.
• Оптимизация лечения: Модели позволяют оценить эффективность различных методов лечения и выбрать оптимальную стратегию. Они могут быть использованы для симуляции различных сценариев и проведения виртуальных экспериментов.
• Индивидуальный подход: Математические модели позволяют учитывать индивидуальные особенности пациента, такие как возраст, пол, образ жизни, генетические характеристики и другие факторы. Это позволяет более точно предсказывать и прогнозировать развитие опухоли у конкретного пациента.
• Экономическая эффективность: Математические модели позволяют оценить экономическую эффективность различных методов лечения и оптимизировать затраты на онкологическую помощь. Они помогают выявить наиболее эффективные и экономически целесообразные стратегии.
• Планирование и принятие решений: Математические модели позволяют проводить сценарный анализ и прогнозировать потенциальные последствия различных решений. Они помогают определить оптимальные стратегии в лечении и контроле злокачественных опухолей.

Все эти преимущества делают математические модели незаменимыми инструментами для исследования и борьбы с раком. Они позволяют сократить затраты на лечение, улучшить прогнозы выживаемости пациентов и повысить эффективность онкологической помощи в целом.

Как работают математические модели

Математические модели роста злокачественных опухолей основаны на принципе моделирования биологических процессов с использованием математических уравнений. Они позволяют исследовать и предсказывать развитие опухоли в организме человека.

Математическая модель опухоли представляет собой систему дифференциальных или разностных уравнений, которые описывают изменение размера опухоли со временем. В модели учитываются такие факторы, как скорость роста клеток, скорость делимости клеток и смертность клеток опухоли.

Модели роста опухолей основаны на предположении, что клетки опухоли размножаются и умирают с определенной скоростью. Эти скорости зависят от различных факторов, таких как питание, кислородное обеспечение, наличие кровеносных сосудов и иммунной системы. Математические модели позволяют учитывать эти факторы и предсказывать динамику роста опухоли.

Одним из основных применений математических моделей является определение оптимального лечения опухоли. Модели позволяют исследовать, как изменение параметров лечения, таких как дозировка препарата или время применения, может влиять на рост опухоли. Это позволяет оптимизировать лечение и повысить его эффективность.

Математические модели роста злокачественных опухолей являются мощным инструментом исследования и прогнозирования развития раковых заболеваний. Они позволяют ученым и врачам лучше понять процессы, происходящие в организме, и разработать более эффективные методы диагностики и лечения рака.

Применение математических моделей в медицине

Математические модели играют важную роль в области медицины, позволяя ученым и врачам более точно понять и предсказать различные процессы, связанные с заболеваниями и лечением. Они помогают в изучении разных аспектов болезней и оптимизации терапии, а также могут применяться для прогнозирования результатов и разработки новых методов лечения.

Одним из примеров применения математических моделей в медицине является изучение роста злокачественных опухолей. Модели роста опухолей позволяют ученым анализировать и предсказывать динамику развития опухолей, а также оценивать эффективность различных методов лечения. Это особенно полезно при планировании хирургических вмешательств и выборе оптимальной стратегии лечения опухолей.

Математические модели роста опухолей основаны на компьютерных алгоритмах и статистических методах, которые учитывают различные параметры, такие как размер опухоли, скорость роста, инвазивность и другие факторы. Эти модели могут быть использованы для проведения виртуальных экспериментов и оптимизации лечебного процесса, что помогает улучшить результаты терапии и уменьшить риск осложнений.

Кроме того, математические модели применяются для изучения других заболеваний, таких как сердечно-сосудистые заболевания, рак, инфекционные болезни и др. Они помогают ученым и врачам более глубоко понять механизмы развития болезней, выявить факторы риска и разработать эффективные стратегии профилактики и лечения.

В заключение, применение математических моделей в медицине играет важную роль в понимании и лечении различных заболеваний. Они позволяют ученым и врачам более точно предсказывать и оптимизировать процессы, связанные с болезнями, что в конечном итоге приводит к улучшению результатов лечения и качества жизни пациентов.

Будущее математических моделей в онкологии

Математические модели роста злокачественных опухолей играют важную роль в онкологии, позволяя ученым и врачам лучше понять и предсказать развитие раковых заболеваний. Однако, будущее этих моделей в онкологии обещает быть еще более захватывающим и перспективным.

В первую очередь, развитие вычислительных технологий и доступность больших объемов данных позволяют создавать более точные и сложные математические модели роста опухолей. Модели могут учитывать множество факторов, таких как генетические особенности пациента, мутации опухолевых клеток, а также влияние окружающей среды.

Также, с развитием искусственного интеллекта и машинного обучения, математические модели могут стать еще более точными и предсказуемыми. Алгоритмы машинного обучения могут обрабатывать большие объемы данных и выявлять скрытые закономерности, которые могут помочь в определении наиболее эффективных методов лечения и предсказании результатов лечения пациентов.

Кроме того, математические модели могут быть использованы для оптимизации протоколов лечения и разработки индивидуальных подходов к каждому пациенту. Учитывая различные факторы, такие как возраст, пол и состояние здоровья пациента, модели могут помочь врачам выбрать наиболее эффективные методы лечения и предотвратить возможные осложнения.

И, наконец, математические модели могут быть использованы для исследования новых методов лечения и разработки новых препаратов. С их помощью можно проводить виртуальные эксперименты и предварительно оценить эффективность новых методов и лекарств на моделях опухолей, что сократит время и затраты на исследования.

Таким образом, будущее математических моделей в онкологии обещает быть ярким и перспективным. Они помогут ученым и врачам лучше понять и предсказать развитие раковых заболеваний, выбирать наиболее эффективные методы лечения и разрабатывать новые методы лечения и лекарства.