Математический класс какие предметы

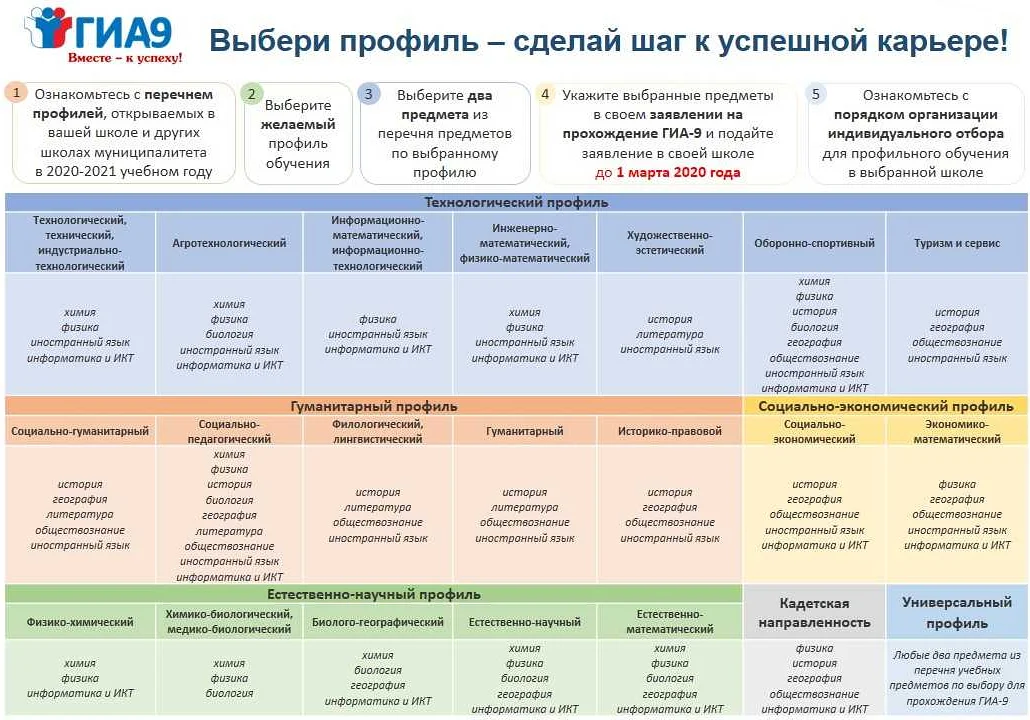
Математический класс включает в себя такие предметы, как алгебра, геометрия, математический анализ и теория вероятностей. Ученики в математическом классе изучают различные математические концепции и методы, развивают аналитическое мышление и умение решать сложные задачи. Математический класс предлагает учащимся глубокое погружение в мир математики и является основой для дальнейшего изучения научных и технических дисциплин.

Математика – один из основных предметов, которые включает программа обучения в математическом классе. Во время изучения математики ученики осваивают различные темы, такие как арифметика, геометрия, алгебра, тригонометрия и математический анализ. Математика является не только наукой, но и инструментом, который очень полезен в повседневной жизни и множестве профессий.

Еще одним важным предметом в математическом классе является физика. Физика – наука, которая изучает законы природы и объясняет феномены вокруг нас. Во время изучения физики студенты изучают такие темы, как механика, термодинамика, электромагнетизм и оптика. Физика помогает развить логическое мышление, умение анализировать и решать сложные задачи.

Еще одним важным предметом в программе обучения математического класса является информатика. Информатика – наука о обработке информации. Во время изучения информатики ученики узнают о компьютерных технологиях, программировании, алгоритмах и структурах данных. Эти навыки играют важную роль в современном мире, где информационные технологии становятся все более распространенными и востребованными.

Математический класс предоставляет студентам возможность развить свои навыки в области математики, физики и информатики. Эти предметы помогают ученикам развить логическое мышление, умение решать сложные задачи и применять полученные знания в повседневной жизни и карьере.

Математический класс: предметы программы обучения

Основными предметами в программе обучения математического класса являются:

1. Алгебра. В алгебре учат работать с алгебраическими выражениями, решать уравнения и неравенства, изучать функции и графики.
2. Геометрия. Геометрия позволяет ученикам изучать фигуры, пространственные отношения и свойства геометрических объектов.
3. Тригонометрия. Тригонометрия занимается изучением тригонометрических функций и их применением в различных задачах.
4. Математический анализ. Математический анализ включает в себя изучение пределов, производных и интегралов функций.
5. Вероятность и статистика. Этот предмет помогает учащимся изучать вероятностные модели и статистические данные, а также анализировать их.

Кроме основных предметов, в программу обучения математического класса также могут входить дополнительные предметы, такие как математическая логика, дискретная математика и математическая физика. Все эти предметы направлены на развитие математического мышления и подготовку учеников к дальнейшему изучению математики на более высоком уровне.

Алгебра: основа математического класса

В программе алгебры в математическом классе учащиеся изучают основные математические операции — сложение, вычитание, умножение и деление, а также работу с переменными и неизвестными. Они изучают различные алгебраические методы решения уравнений и неравенств, а также изучают графики и функции.

Одна из важных тем в программе алгебры — это работа с различными типами чисел, такими как натуральные числа, целые числа, рациональные числа и иррациональные числа. Учащиеся учатся распознавать эти типы чисел и выполнять операции с ними.

Алгебра также включает в себя изучение алгебраических выражений и алгебраических формул. Учащиеся учатся упрощать и умножать алгебраические выражения, а также решать уравнения и неравенства с использованием алгебраических формул.

Изучение алгебры в математическом классе помогает учащимся развить навыки критического мышления, аналитического мышления и проблемного мышления. Они учатся разбираться в сложных математических задачах, анализировать информацию и применять математические методы для решения проблем.

В итоге, изучение алгебры в математическом классе не только помогает учащимся развить навыки математического анализа, но и подготавливает их к изучению более сложных математических дисциплин в будущем.

Геометрия: изучение пространственных форм и фигур

В ходе изучения геометрии учащиеся осваивают основные понятия этой науки, такие как точка, прямая, плоскость, угол, треугольник, квадрат, окружность и другие. Они учатся классифицировать и описывать различные геометрические фигуры, а также находить их характеристические свойства.

Одним из важных разделов геометрии является изучение пространственных форм, таких как призма, пирамида, цилиндр, конус и шар. Учащиеся учатся определять их основные параметры, такие как высота, радиус, площадь поверхности и объем. Они также учатся решать задачи, связанные с расчетом этих параметров.

Геометрия важна не только для понимания и описания физического мира, но и для развития абстрактного и логического мышления учащихся. Она помогает им развить навыки анализа, рассуждения и решения проблем, которые могут быть применены не только в математике, но и в других областях жизни.

Изучение геометрии в математическом классе позволяет учащимся не только расширить свои знания о фигурах и формах, но и развить важные навыки и умения, необходимые для успешной учебы и дальнейшей жизни.

Тригонометрия: изучение связей между углами и сторонами

Основой тригонометрии являются тригонометрические функции, такие как синус, косинус и тангенс. Эти функции позволяют выразить отношения между сторонами и углами в треугольнике. Синус угла определяется как отношение противолежащей стороны к гипотенузе, косинус угла – как отношение прилежащей стороны к гипотенузе, а тангенс угла – как отношение противолежащей стороны к прилежащей стороне.

Изучение тригонометрии позволяет решать различные задачи, связанные с треугольниками, такие как определение неизвестных сторон или углов, нахождение площади треугольника, решение задач на проведение высоты, медианы или биссектрисы треугольника и т. д.

Тригонометрия является основой для более сложных математических разделов, таких как аналитическая геометрия, дифференциальное и интегральное исчисления, физика и другие науки. Поэтому изучение тригонометрии в рамках математического класса является важным шагом в математическом образовании.

В процессе обучения тригонометрии студенты изучают различные свойства и теоремы, связанные с углами и сторонами треугольников, решают задачи, проводят измерения и анализируют результаты. Это помогает им развивать навыки логического мышления, аналитического мышления и применения математических знаний в практических ситуациях.

Тригонометрия является важной и полезной математической дисциплиной, которая находит применение в различных областях науки, техники и технологии. Поэтому изучение тригонометрии в математическом классе является необходимым компонентом образования, который помогает подготовить студентов к дальнейшему изучению математики и применению ее знаний в реальной жизни.

Математический анализ: изучение пределов и производных

Изучение пределов является одной из важных тем в математическом анализе. Предел функции определяет ее поведение при стремлении аргумента к определенному значению. Изучение пределов позволяет понять, как функция ведет себя в окрестности определенной точки и как она изменяется при приближении к этой точке.

Производная функции является одной из основных характеристик функции. Она показывает скорость изменения функции в каждой точке ее области определения. Изучение производных позволяет решать задачи оптимизации, находить экстремумы функции, исследовать ее поведение и многое другое.

В процессе изучения математического анализа студенты ознакамливаются с основными определениями и свойствами пределов и производных, учатся применять соответствующие методы и приемы для решения различных задач. Важной частью обучения является решение практических задач и исследование различных функций.

Математический анализ является базой для дальнейшего изучения математических и естественнонаучных дисциплин. Он также находит широкое применение в прикладных областях, таких как физика, экономика, биология и др.

Математическая статистика: анализ данных и вероятность

Анализ данных в математической статистике включает в себя сбор, описание, представление и интерпретацию данных. С помощью различных статистических методов и техник, статистики могут изучать свойства выборок, выявлять закономерности и зависимости между переменными, а также проверять гипотезы и делать прогнозы.

Вероятность — это важная составная часть математической статистики. Она изучает случайные события и их вероятности. При помощи теории вероятностей можно оценить вероятность наступления определенного события и предсказать его исходы. Вероятность используется для построения моделей, прогнозирования и принятия решений на основе данных.

Понимание и применение математической статистики позволяет ученикам развивать аналитическое мышление, умение работать с данными и применять математические методы для решения реальных задач. Эти навыки являются важными как в научной сфере, так и в практической деятельности, например, в экономике, финансах, медицине и социальных науках.

Дискретная математика: изучение алгоритмов и логики

Изучение алгоритмов является одним из ключевых аспектов дискретной математики. Студенты учатся разрабатывать, анализировать и оптимизировать алгоритмы различной сложности. Они изучают методы сортировки, поиска, графов и другие алгоритмические структуры данных. Важным аспектом изучения алгоритмов является оценка их эффективности и сложности.

Еще одним важным аспектом дискретной математики является изучение логики. Студенты учатся анализировать и оценивать логические выражения и доказывать различные математические утверждения. Они изучают основные принципы логики, такие как законы Де Моргана, импликация и доказательства.

В рамках изучения дискретной математики студенты также знакомятся с другими темами, такими как комбинаторика, теория графов, теория вероятностей и математическая логика. Все эти предметы позволяют разработать у студентов навыки абстрактного мышления, логического анализа и решения сложных задач.

Основные темы дискретной математикиПримеры

Алгоритмы	Сортировка пузырьком, поиск в глубину
Логика	Доказательства математических утверждений
Комбинаторика	Расчет количества комбинаций и перестановок
Теория графов	Анализ свойств графов и поиск кратчайшего пути
Теория вероятностей	Расчет вероятности событий и условных вероятностей

Изучение дискретной математики в математическом классе позволяет студентам развить свои навыки в области алгоритмов и логики, что является важным для решения различных задач в науке, технологии и других областях деятельности.

Теория чисел: исследование свойств и взаимосвязей чисел

Основные темы, изучаемые в рамках теории чисел, включают:

Теория делимости	Исследование условий, при которых одно число делится на другое без остатка. Рассматриваются такие понятия, как наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) двух чисел.
Простые числа	Анализ особенностей и свойств простых чисел. Изучаются простые числа-близнецы (пары чисел, разность между которыми равна двум), теорема Вильсона, теорема Ферма и другие теоремы, связанные с простыми числами.
Конгруэнции	Изучение свойств чисел, сравнимых по модулю. Рассматриваются конгруэнтные уравнения, китайская теорема об остатках и другие теоремы, основанные на понятии конгруэнции.
Криптография	Применение теории чисел в области защиты информации. Изучаются методы шифрования, основанные на сложности факторизации больших чисел, асимметричные криптосистемы и другие аспекты криптографии.
Арифметика Ферма	Исследование свойств и особенностей решений диофантовых уравнений, в частности, уравнения x^n + y^n = z^n, где n > 2. Эта область теории чисел тесно связана с алгеброй и геометрией.

Теория чисел имеет много практических приложений, включая криптографию, оптимизацию алгоритмов, разработку компьютерных систем и другие области. Углубленное изучение теории чисел позволяет понять множество интересных свойств чисел и применить их на практике.

Вопрос-ответ:

Какие предметы включает программа обучения в математическом классе?

Программа обучения в математическом классе включает такие предметы, как алгебра, геометрия, математический анализ, теория вероятностей и математическая статистика.

Какие знания и умения формируются у учеников в математическом классе?

В математическом классе ученики формируют знания и умения в области алгебры, геометрии, математического анализа, теории вероятностей и математической статистики. Они учатся решать уравнения и неравенства, проводить геометрические построения, анализировать функции, работать с матрицами и векторами, изучать пространства и многое другое.

Какие навыки развиваются у учеников в математическом классе?

В математическом классе ученики развивают навыки логического мышления, аналитического мышления, абстрактного мышления, критического мышления, решения проблем, коммуникации и коллаборации. Они учатся анализировать информацию, формулировать и проверять гипотезы, находить решения для сложных задач, обосновывать свои выводы и работать в команде.

Какие методы обучения используются в математическом классе?

В математическом классе используются различные методы обучения, такие как лекции, практические занятия, индивидуальные задания, групповые проекты, решение задач, проведение экспериментов, использование компьютерных программ и интерактивных учебников. Это позволяет ученикам получать знания и навыки через разнообразные активности и подходы.

Какие возможности открывает изучение математики в школе?

Изучение математики в школе открывает ученикам множество возможностей. Они могут применять математические знания и навыки в реальной жизни, в науке, в технике, в экономике. Они могут продолжить образование в области математики на университетском уровне и выбрать профессию, связанную с математикой, такую как программист, инженер, экономист, ученый и другие.

Видео по теме: