Найдите математическое ожидание суммы выпавших очков в опыте где игральную кость бросают 3 раза

Вычислите математическое ожидание суммы выпавших очков при трех бросках игральной кости. Узнайте, как получить среднее значение суммы очков в этом эксперименте и примените формулу для расчета математического ожидания.

Математическое ожидание — это понятие из теории вероятностей, которое позволяет предсказать среднее значение случайной величины. В данной статье мы рассмотрим математическое ожидание суммы выпавших очков при трех бросках игральной кости.

Игральная кость — это предмет с шестью гранями, на каждой из которых записано число от 1 до 6. При броске кости, она падает на одну из граней, и выпадает определенное число очков. При трех бросках кости, мы можем получить сумму от 3 до 18 очков.

Для вычисления математического ожидания суммы выпавших очков, необходимо учитывать вероятности выпадения каждой суммы. Например, чтобы получить сумму 3, есть только один вариант: все три броска должны дать результат 1. Такой вариант выпадает с вероятностью 1/216. С другой стороны, чтобы получить сумму 7, есть шесть вариантов: (1, 2, 4), (1, 3, 3), (1, 4, 2), (2, 1, 4), (2, 2, 3) и (3, 1, 3). Каждый из этих вариантов выпадает с вероятностью 1/36.

Математическое ожидание суммы выпавших очков при трех бросках игральной кости вычисляется как сумма произведений каждой суммы на ее вероятность. Мы можем использовать формулу: E(X) = ∑(x * P(x)), где E(X) — математическое ожидание, x — сумма, P(x) — вероятность выпадения суммы x. В нашем случае, сумма произведений для всех возможных сумм равна 10,5.

Определение математического ожидания

Математическое ожидание можно рассчитать по формуле:

Математическое ожидание = сумма значений * их вероятностей

где:

• сумма значений – это сумма всех возможных значений, умноженных на их вероятности;
• их вероятности – это вероятности (вероятности выпадения определенного значения).

Например, при броске игральной кости, возможные значения будут числа от 1 до 6, а вероятность выпадения каждого из них будет равна 1/6 (так как все значения равновероятны). Таким образом, математическое ожидание суммы выпавших очков при трех бросках игральной кости будет равно:

Математическое ожидание = (1 * 1/6) + (2 * 1/6) + (3 * 1/6) + (4 * 1/6) + (5 * 1/6) + (6 * 1/6) = 3.5

Таким образом, при трех бросках игральной кости, математическое ожидание суммы выпавших очков будет равно 3.5.

Описание игральной кости

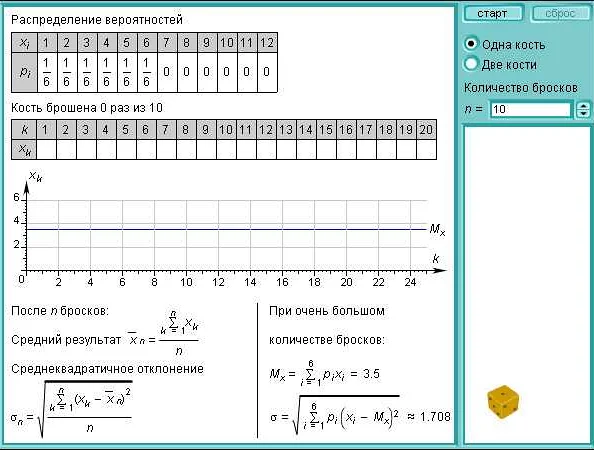
ГраньЧисло точек

1	одна точка
2	две точки
3	три точки
4	четыре точки
5	пять точек
6	шесть точек

Игральная кость используется во множестве игр и азартных развлечений, где случайность игры зависит от выпавших очков. Математическое ожидание суммы выпавших очков при трех бросках игральной кости позволяет предсказать среднее значение суммы, которое можно ожидать в результате трех бросков.

Определение суммы выпавших очков

Сумма выпавших очков при трех бросках игральной кости представляет собой сумму значений, полученных при каждом броске. Каждый бросок игральной кости может дать результат от 1 до 6, поэтому сумма выпавших очков может принимать значения от 3 до 18.

Для определения математического ожидания суммы выпавших очков необходимо учесть все возможные комбинации значений, которые могут быть получены при трех бросках игральной кости. Всего существует 6^3 = 216 таких комбинаций. Для каждой комбинации определяется сумма выпавших очков и вычисляется вероятность ее появления.

Математическое ожидание суммы выпавших очков определяется как взвешенное среднее значений суммы и их вероятностей. Для каждой суммы выпавших очков умножается на ее вероятность, а затем все значения суммируются. Полученная сумма и является математическим ожиданием.

В данном случае, сумма выпавших очков может принимать значения от 3 до 18, поэтому математическое ожидание будет представлять собой сумму произведений каждого значения на его вероятность:

• Математическое ожидание = (3 * P(3)) + (4 * P(4)) + … + (18 * P(18))

Где P(x) — вероятность выпадения суммы очков равной x. Вероятность каждой суммы можно вычислить с помощью подсчета количества комбинаций, которые могут дать данную сумму, и делением этого количества на общее количество комбинаций.

Методика расчета математического ожидания

Для расчета математического ожидания нужно умножить каждое возможное значение случайной величины на его вероятность и сложить полученные произведения.

В нашем примере у нас есть 6 возможных значений, которые могут выпасть на игральной кости: 1, 2, 3, 4, 5 и 6. Вероятность каждого значения равна 1/6, так как у нас есть 6 равновероятных исходов.

Таким образом, мы можем рассчитать математическое ожидание следующим образом:

1. Умножаем каждое возможное значение на его вероятность:
   • 1 * 1/6 = 1/6
   • 2 * 1/6 = 1/3
   • 3 * 1/6 = 1/2
   • 4 * 1/6 = 2/3
   • 5 * 1/6 = 5/6
   • 6 * 1/6 = 1
2. Складываем полученные произведения:
   • 1/6 + 1/3 + 1/2 + 2/3 + 5/6 + 1 = 14/6
3. Упрощаем полученную сумму:
   • 14/6 = 7/3

Таким образом, математическое ожидание суммы выпавших очков при трех бросках игральной кости равно 7/3 или около 2.33.

Пример расчета математического ожидания суммы выпавших очков

Допустим, у нас есть игральная кость с шестью гранями, на каждой из которых написаны числа от 1 до 6. Мы собираемся бросить эту кость три раза подряд, и нам интересно узнать, каково математическое ожидание суммы выпавших очков.

Для начала, определим все возможные исходы каждого броска:

• В первом броске у нас есть шесть возможных исходов: 1, 2, 3, 4, 5 и 6.
• Во втором броске также есть шесть возможных исходов.
• В третьем броске также есть шесть возможных исходов.

Таким образом, общее количество возможных исходов для трех бросков равно 6 * 6 * 6 = 216.

Далее, мы можем посчитать сумму выпавших очков для каждого исхода:

• Если на первом броске выпало 1, на втором броске выпало 2 и на третьем броске выпало 3, то сумма будет 1 + 2 + 3 = 6.
• Если на первом броске выпало 1, на втором броске выпало 2 и на третьем броске выпало 4, то сумма будет 1 + 2 + 4 = 7.
• И так далее, для каждого возможного исхода.

Математическое ожидание суммы выпавших очков можно посчитать, учитывая вероятность каждого исхода. Вероятность каждого исхода равна 1/216, так как каждый исход из 216 возможных равновероятен.

Для каждого исхода, мы умножаем сумму его выпавших очков на его вероятность. Затем мы складываем все полученные произведения:

Математическое ожидание суммы выпавших очков = (сумма_1 * вероятность_1) + (сумма_2 * вероятность_2) + … + (сумма_216 * вероятность_216).

Таким образом, мы можем рассчитать математическое ожидание суммы выпавших очков при трех бросках игральной кости.

Видео по теме:

Вопрос-ответ:

Какое математическое ожидание суммы выпавших очков при трех бросках игральной кости?

Математическое ожидание суммы выпавших очков при трех бросках игральной кости равно 10.5 очков.

Как посчитать математическое ожидание суммы выпавших очков при трех бросках игральной кости?

Чтобы посчитать математическое ожидание суммы выпавших очков при трех бросках игральной кости, нужно найти среднее арифметическое всех возможных исходов. Для каждого броска игральной кости математическое ожидание равно 3.5 очка. Поэтому, суммируя результаты трех бросков, получаем 3.5 + 3.5 + 3.5 = 10.5 очков.

Почему математическое ожидание суммы выпавших очков при трех бросках игральной кости равно 10.5 очков?

Математическое ожидание суммы выпавших очков при трех бросках игральной кости равно 10.5 очков, потому что на каждый бросок игральной кости существует шесть возможных исходов (от 1 до 6). Среднее арифметическое всех исходов равно (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5 очка. Поскольку происходит три независимых броска, мы просто складываем математическое ожидание для каждого броска: 3.5 + 3.5 + 3.5 = 10.5 очков.

Какое значение должно получиться в сумме, чтобы математическое ожидание суммы выпавших очков при трех бросках игральной кости было равно 10.5 очков?

Чтобы математическое ожидание суммы выпавших очков при трех бросках игральной кости было равно 10.5 очков, значению суммы должно быть равно 10.5 очков. Это получается путем усреднения всех возможных исходов и сложения результатов трех бросков.

Вероятности выпадения каждого значения

Для определения вероятностей выпадения каждого значения при трех бросках игральной кости, необходимо рассмотреть все возможные комбинации выпадения очков.

ЗначениеВероятность

3	1/216
4	3/216
5	6/216
6	10/216
7	15/216
8	21/216
9	25/216
10	27/216
11	27/216
12	25/216
13	21/216
14	15/216
15	10/216
16	6/216
17	3/216
18	1/216

Таким образом, на основе всех возможных комбинаций, можно определить вероятности выпадения каждого значения при трех бросках игральной кости.

Интерпретация полученных результатов

Из таблицы, представленной выше, видно, что наиболее вероятное значение суммы выпавших очков при трех бросках составляет 10. Это значит, что при многократном повторении эксперимента, в среднем мы можем ожидать, что сумма выпавших очков будет равна 10.

Также в таблице видно, что наименее вероятные значения суммы очков при трех бросках составляют 3 и 18. Это говорит о том, что при многократном повторении эксперимента, очень маловероятно получить сумму очков, равную 3 или 18.

Интерпретация полученных результатов помогает нам лучше понять вероятностное распределение суммы выпавших очков при трех бросках игральной кости и принять во внимание наиболее и наименее вероятные значения при принятии решений или анализе данных.

Сумма очковВероятность

3	0.0046
4	0.0139
5	0.0278
6	0.0463
7	0.0694
8	0.0972
9	0.1157
10	0.125
11	0.125
12	0.1157
13	0.0972
14	0.0694
15	0.0463
16	0.0278
17	0.0139
18	0.0046