Математика 10 класс что проходят

В этой статье вы узнаете, какие темы изучаются в 10 классе математики: алгебра, геометрия, тригонометрия, статистика и вероятность. Мы рассмотрим основные понятия и методы решения задач, которые входят в программу 10 класса. Подробный обзор материала поможет вам успешно подготовиться к экзамену.

Математика является одним из самых фундаментальных предметов в школьной программе. В 10 классе ученики углубляют свои знания и навыки, изучая новые темы и концепции. В этой статье мы рассмотрим основные темы и понятия, которые изучаются в 10 классе.

Одной из ключевых тем в 10 классе является алгебра. Ученики изучают различные алгебраические операции, включая сложение, вычитание, умножение и деление полиномов. Они также изучают системы линейных уравнений и методы их решения, такие как метод подстановки и метод графического представления.

Важные понятия в алгебре включают понятие переменной и функции. Ученики узнают, как определять переменные и решать уравнения с одной или несколькими переменными. Они также изучают функции и их свойства, такие как область определения, область значений и график функции.

Еще одной важной темой, изучаемой в 10 классе, является геометрия. Ученики углубляют свои знания о геометрических фигурах, таких как треугольники, квадраты и окружности, а также о свойствах их сторон и углов. Они также изучают теоремы и свойства треугольников, включая теоремы Пифагора и Талеса.

Арифметика и основные операции

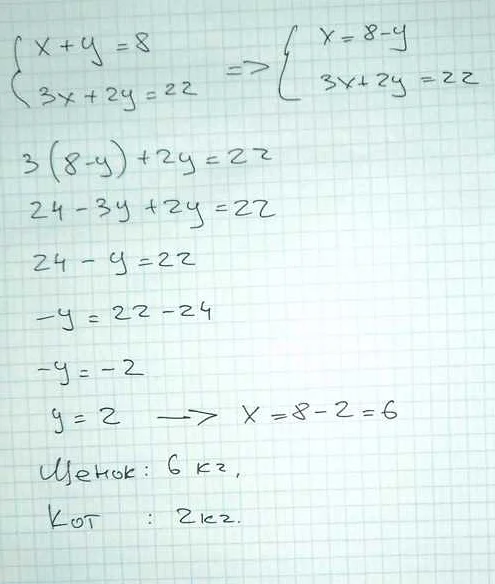
Сложение — это операция, при которой два или более числа суммируются, чтобы получить их сумму. Сложение обозначается знаком «+». Например, 2 + 3 = 5.

Вычитание — это операция, при которой из одного числа вычитается другое число, чтобы получить разность. Вычитание обозначается знаком «-«. Например, 5 — 3 = 2.

Умножение — это операция, при которой одно число умножается на другое число, чтобы получить произведение. Умножение обозначается знаком «×» или «*». Например, 2 × 3 = 6.

Деление — это операция, при которой одно число делится на другое число, чтобы получить частное. Деление обозначается знаком «÷» или «/». Например, 6 ÷ 3 = 2.

Кроме основных операций, в арифметике также используются дополнительные операции, такие как возведение в степень и извлечение корня. Возведение в степень обозначается знаком «^» или «**», а извлечение корня обозначается символом «√». Например, 2^3 = 8 и √9 = 3.

Знание арифметики и основных операций является основой для решения различных математических задач и является необходимым навыком для понимания более сложных тем в математике.

Видео по теме:

Геометрия: фигуры и их свойства

Одна из основных геометрических фигур – это треугольник. Треугольник имеет три стороны и три угла. В зависимости от длин сторон и величин углов, треугольники могут быть равнобедренными, равносторонними, прямоугольными и т.д.

Другая геометрическая фигура – это четырехугольник. Четырехугольник имеет четыре стороны и четыре угла. Прямоугольник и квадрат – это особые виды четырехугольников. У прямоугольника все углы прямые, а у квадрата все стороны равны.

Круг – это геометрическая фигура, которая состоит из всех точек плоскости, находящихся на одинаковом расстоянии от центра. У круга есть радиус (расстояние от центра до любой точки на окружности) и диаметр (расстояние между любыми двумя точками на окружности, через центр).

Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны. У параллелограмма также равны противоположные углы.

Это лишь некоторые из геометрических фигур и их свойств, изучаемых в 10 классе. Знание этих фигур и понимание их свойств помогает ученикам анализировать и решать различные геометрические задачи.

Алгебра: уравнения и неравенства

Решение уравнений и неравенств – это процесс нахождения всех значений неизвестной величины, при которых исходное уравнение или неравенство выполняется. Для решения уравнений и неравенств используются различные методы, такие как метод подстановки, метод приведения подобных, метод графического представления и др.

Уравнения и неравенства встречаются в различных областях математики и позволяют решать широкий спектр задач. Они используются для нахождения неизвестных величин, построения графиков функций, определения интервалов изменения переменных и др.

При изучении уравнений и неравенств важно уметь анализировать условия задачи, правильно записывать уравнения и неравенства, а также проводить логические операции с ними. Навыки решения уравнений и неравенств помогут студентам развить логическое мышление и решать сложные задачи в различных областях науки и техники.

Изучение алгебры и решение уравнений и неравенств является важной частью школьной программы по математике и подготавливает учеников к дальнейшему изучению более сложных математических тем на уровне старших классов и высшего образования.

Функции и их графики

График функции – это геометрическое представление функции на плоскости. Он позволяет наглядно изучать изменение значений функции в зависимости от аргумента.

График функции может иметь различные формы, которые свидетельствуют о ее свойствах. Например, график возрастающей функции будет подниматься вверх от левого к правому краю, а график убывающей функции – опускаться.

Кроме того, графики функций могут пересекаться или не пересекаться, иметь точки экстремума, асимптоты и различные другие характеристики. Изучение графиков функций помогает понять их свойства и использовать их в различных математических задачах.

Тригонометрия: синус, косинус, тангенс

Синус угла в прямоугольном треугольнике определяется как отношение противолежащего катета к гипотенузе: sin(α) = a / c.

Косинус угла в прямоугольном треугольнике определяется как отношение прилежащего катета к гипотенузе: cos(α) = b / c.

Тангенс угла в прямоугольном треугольнике определяется как отношение противолежащего катета к прилежащему катету: tg(α) = a / b.

Значения синуса, косинуса и тангенса углов можно найти с помощью таблицы тригонометрических значений или с помощью калькулятора.

Угол (α)Синус (sin(α))Косинус (cos(α))Тангенс (tg(α))

0°	0	1	0
30°	1/2	√3/2	√3/3
45°	√2/2	√2/2	1
60°	√3/2	1/2	√3
90°	1	0	∞

Тригонометрические функции широко применяются в геометрии, физике, инженерии и других науках для решения задач, связанных с углами и треугольниками. Знание синуса, косинуса и тангенса позволяет вычислять длины сторон треугольников, находить углы по известным сторонам и многое другое.

Вероятность и статистика

Вероятность — это величина, которая оценивает шансы на наступление определенного события. Она изучает вероятность различных исходов и помогает нам принимать решения на основе этих вероятностей. Примерами задач, связанных с вероятностью, могут быть определение вероятности выпадения определенного числа на игральной кости или вероятности выигрыша в лотерее.

Статистика, с другой стороны, изучает коллективные данные и использует их для извлечения информации и принятия выводов. Она помогает нам анализировать и интерпретировать данные, собранные из различных источников. Например, статистика может быть использована для анализа результатов опросов, изучения тенденций в экономике или прогнозирования будущих событий на основе исторических данных.

Вероятность и статистика тесно связаны между собой и часто используются вместе для решения различных задач. Например, статистика может использовать вероятность для анализа данных и определения значимости результатов. Вероятность же может использоваться для предсказания будущих событий на основе статистических данных.

Изучение вероятности и статистики позволяет развить способность к анализу и критическому мышлению. Эти навыки могут быть полезными во многих областях жизни, включая научные исследования, экономику, финансы, медицину и многие другие.

Математическая логика и доказательства

Основные понятия математической логики включают понятия высказывания, истинности и логических операций. Высказывание — это утверждение, которое может быть либо истинным, либо ложным. Логические операции, такие как отрицание, конъюнкция, дизъюнкция и импликация, позволяют нам строить более сложные высказывания на основе простых.

Одна из основных задач математической логики — это доказательство. Доказательство — это логическая последовательность высказываний, которая приводит к выводу истинности некоторого утверждения. Доказательство может быть построено с использованием аксиом, определений и ранее доказанных теорем.

Существует несколько методов доказательства, включая прямое доказательство, доказательство от противного, математическую индукцию и доказательство существования. Каждый из этих методов имеет свои особенности и применяется в разных ситуациях.

Математическая логика и доказательства играют важную роль в различных областях математики, а также в компьютерных науках и философии. Они позволяют строить строгие и надежные рассуждения, а также формализовать и анализировать сложные математические структуры и системы.

Изучение математической логики и доказательств помогает развить навыки логического мышления, а также способность анализировать и решать проблемы. Эти навыки могут быть полезными не только в математике, но и в других областях жизни, где требуется логическое и аналитическое мышление.

Математические модели и задачи

Математические модели могут быть представлены в виде алгебраических уравнений, дифференциальных уравнений, статистических формул и других математических конструкций. Они позволяют описывать различные процессы и явления, такие как движение тел, распределение вероятностей, рост популяции и многое другое.

Для решения задач с использованием математических моделей необходимо сформулировать их в математической форме и затем применить соответствующие методы и техники для получения решения. Для этого может потребоваться применение различных математических дисциплин, таких как алгебра, геометрия, теория вероятностей и другие.

Решение задач с использованием математических моделей позволяет получить количественные и качественные характеристики рассматриваемых явлений и систем. Оно позволяет проводить анализ, прогнозирование и оптимизацию процессов, а также принимать обоснованные решения на основе полученных результатов.

Примеры задач, решаемых с помощью математических моделей:

1. Моделирование распределения вероятностей в экспериментах с игральными костями.

2. Расчет траектории полета снаряда при различных начальных условиях.

3. Оптимизация расписания поездов с учетом ограничений по времени и пропускной способности пути.

4. Прогнозирование изменения цен на финансовых рынках с использованием статистических моделей.

Математические модели и задачи являются важной частью математического образования и научного исследования. Они позволяют применять математические методы и инструменты для решения реальных проблем и развивать математическое мышление и навыки анализа.

Вопрос-ответ:

Какие темы изучаются в 10 классе по математике?

В 10 классе по математике изучаются такие темы, как тригонометрия, вероятность, аналитическая геометрия, функции и их свойства, производные и интегралы.

Какие основные понятия изучаются в 10 классе по математике?

В 10 классе по математике изучаются такие основные понятия, как тригонометрические функции, вероятность событий, уравнения и неравенства, производные и интегралы функций.

Чему посвящена тема аналитической геометрии в 10 классе?

Тема аналитической геометрии в 10 классе посвящена изучению координатных преобразований, уравнений прямых и плоскостей, а также решению геометрических задач с использованием алгебраических методов.

Какие функции изучаются в 10 классе по математике?

В 10 классе по математике изучаются такие функции, как линейные, квадратные, показательные, логарифмические и тригонометрические функции.

Зачем изучать производные и интегралы в 10 классе?

Изучение производных и интегралов в 10 классе позволяет понять основные понятия математического анализа и их применение в решении различных задач, а также подготовиться к дальнейшему изучению математики в старших классах и вузе.