Математика 3 это когда

Математика 3 это когда ученики изучают основные понятия алгебры, геометрии и математического анализа. В этом возрасте дети начинают изучать различные математические операции, решать уравнения и задачи на геометрическую конструкцию. Математика 3 помогает развить логическое мышление, абстрактное мышление и аналитические навыки учеников. Чтобы успешно изучать математику 3, необходимо иметь хорошее понимание чисел, операций с ними и базовых геометрических понятий.

Математика – это наука, изучающая структуру, свойства и отношения чисел, пространств, структур и изменений. Она является одной из самых древних наук и является основой для множества других научных и технических дисциплин.

Математика 3 – это продолжение изучения математики после школьного курса. В этом курсе студенты углубляются в изучение таких разделов математики, как алгебра, геометрия, теория вероятностей и математическая статистика.

Студенты, изучающие математику 3, получают более глубокие и расширенные знания в области математической логики, алгебраических структур, теории множеств и математического анализа. Они также изучают применение математики в различных областях, таких как физика, экономика, компьютерные науки и промышленность.

Математика 3 играет важную роль в развитии аналитического мышления, логического мышления и критического мышления студентов. Она помогает развить навыки решения сложных задач, анализировать данные и принимать обоснованные решения. Кроме того, математика 3 является фундаментом для дальнейшего изучения и применения математики в научных и технических областях.

Разделение чисел и операции с ними

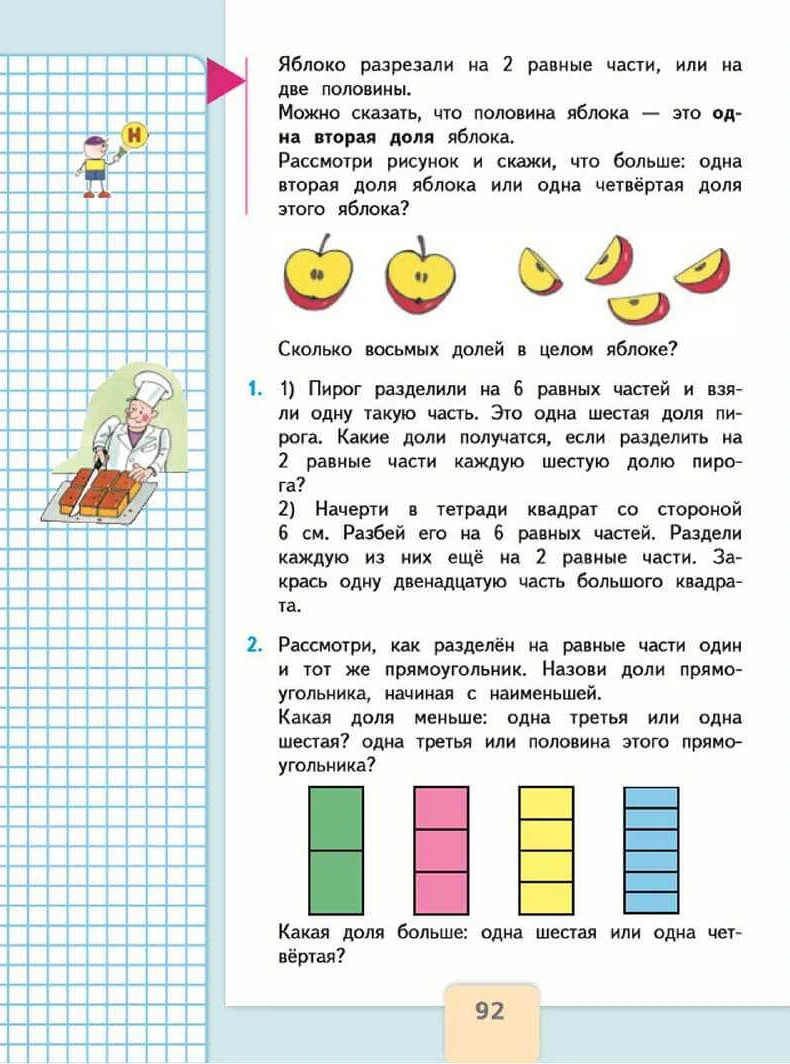
Для разделения чисел используется знак деления «/», который обозначает операцию деления. Например, если мы хотим разделить число 10 на 2, мы записываем это как 10 / 2. Результатом этой операции будет число 5.

Операция деления также может быть представлена в виде дроби. Например, 10 / 2 может быть записано как 10:2 или как 10 ÷ 2. Оба этих способа обозначают одну и ту же операцию.

В математике также используется понятие остатка от деления. Остаток от деления обозначает то, что остается после того, как одно число не делится на другое нацело. Например, при делении числа 10 на 3, результат будет 3 и остаток 1. Это можно записать как 10 ÷ 3 = 3, остаток 1.

Кроме разделения чисел, с помощью операции деления можно выполнять и другие математические операции, такие как умножение и вычитание.

Умножение числа на дробь — это то же самое, что и разделение числа на обратную дробь. Например, если мы хотим умножить число 5 на 1/2, мы можем записать это как 5 · 1/2, что равно 5 / 2 или 2,5.

Вычитание числа из другого числа также может быть представлено как разделение числа на обратное число. Например, если мы хотим вычесть число 3 из числа 7, мы можем записать это как 7 — 3, что равно 7 / (-3) или -2.

Операция деления и соответствующие ей математические операции широко используются в различных областях математики, науки и повседневной жизни.

Понятие и применение десятичных дробей

Десятичные дроби имеют десятичную точку, которая отделяет целую часть числа от его дробной части. Например, в числе 3.14, 3 — это целая часть, а 14 — это дробная часть.

Десятичные дроби широко используются в повседневной жизни и в различных областях, таких как финансы, наука, инженерия и технологии. Они позволяют точно представлять и вычислять дробные значения и доли вещественных величин.

Десятичные дроби могут быть представлены в различных форматах, таких как конечные десятичные дроби и периодические десятичные дроби. Конечные десятичные дроби имеют ограниченное количество цифр после запятой, например, 0.25. Периодические десятичные дроби имеют повторяющуюся последовательность цифр после запятой, например, 0.3333…

Понимание и умение работать с десятичными дробями является важным навыком в математике. Оно позволяет производить точные вычисления, а также анализировать и интерпретировать данные, представленные в виде десятичных дробей.

Десятичные дроби используются во многих математических операциях, таких как сложение, вычитание, умножение и деление. Они также используются для решения задач, связанных с долями, процентами, вероятностями и различными масштабами измерений.

В заключение, понятие и применение десятичных дробей являются неотъемлемой частью математики и имеют широкое применение в реальном мире. Они позволяют точно представлять и работать с дробными значениями, что является необходимым для различных областей знаний и практических задач.

Геометрия и ее основные принципы

Основные принципы геометрии включают в себя:

1. Пространственные отношения: Геометрия изучает взаимное расположение объектов в пространстве. Это включает в себя понятия расстояния, угла, направления и движения.

2. Формы и фигуры: Геометрия определяет различные формы и фигуры, такие как прямоугольник, круг, треугольник и т. д. Она помогает нам классифицировать и описывать эти формы, а также исследовать их свойства и взаимосвязи.

3. Координатная система: Геометрия использует координатную систему для определения точек в пространстве. Координаты (x, y, z) позволяют нам точно указывать положение объектов и измерять расстояния между ними.

4. Преобразования и симметрия: Геометрия изучает преобразования, такие как поворот, сдвиг и отражение, которые изменяют форму и положение объектов. Она также исследует симметрию, которая является важным аспектом геометрии и встречается в природе и искусстве.

5. Аксиомы и доказательства: Геометрия строится на основе аксиом, которые принимаются без доказательства. Используя логическое рассуждение, геометрия может выводить новые факты и утверждения из этих аксиом, что позволяет нам лучше понять свойства и отношения объектов.

Изучение геометрии развивает наше пространственное мышление, способность решать проблемы и анализировать информацию. Она применяется в различных областях, таких как архитектура, инженерия, физика, компьютерная графика и многое другое.

Понимание основных принципов геометрии позволяет нам лучше понять окружающий мир и использовать его в своих практических задачах и исследованиях.

Алгебраические выражения и их использование

Алгебраическое выражение представляет собой комбинацию чисел, переменных и математических операций, таких как сложение, вычитание, умножение и деление. Оно используется для описания отношений между величинами и решения различных математических задач.

Алгебраические выражения могут быть простыми, состоящими из одной переменной или числа, или составными, состоящими из нескольких частей, соединенных математическими операторами. Примеры простых алгебраических выражений: 2x, 3y, 5. Примеры составных алгебраических выражений: 2x + 3y, 4x — 2y.

Алгебраические выражения могут использоваться для решения различных математических задач. Например, они могут использоваться для нахождения неизвестных переменных в уравнениях, для нахождения значений функций, для моделирования реальных ситуаций и т. д. Использование алгебраических выражений позволяет упростить и анализировать математические задачи, делая их более понятными и решаемыми.

Операции, которые можно выполнять с алгебраическими выражениями, включают сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Также можно применять различные правила алгебры для упрощения выражений, сокращения их до более простых форм.

Вывод и использование алгебраических выражений являются важными навыками в математике. Они позволяют нам анализировать и решать различные математические задачи, а также применять математические понятия в реальных ситуациях. Поэтому важно понимать основные понятия и правила использования алгебраических выражений.

Решение уравнений и систем уравнений

Для решения уравнений необходимо найти значения переменных, при которых уравнение становится верным. Существует несколько методов решения уравнений, таких как алгебраический метод, метод подстановки и графический метод. В зависимости от сложности уравнения выбирается подходящий метод решения.

Система уравнений представляет собой набор двух или более уравнений, которые должны выполняться одновременно. Решение системы уравнений осуществляется путем нахождения значений переменных, при которых все уравнения системы становятся верными одновременно.

Для решения систем уравнений применяются различные методы, такие как метод сложения, метод вычитания, метод замены и метод графического решения. Каждый из этих методов имеет свои особенности и применяется в зависимости от сложности системы.

Решение уравнений и систем уравнений является важным этапом в многих областях науки и техники, таких как физика, химия, экономика и многих других. Умение решать уравнения и системы уравнений позволяет находить решения задач и принимать обоснованные решения.

Понятие и применение процентов

Проценты активно применяются в финансовом секторе, в банковской сфере, в торговле и бизнесе. Они помогают рассчитать прибыль, налоги, скидки, процентные ставки и многое другое.

Проценты также широко используются в статистике и анализе данных. Например, в маркетинге используется понятие конверсии — процента людей, которые совершают определенное действие, такое как покупка товара или подписка на услугу.

В повседневной жизни мы также сталкиваемся с процентами. Например, при расчете скидок в магазине или при определении процента роста нашей инвестиции.

Понимание процентов и умение применять их в различных ситуациях является важным навыком, который помогает нам принимать осознанные решения и понимать финансовые и статистические данные.

Статистика и ее применение на практике

Одним из ключевых понятий в статистике является понятие выборки. Выборка – это подмножество элементов из генеральной совокупности, которое представляет собой объект анализа. Например, при исследовании мнения населения о политических предпочтениях, выборка может состоять из нескольких тысяч человек.

Как только выборка собрана, статистики могут применять различные методы для анализа данных. Одним из основных методов является построение таблиц и диаграмм. Таблицы помогают организовать данные и сделать их более понятными, а диаграммы позволяют визуализировать информацию.

ГородКоличество жителей

Москва	12 678 079
Санкт-Петербург	5 383 890
Новосибирск	1 613 833

С помощью таблицы можно сравнить количество жителей разных городов и сделать выводы о их населении.

Статистика также позволяет проводить различные статистические тесты, такие как t-тесты и анализ дисперсии, для проверки гипотез. Например, статистический тест может показать, есть ли статистически значимая разница в среднем доходе мужчин и женщин.

Еще одной важной областью применения статистики является прогнозирование. С помощью статистических методов можно предсказывать будущие события на основе имеющихся данных. Например, статистика может использоваться для прогнозирования экономического роста или спроса на товары и услуги.

В современном мире, где данные являются ценным ресурсом, понимание статистики и умение применять ее на практике становятся все более важными навыками. Они позволяют принимать обоснованные решения на основе фактов и анализа, что способствует развитию и успеху в различных областях деятельности.

Измерение и понятие единиц измерения

Основная цель измерения состоит в том, чтобы получить информацию о величине, количестве или качестве измеряемого объекта или явления. Для этого необходимо использовать единицы измерения.

Единицы измерения — это установленные и принятые международными стандартами значения, которые используются для измерения различных физических величин. Единицы измерения обладают определенными свойствами, такими как взаимная сопоставимость и однозначность.

Единицы измерения могут быть различных типов, например, временные, длинные, массовые, объемные и т.д. Каждый тип величины имеет свои собственные единицы измерения. Например, для измерения длины используются единицы измерения, такие как метр, сантиметр, фут и т.д.

Единицы измерения имеют между собой отношения, которые могут быть линейными или нелинейными. Например, один метр равен 100 сантиметрам, что является примером линейного отношения. В то же время, отношение между массой и объемом является нелинейным.

Использование правильных единиц измерения является важным аспектом в науке и технике. Оно позволяет проводить точные измерения, сравнивать результаты и делать выводы на основе полученных данных. Поэтому важно понимать и использовать правильные единицы измерения в соответствии с измеряемыми величинами и задачами.

Вопрос-ответ:

Какие основные понятия изучает математика 3?

Математика 3 изучает такие основные понятия, как функции, производные, интегралы, множества, вероятность и статистика.

Зачем нужно изучать математику 3?

Изучение математики 3 позволяет получить глубокое понимание математических концепций и их применение в реальных ситуациях. Это полезно как для развития логического мышления, так и для решения сложных задач в различных областях науки и техники.

Какими методами можно решать задачи в математике 3?

В математике 3 можно использовать различные методы решения задач, включая аналитические, графические и численные методы. Аналитический метод основан на использовании формул и алгоритмов, графический метод использует построение графиков функций, а численный метод основан на приближенных вычислениях и использовании компьютерных программ.

Какие области науки и техники используют математику 3?

Математика 3 находит применение во многих областях науки и техники, таких как физика, химия, биология, экономика, информатика и многие другие. Например, в физике математика 3 используется для моделирования физических процессов, в экономике — для анализа рынков и оптимизации решений.

Видео по теме: