Математика 6 класс дроби как вычислять

Узнайте, как правильно вычислять дроби в математике для 6 класса. В этой статье вы найдете примеры и пошаговое объяснение для решения задач с дробями. Улучшите свои навыки работы с дробями и уверенно решайте задачи в школе.

Дроби – это математический объект, который используется для представления долей чисел. В шестом классе ученики начинают изучать основы работы с дробями, включая их вычисление.

Вычисление дробей – это процесс нахождения значения дроби или результата действий с дробями. Для этого необходимо знать основные правила работы с дробями и уметь применять их в практике.

Основные операции с дробями включают сложение, вычитание, умножение и деление. Для выполнения этих операций необходимо приводить дроби к общему знаменателю, а затем применять соответствующие правила.

Например, для сложения дробей с одинаковыми знаменателями необходимо просто сложить числители и оставить знаменатель без изменений. Если знаменатели разные, то необходимо привести дроби к общему знаменателю, сложить числители и результат записать с общим знаменателем. Это лишь одно из правил вычисления дробей, которые необходимо знать и применять для успешного решения задач.

Математика 6 класс: вычисление дробей

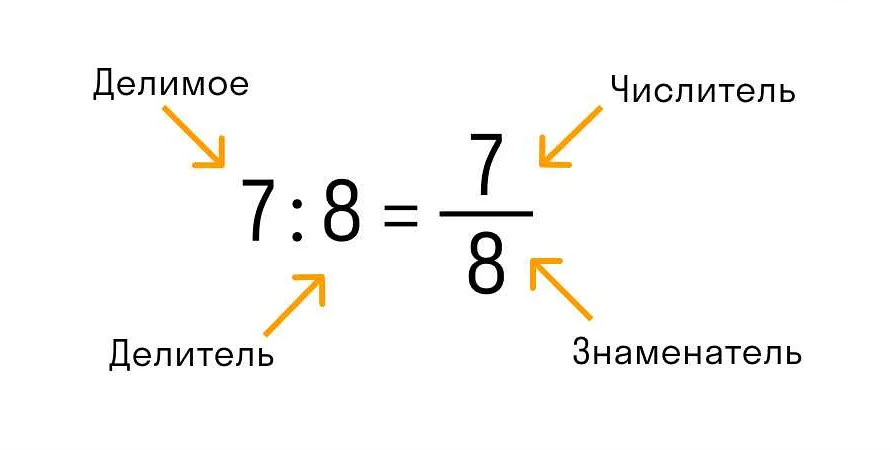
Для вычисления дробей мы используем основные арифметические операции: сложение, вычитание, умножение и деление. Например, чтобы сложить две дроби, нужно привести их к общему знаменателю, а затем сложить числители.

При вычитании дробей также приводим их к общему знаменателю, а затем вычитаем числители. При умножении дробей перемножаем числители и знаменатели, а при делении дробей умножаем делимую на обратную дробь делителя.

Также в 6 классе мы изучаем сравнение дробей. Для этого приводим дроби к общему знаменателю и сравниваем числители.

Для удобства вычислений и сравнений дробей используется таблица, в которой указываются числители, знаменатели и результаты операций. В таблице также можно использовать десятичные дроби для упрощения вычислений.

ЧислительЗнаменательСложениеВычитаниеУмножениеДеление

2	5	7/5	3/5	6/25	10/5
3	4	11/4	-1/4	6/16	12/4
1	2	5/2	1/2	3/4	2/2

Таким образом, в 6 классе мы изучаем основные операции с дробями и их вычисление при помощи таблицы. Эти навыки позволяют нам работать с числами, представленными в виде дробей, и использовать их в различных задачах и решениях.

Правила упрощения дробей

Вот некоторые правила упрощения дробей:

ПравилоПримерПояснение

1. Нахождение общего множителя числителя и знаменателя	\(\frac{4}{8}\)	Мы находим общий множитель числителя и знаменателя, в данном случае это число 4. Затем делим числитель и знаменатель на этот общий множитель и получаем упрощенную дробь \(\frac{1}{2}\).
2. Удаление общего множителя числителя и знаменателя	\(\frac{10}{15}\)	Если числитель и знаменатель имеют общий множитель, то мы можем упростить дробь, разделив оба числа на этот общий множитель. В данном случае общим множителем является число 5, поэтому упрощенная дробь будет \(\frac{2}{3}\).
3. Упрощение с помощью простых чисел	\(\frac{14}{21}\)	Если числитель и знаменатель имеют общие простые множители, то мы можем упростить дробь, разделив оба числа на эти общие множители. В данном случае общим простым множителем является число 7, поэтому упрощенная дробь будет \(\frac{2}{3}\).

Действия с дробями: сложение и вычитание

Сложение дробей производится следующим образом: сначала находим общий знаменатель, затем складываем числители и записываем результат в числитель дроби с общим знаменателем. Например, если нам даны дроби 2/3 и 1/4, то для их сложения нужно найти общий знаменатель, который будет равен 12 (наименьшее общее кратное чисел 3 и 4). Затем числители 2 и 1 складываем и получаем 3, а знаменатель оставляем неизменным (12). Итоговая дробь будет равна 3/12.

Вычитание дробей производится аналогичным образом, только мы вычитаем числители и записываем результат в числитель дроби с общим знаменателем. Например, если нам даны дроби 5/6 и 2/6, то для их вычитания нужно найти общий знаменатель, который будет равен 6. Затем числитель 5 вычитаем из числителя 2 и получаем 3. Знаменатель оставляем неизменным (6). Итоговая дробь будет равна 3/6.

Важно помнить, что перед сложением или вычитанием дробей необходимо привести их к общему знаменателю. Если дроби уже имеют общий знаменатель, то операции выполняются непосредственно с числителями.

В дальнейшем, при изучении математики, будут рассмотрены и другие действия с дробями, такие как умножение и деление. Однако сложение и вычитание являются основой для более сложных операций и являются неотъемлемой частью работы с дробями.

Умножение дробей

Например, чтобы умножить дроби 2/3 и 4/5, нужно выполнить следующие действия:

Числитель: 2 * 4 = 8

Знаменатель: 3 * 5 = 15

Итак, результат умножения дробей 2/3 и 4/5 равен 8/15.

Не забывайте сокращать полученные дроби, если это возможно. Для этого необходимо найти наибольший общий делитель числителя и знаменателя и поделить оба числа на него.

Умножение дробей может быть полезным при решении задач, связанных с долями, процентами и долями величин. Также оно используется в более сложных операциях с дробями, например, при делении дробей.

Деление дробей

Для деления дробей, нужно выполнить следующие шаги:

1. Умножить первую дробь (делимое) на обратную второй дробь (делитель).
2. Упростить полученную дробь, если это возможно.

Пример:

2 3

:

4 5

=

2 3

*

5 4

=

2 * 5 3 * 4

=

10 12

=

5 6

В данном примере, мы сначала умножили делимое 2/3 на обратную второй дроби 5/4, а затем упростили полученную дробь до несократимого вида.

Таким образом, деление дробей сводится к умножению первой дроби на обратную второй, а затем к упрощению полученной дроби.

Смешанные числа: перевод в дроби и обратно

Для перевода смешанного числа в дробь необходимо умножить целую часть на знаменатель дробной части и прибавить числитель дробной части. Получившуюся сумму записываем в числителе, а знаменатель остается тот же. Например, для числа 3 ½ мы умножаем 3 на 2 и прибавляем 1, получая дробь 7/2.

Обратно, чтобы перевести дробь в смешанное число, необходимо разделить числитель на знаменатель. Целая часть будет равна результату целочисленного деления, а остаток — дробной частью. Например, для дроби 7/2, мы делим 7 на 2 и получаем результат 3 с остатком 1. Таким образом, дробь 7/2 можно перевести в смешанное число 3 ½.

Перевод смешанных чисел в дроби и обратно позволяет удобно выполнять арифметические операции с такими числами. Зная эти правила, можно легко производить сложение, вычитание, умножение и деление смешанных чисел.

Вопрос-ответ:

Как складывать дроби с одинаковыми знаменателями?

Для сложения дробей с одинаковыми знаменателями нужно просто сложить их числители и записать получившуюся сумму над общим знаменателем. Например, если у нас есть дроби 3/5 и 2/5, то их сумма будет равна 5/5, что равно 1.

Как вычислять дроби с разными знаменателями?

Для вычисления дробей с разными знаменателями нужно привести их к общему знаменателю, а затем сложить их числители. Например, если у нас есть дроби 1/2 и 1/3, то можно привести их к общему знаменателю, который будет равен 6, и сложить числители: 3/6 + 2/6 = 5/6.

Как вычислить произведение двух дробей?

Для вычисления произведения двух дробей нужно перемножить их числители и знаменатели. Например, если у нас есть дроби 2/3 и 3/4, то их произведение будет равно (2 * 3) / (3 * 4) = 6/12, что можно упростить до 1/2.

Что делать, если в числителе дроби есть отрицательное число?

Если в числителе дроби есть отрицательное число, то знак «минус» ставится перед числителем, а знак «плюс» или «минус» перед знаменателем остается без изменений. Например, если у нас есть дробь -2/5, то она остается без изменений.

Как вычислить частное двух дробей?

Для вычисления частного двух дробей нужно умножить первую дробь на обратную второй. Обратная дробь получается путем поменяния местами числителя и знаменателя. Например, если у нас есть дроби 2/3 и 3/4, то их частное будет равно (2/3) * (4/3) = (2 * 4) / (3 * 3) = 8/9.

Как вычислить сумму дробей с одинаковыми знаменателями?

Сумма дробей с одинаковыми знаменателями вычисляется путем сложения числителей и оставления знаменателя неизменным. Например, чтобы найти сумму дробей 1/4 и 3/4, нужно сложить числители: 1 + 3 = 4, и знаменатель оставить без изменений: 4/4. Итак, сумма этих двух дробей равна 4/4, что равно 1.

Как вычислить разность дробей с разными знаменателями?

Разность дробей с разными знаменателями вычисляется путем перевода дробей к общему знаменателю и вычитания числителей. Например, чтобы найти разность дробей 3/5 и 1/3, нужно найти общий знаменатель, который равен 15. Затем дроби переводятся к общему знаменателю, умножая числитель и знаменатель каждой дроби на необходимый коэффициент. В данном случае первая дробь станет 9/15, а вторая дробь станет 5/15. Итак, разность этих двух дробей равна 9/15 — 5/15 = 4/15.

Примеры решения задач по дробям

Чтобы проиллюстрировать как вычислять дроби, рассмотрим несколько примеров:

1. 1. Задача: Вычислить сумму дробей 1/3 и 2/5.

Решение: Для сложения дробей необходимо привести их к общему знаменателю. Найдем наименьшее общее кратное (НОК) знаменателей 3 и 5, которым является число 15. Теперь приведем дроби к общему знаменателю:

1. 1. • 1/3 = 5/15 (умножаем числитель и знаменатель первой дроби на 5)
      • 2/5 = 6/15 (умножаем числитель и знаменатель второй дроби на 3)

Теперь складываем числители дробей:

5/15 + 6/15 = 11/15

Ответ: Сумма дробей 1/3 и 2/5 равна 11/15.

1. 1. Задача: Вычислить разность дробей 3/4 и 1/2.

Решение: Для вычитания дробей также необходимо привести их к общему знаменателю. Найдем НОК знаменателей 4 и 2, которым является число 4. Приведем дроби к общему знаменателю:

1. 1. • 3/4 = 3/4 (числитель и знаменатель первой дроби остаются без изменений)
      • 1/2 = 2/4 (умножаем числитель и знаменатель второй дроби на 2)

Теперь вычитаем числители дробей:

3/4 — 2/4 = 1/4

Ответ: Разность дробей 3/4 и 1/2 равна 1/4.

1. 1. Задача: Вычислить произведение дробей 2/3 и 4/5.

Решение: Для умножения дробей перемножим числители и знаменатели:

2/3 * 4/5 = 8/15

Ответ: Произведение дробей 2/3 и 4/5 равно 8/15.

1. 1. Задача: Вычислить частное дробей 3/5 и 1/4.

Решение: Для деления дробей умножим первую дробь на обратное значение второй дроби:

3/5 ÷ 1/4 = 3/5 * 4/1 = 12/5

Ответ: Частное дробей 3/5 и 1/4 равно 12/5.

Видео по теме: