Математика 6 класс мерзляк 336 как делать

Делайте математику в 6 классе по учебнику Мерзляка 336 страница эффективно и правильно. Научитесь решать задачи, выполнять упражнения и разбираться с темами учебника. Получите полезные советы и стратегии для успешного изучения математики.

Учебник Мерзляка по математике для 6 класса является одним из самых популярных учебников в школах России. В нем содержатся разнообразные задания, которые помогут школьникам развивать навыки решения математических задач и понимание основных концепций.

Однако, не всегда ученикам удается успешно справиться с заданиями, представленными в этом учебнике. Для того чтобы правильно делать задания, необходимо следовать определенным правилам и стратегиям.

Во-первых, перед началом решения задачи необходимо внимательно прочитать ее условие и выделить ключевые моменты. Затем следует определить, какие известные данные даны в задаче, и что именно требуется найти. Это поможет структурировать задачу и понять, какой подход следует выбрать для ее решения.

Во-вторых, необходимо использовать известные математические формулы и принципы для решения задачи. Если задача не является стандартной, можно попробовать применить различные методы и подходы к ее решению. Важно помнить, что математика – это не только решение задач, но и развитие логического мышления и творческих способностей.

Наконец, после решения задачи стоит проверить полученный ответ и убедиться, что он соответствует условию задачи. Если ответ неверный, необходимо проанализировать свои ошибки и найти правильное решение. Это поможет улучшить навыки решения задач и повысить успех в изучении математики.

Таким образом, для успешного выполнения заданий по математике из учебника Мерзляка 6 класса необходимо внимательно читать условие задачи, использовать математические знания и методы решения, а также проверять полученный ответ на соответствие условию задачи. Не бойтесь экспериментировать и применять различные подходы к решению задач – это поможет вам развивать свои математические способности и достигать успеха в изучении этого предмета.

Основные понятия математики

Основные понятия математики включают в себя:

Числа: числа используются для измерения количества, они могут быть натуральными, целыми, рациональными или иррациональными. Числа могут быть положительными, отрицательными или нулем.

Операции: операции — это математические действия, такие как сложение, вычитание, умножение и деление. Они используются для решения задач и получения результатов.

Формулы: формулы — это математические выражения, которые описывают взаимосвязь между различными величинами. Формулы часто используются для решения задач и нахождения неизвестных значений.

Геометрия: геометрия — это раздел математики, который изучает фигуры, их свойства и взаимное расположение. Геометрические фигуры могут быть двухмерными (плоскостью) или трехмерными (пространством).

Вероятность: вероятность — это раздел математики, который изучает случайные явления и их вероятность возникновения. Вероятность используется для прогнозирования результатов различных событий.

Статистика: статистика — это раздел математики, который изучает сбор, анализ и интерпретацию данных. Статистика помогает делать выводы и прогнозы на основе доступной информации.

Основные понятия математики являются основой для более сложных математических концепций и применяются в повседневной жизни.

Работа с уравнениями

Для решения уравнения нужно найти значение переменной, которое удовлетворяет условию уравнения. Существует несколько способов решения уравнений, но основной метод, который вы будете использовать, называется приведение подобных членов.

Приведение подобных членов — это процесс, при котором слагаемые с одинаковыми переменными и степенями собираются вместе. Например, если у вас есть уравнение 2х + 3х = 10, вы можете сложить слагаемые с переменной x: 2х + 3х = 5х. Теперь у вас есть уравнение 5х = 10.

Далее нужно избавиться от коэффициента при переменной, чтобы оставить только саму переменную. В нашем случае, чтобы избавиться от коэффициента 5, нужно поделить обе части уравнения на 5: (5х) / 5 = 10 / 5. Это даст вам уравнение х = 2.

Проверьте, подставив найденное значение переменной в исходное уравнение: 2х + 3х = 10. 2 * 2 + 3 * 2 = 4 + 6 = 10. Уравнение верное, значит, ваше решение правильно.

Помните, что при решении уравнений важно следить за знаками и выполнить все необходимые действия по приведению подобных членов. Также не забывайте проверять полученное решение, чтобы убедиться в его правильности.

Уравнения являются важным инструментом в математике и используются во многих областях науки и техники. Понимание основ работы с уравнениями поможет вам справляться с более сложными задачами и развивать свои математические навыки.

Работа с графиками

Для правильной работы с графиками необходимо уметь анализировать и интерпретировать информацию на графике. Важно понимать основные элементы графика, такие как оси координат, точки, отрезки и кривые.

Прежде чем начать работу с графиками, необходимо освоить некоторые базовые понятия и навыки, такие как построение координатной плоскости, определение значений функции для заданных значений аргумента, нахождение точек пересечения графиков и т.д.

Для успешного выполнения заданий по работе с графиками важно уметь анализировать и интерпретировать информацию на графиках, а также применять полученные знания для решения задач. Необходимо уметь определять значения функции для заданных значений аргумента, находить точки пересечения графиков, а также проводить прямые и кривые линии на графике.

При выполнении заданий по работе с графиками важно быть внимательным и точным, чтобы избежать ошибок. Необходимо тщательно анализировать информацию на графике, использовать правильные формулы и методы для решения задач, а также проверять полученные ответы на правильность.

Работа с графиками не только развивает навыки в области математики, но и помогает развить логическое мышление, аналитические способности и умение применять математические знания на практике.

Сложение и вычитание дробей

В математике существуют различные операции с дробями, включая сложение и вычитание. Чтобы правильно выполнять эти операции, необходимо понимать основные правила и принципы.

При сложении и вычитании дробей важно учитывать их общий знаменатель. Если дроби имеют одинаковый знаменатель, сложение и вычитание сводятся к операции с числителями. В этом случае достаточно просто прибавить или вычесть числители и записать результат с общим знаменателем.

Если дроби имеют разные знаменатели, необходимо привести их к общему знаменателю. Для этого находится наименьшее общее кратное знаменателей и каждую дробь приводят к этому знаменателю, умножая и числитель, и знаменатель на одно и то же число.

После приведения дробей к общему знаменателю можно выполнить сложение или вычитание, как в случае с одинаковыми знаменателями. Результат также записывается с общим знаменателем.

Важно помнить, что при выполнении операций со сложением и вычитанием дробей необходимо сокращать полученную дробь, если это возможно. Для этого находится наибольший общий делитель числителя и знаменателя и дробь сокращается на этот делитель.

Правильное выполнение сложения и вычитания дробей требует тщательного и последовательного выполнения каждого шага. Важно не пропустить ни одной операции и проверить правильность полученного результата.

Повторение и практика помогут улучшить навыки работы с дробями и выполнение операций сложения и вычитания. Чем больше задач решено, тем лучше понимание и навыки будут приобретены.

Сложение и вычитание дробей – это важный раздел математики, который стоит уделить должное внимание и время для освоения. Систематическое изучение материала и множество практических задач помогут достичь успеха и уверенности в решении подобных заданий.

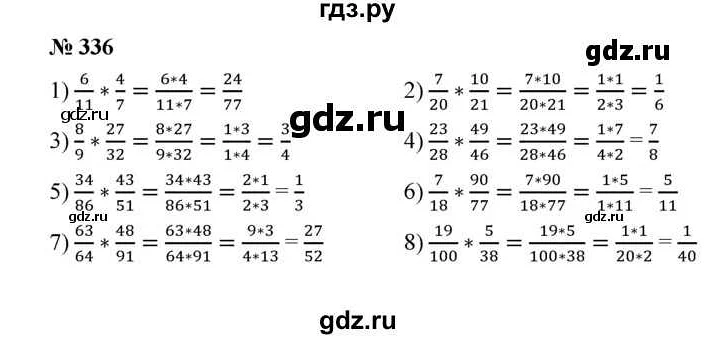
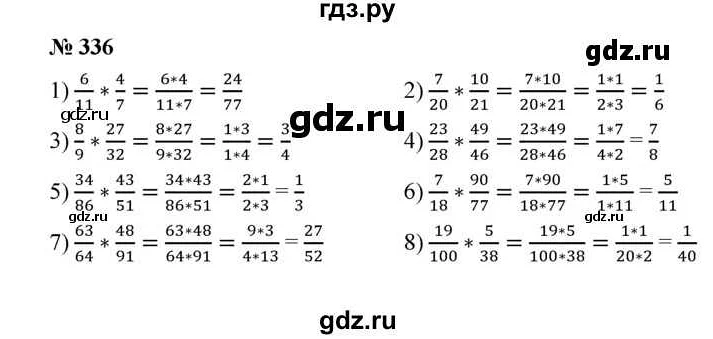
Умножение и деление дробей

Умножение двух дробей производится следующим образом: умножаем числитель первой дроби на числитель второй дроби и получаем числитель результата. Затем умножаем знаменатель первой дроби на знаменатель второй дроби и получаем знаменатель результата. Таким образом, результатом умножения двух дробей является дробь, у которой числитель равен произведению числителей и знаменатель равен произведению знаменателей.

Деление двух дробей производится следующим образом: умножаем числитель первой дроби на знаменатель второй дроби и получаем числитель результата. Затем умножаем знаменатель первой дроби на числитель второй дроби и получаем знаменатель результата. Таким образом, результатом деления двух дробей является дробь, у которой числитель равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель равен произведению знаменателя первой дроби на числитель второй дроби.

Для выполнения умножения и деления дробей рекомендуется использовать таблицу, чтобы наглядно представить процесс.

Умножение дробейДеление дробей

a c b d

a c b d

Результат умножения двух дробей a/b и c/d будет равен a*c/b*d.

Результат деления двух дробей a/b и c/d будет равен a*c/b*d.

Таким образом, для выполнения умножения и деления дробей необходимо умножить числители и знаменатели, соответственно, и записать результат в виде дроби с упрощенными числителем и знаменателем, если это возможно.

Проценты и доли

Процент – это сотая часть числа. Обозначается знаком % и применяется для выражения отношения одной величины к другой. Проценты часто используются для обозначения доли, долей величины или изменения.

Доля – это отношение одной величины к другой, выраженное в виде десятичной или обыкновенной дроби. Доля может быть меньше, равна или больше 1.

Для работы с процентами и долями необходимо уметь выполнять следующие операции:

1. Находить процент от числа
2. Находить число, если процент от него известен
3. Находить долю величины
4. Находить величину, если доля известна
5. Выполнять преобразование процентов в десятичные и обыкновенные дроби, и наоборот

Для решения задач по процентам и долям необходимо использовать соответствующие формулы и методы решения, а также быть внимательным и аккуратным при выполнении вычислений. Ошибки в расчетах могут привести к неверным результатам и неправильному решению задачи.

При решении задач по процентам и долям полезно использовать логическое мышление, анализировать условие задачи, строить схему решения и проверять полученные результаты. Также важно уметь переводить проценты в доли и наоборот, а также проводить преобразования между десятичными и обыкновенными дробями.

Важно знать, что проценты и доли имеют широкое применение в реальной жизни и находятся повсюду в нашем окружении. Поэтому умение работать с процентами и долями является необходимым навыком для успешного решения задач и принятия рациональных решений в различных ситуациях.

Геометрические фигуры и их свойства

Одной из основных геометрических фигур является треугольник. Треугольник состоит из трех сторон и трех углов. У треугольника есть несколько свойств, например:

• Сумма углов треугольника: сумма всех углов треугольника равна 180 градусам.
• Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Окружность — это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. У окружности также есть свои свойства:

• Диаметр: отрезок, соединяющий две точки на окружности и проходящий через центр.
• Радиус: отрезок, соединяющий центр окружности с любой точкой на окружности.
• Длина окружности: произведение диаметра на число Пи.

Круг — геометрическое тело, образованное вращением окружности вокруг ее диаметра.

Это лишь некоторые из множества геометрических фигур, каждая из которых имеет свои уникальные свойства. Изучение геометрии позволяет узнать их и легко применять для решения задач.

Подведение итогов

При проверке заданий обратите внимание на следующие аспекты:

Правильность ответов: проверьте, что вы правильно решали задачи и что ответы соответствуют требованиям задания. Убедитесь, что ответы представлены в правильной форме и с правильными единицами измерения.

Понимание материала: задания должны помочь вам укрепить и углубить свои знания в математике. Убедитесь, что вы понимаете принципы и методы решения задач, а не просто механически повторяете действия.

Точность и аккуратность: важно, чтобы ваши решения были аккуратными и точными. Проверьте свои вычисления на ошибки, такие как опечатки, неверное копирование чисел или неправильная расстановка знаков.

Самостоятельность: задания следует выполнять самостоятельно, без помощи дополнительных материалов или других людей. Это поможет вам развить навык самостоятельного мышления и решения проблем.

Важно помнить, что математика – это предмет, требующий постоянной практики и усилий. Регулярное выполнение заданий поможет вам улучшить свои навыки и достичь успеха в изучении математики.

Успехов в дальнейшем изучении математики!

Вопрос-ответ:

Как правильно решить задание по математике в 6 классе?

Для правильного решения задания по математике в 6 классе нужно внимательно прочитать условие, выделить ключевые данные и использовать соответствующие математические формулы и методы решения. Также важно следовать логике решения, делать необходимые вычисления и проверять полученный ответ.

Какой подход использовать для выполнения заданий по математике в 6 классе?

Для выполнения заданий по математике в 6 классе рекомендуется использовать систематический подход. Сначала прочитайте задание и попробуйте понять, что от вас требуется. Затем разберите задачу на более мелкие части и определите, какие формулы и методы нужно использовать для ее решения. После этого выполняйте необходимые вычисления и проверьте полученный ответ на логическую и математическую правильность.

Какие ошибки чаще всего допускаются при решении задач по математике в 6 классе?

При решении задач по математике в 6 классе часто допускаются следующие ошибки: неправильное понимание условия задачи, неправильное применение математических формул и методов, неправильные вычисления, неправильный ответ. Также некоторые ученики могут не следовать логике решения задачи или упускать важные детали.

Какие советы можно дать по выполнению заданий по математике в 6 классе?

Для успешного выполнения заданий по математике в 6 классе можно использовать следующие советы: внимательно прочитывайте условие задачи и выделяйте ключевые данные, разбивайте задачу на более простые части, используйте соответствующие математические формулы и методы, делайте необходимые вычисления и проверяйте полученный ответ на логическую и математическую правильность. Также полезно тренироваться на разнообразных заданиях и просить помощи у учителя или одноклассников, если что-то непонятно.

Видео по теме: