Что такое математика для детей 4 класса

Математика для детей 4 класса – это предмет, который помогает развивать логическое мышление и навыки решения простых математических задач. Ученики учатся считать, складывать, вычитать и умножать числа, а также изучают геометрию и измерение. Изучение математики в 4 классе помогает детям развивать навыки анализа, решения проблем и критического мышления, которые будут полезны в будущем. Это также способствует развитию самодисциплины и уверенности в себе у детей.

Математика — это один из самых важных предметов в школе, который помогает развивать логическое мышление и умение решать задачи. В 4 классе ученики начинают изучать основные понятия и задачи этой науки, которые будут полезны им не только в школе, но и в повседневной жизни.

Одним из основных понятий, которые изучают в 4 классе, является число. Ученики узнают, как записывать числа, как сравнивать их, а также учатся складывать, вычитать, умножать и делить числа. Они также знакомятся с понятием десятичной системы счисления и научаются работать с числами до 10000.

В 4 классе дети также изучают геометрию. Они узнают, что такое точка, линия, отрезок, угол и фигура. Дети учатся строить и измерять отрезки, находить середину отрезка и строить перпендикулярные прямые. Они также знакомятся с разными фигурами, такими как треугольник, квадрат, прямоугольник и круг, и учатся определять их свойства.

Математика для детей 4 класса не только помогает им развивать математическое мышление, но и учит решать задачи. Дети учатся формулировать задачу, находить ее решение и проверять его правильность. Они также изучают разные виды задач, такие как задачи на сложение, вычитание, умножение и деление, а также задачи на логику и рассуждение. Все это помогает развивать у детей навыки анализа, решения проблем и принятия решений.

Изучение математики в 4 классе является важным этапом в развитии учеников. Они получают базовые знания, которые помогут им в дальнейшем обучении и повседневной жизни. Поэтому важно, чтобы дети с интересом и усердием изучали этот предмет, задавали вопросы и применяли полученные знания на практике.

Арифметика: основы

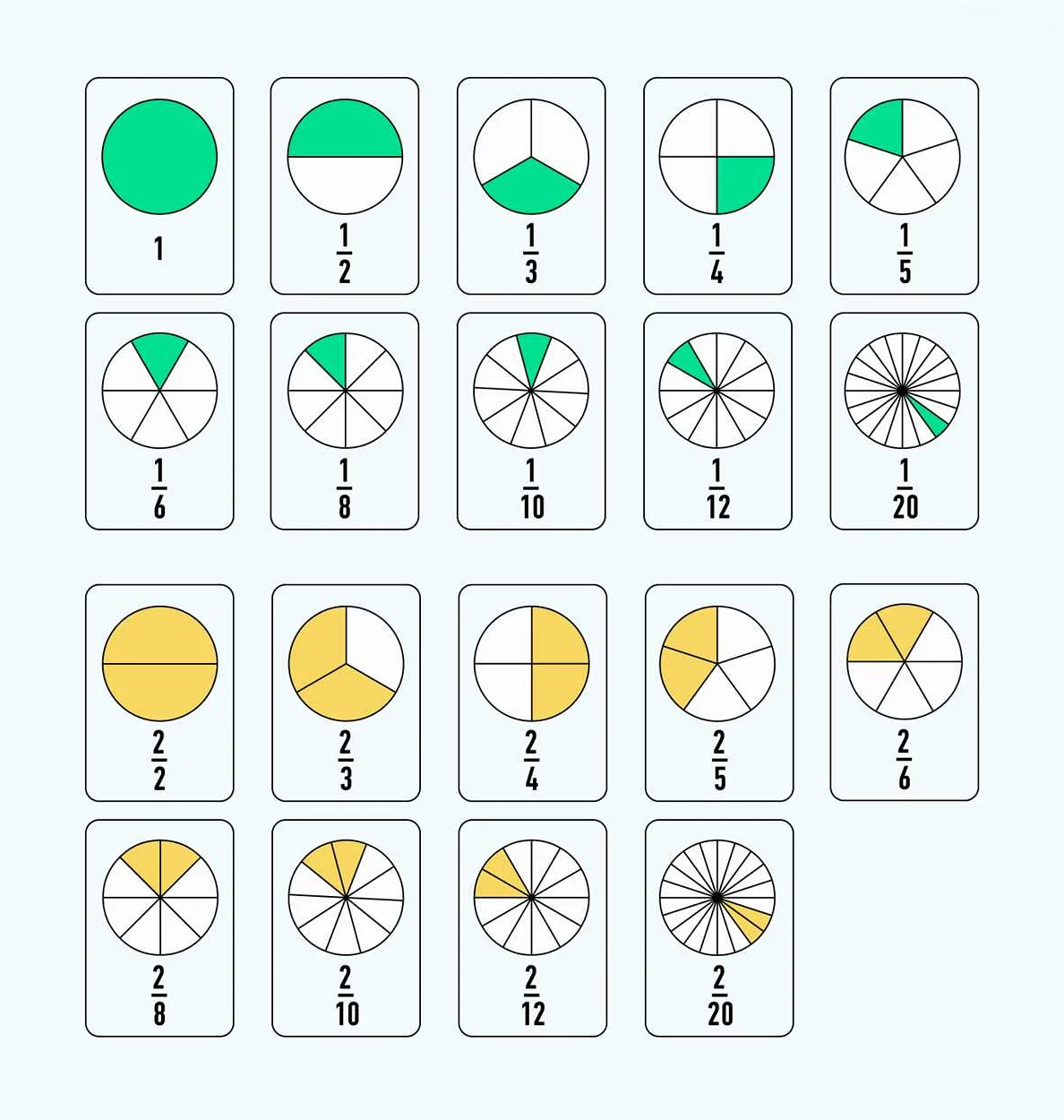
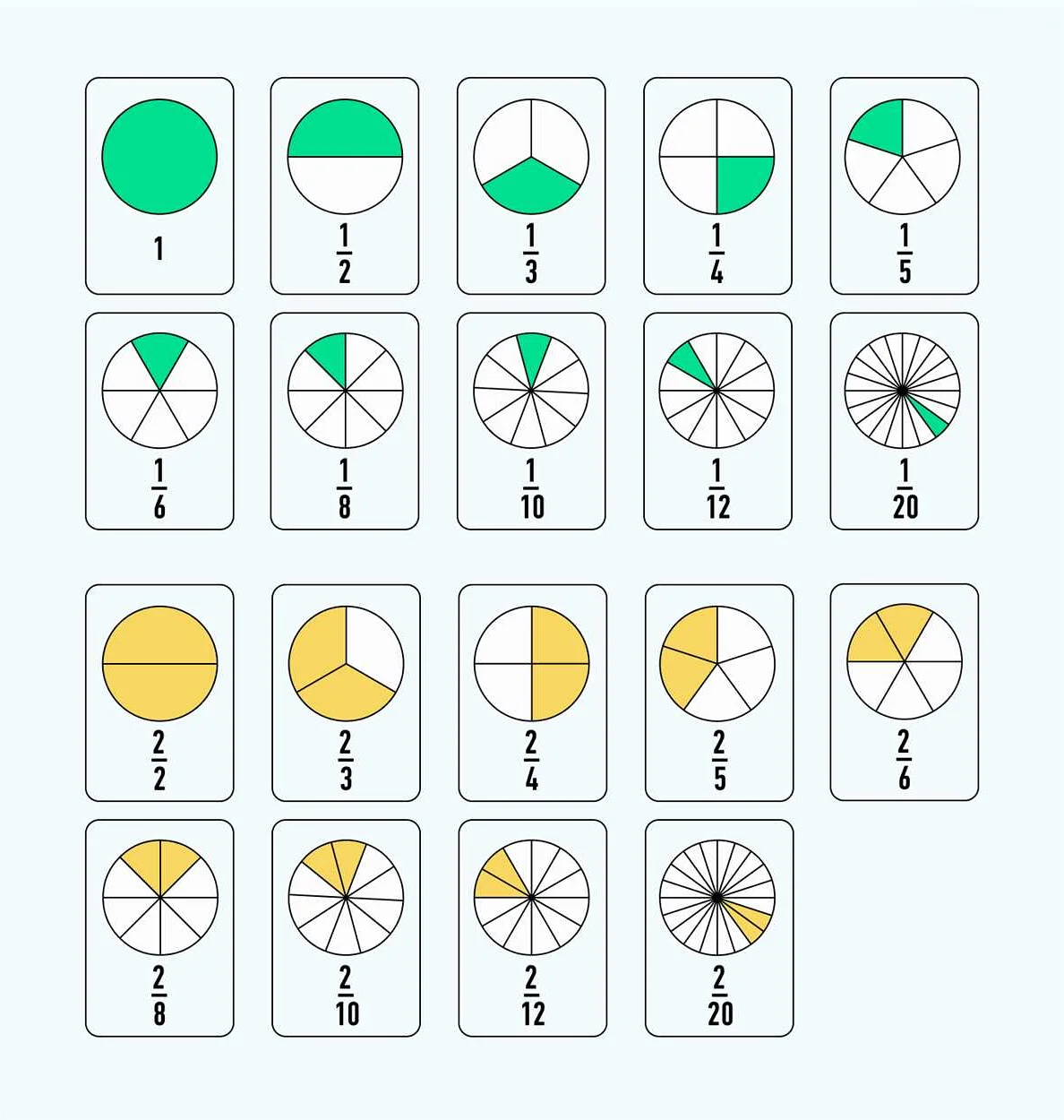
В арифметике используются различные термины и понятия:

• Числа — это основные элементы арифметики. Они могут быть натуральными, целыми, рациональными или иррациональными.
• Сложение — это операция, которая позволяет складывать два или более числа и получать их сумму.
• Вычитание — это операция, которая позволяет вычитать одно число из другого и получать разность.
• Умножение — это операция, которая позволяет умножать два или более числа и получать их произведение.
• Деление — это операция, которая позволяет делить одно число на другое и получать частное.
• Знаки операций — плюс (+) используется для обозначения сложения, минус (-) — для обозначения вычитания, умножения — знак «×» или «*», а деления — знак «/» или «÷».

Основные правила арифметики:

1. При выполнении операций нужно сначала выполнять умножение и деление, а затем сложение и вычитание.
2. Приоритет операций можно изменять с помощью скобок.
3. При сложении и умножении можно изменять порядок чисел, результат будет одинаковым.
4. При вычитании и делении порядок чисел важен, результат будет разным.

Знание арифметики помогает решать различные задачи, как в повседневной жизни, так и в математике.

Видео по теме:

Геометрия: фигуры и их свойства

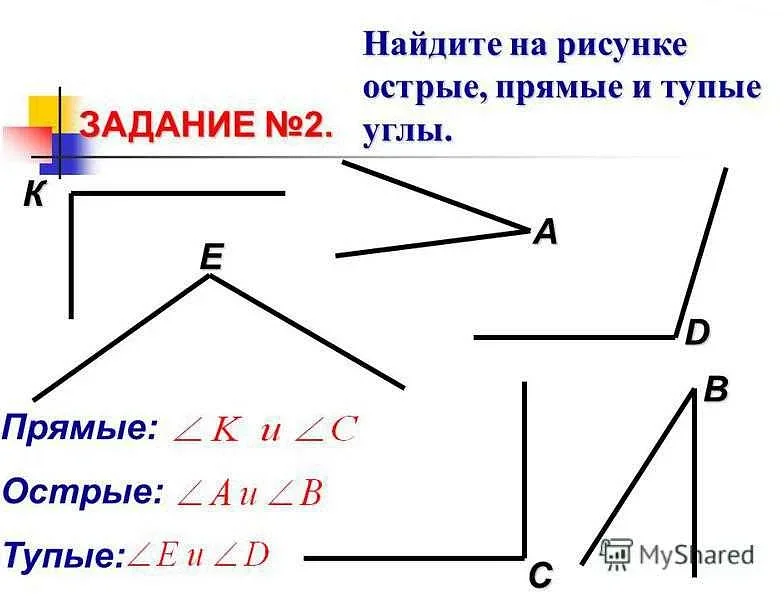
Основные понятия геометрии включают в себя фигуры, линии, углы, точки, периметр и площадь.

Фигуры — это геометрические объекты, имеющие определенную форму. Среди фигур можно выделить такие базовые типы как круг, квадрат, прямоугольник, треугольник. Каждая из этих фигур имеет свои уникальные свойства и характеристики.

Линии — это геометрические объекты, состоящие из бесконечного числа точек, которые расположены в одном направлении. Примерами линий могут быть прямая, отрезок, луч.

Углы — это области в плоскости между двумя линиями, которые сходятся в одной точке. Углы бывают острые, прямые, тупые и разносторонние.

Точки — это основные элементы геометрии, которые не имеют размера и обозначаются буквами. Точки применяются для указания местоположения фигур и проведения линий.

Периметр — это сумма длин всех сторон фигуры. Периметр помогает определить, насколько длинная граница у фигуры.

Площадь — это количество площади, занимаемой фигурой в плоскости. Площадь позволяет оценить, сколько пространства занимает фигура.

Изучение геометрии помогает детям развивать пространственное мышление, логику и абстрактное мышление. Оно также помогает решать задачи, связанные с измерением и конструированием.

Важно: Правильное понимание геометрии и ее применение помогут ребенку лучше понимать окружающий мир и успешно решать математические задачи.

Измерение: длина, масса, объем

Одним из важных аспектов измерения является измерение длины. Длина – это расстояние между двумя точками. Для измерения длины используются различные единицы измерения, такие как метры, сантиметры и миллиметры. Например, длина стола может быть измерена в метрах, а длина ручки – в сантиметрах.

Кроме длины, в математике также измеряют массу. Масса – это количество вещества в теле или предмете. Для измерения массы используются единицы, такие как килограммы, граммы и тонны. Например, масса человека может быть измерена в килограммах, а масса яблоки – в граммах.

Еще одним важным аспектом измерения является измерение объема. Объем – это количество пространства, занимаемого телом или предметом. Для измерения объема используются единицы, такие как кубические метры, литры и миллилитры. Например, объем аквариума может быть измерен в литрах, а объем воды в стакане – в миллилитрах.

Измерение длины, массы и объема позволяет нам делать точные оценки и сравнивать различные объекты и явления. Понимание этих понятий и умение работать с ними не только помогает в решении математических задач, но и в повседневной жизни.

Вопрос-ответ:

Какие понятия изучают в математике в 4 классе?

В математике 4 класса изучаются такие понятия, как числа и операции, геометрические фигуры, измерение, таблица умножения, решение задач на пропорциональность и примеры с двумя неизвестными.

Какие задачи можно решать в математике в 4 классе?

В математике 4 класса можно решать задачи на сложение, вычитание, умножение и деление, задачи на нахождение периметра и площади прямоугольников и квадратов, задачи на нахождение площади и периметра треугольников и задачи на нахождение неизвестных чисел.

Какие операции с числами нужно знать в 4 классе?

В 4 классе нужно знать операции сложения, вычитания, умножения и деления. Также нужно уметь складывать и вычитать десятки и сотни, умножать и делить на однозначные числа и решать примеры с двумя действиями.

Какие геометрические фигуры изучают в математике в 4 классе?

В математике 4 класса изучаются такие геометрические фигуры, как прямоугольник, квадрат, треугольник, круг и многоугольник. Дети учатся определять их свойства, находить периметр и площадь, а также строить их по заданным параметрам.

Какие навыки развиваются при изучении математики в 4 классе?

При изучении математики в 4 классе развиваются навыки работы с числами, операциями, таблицей умножения, геометрическими фигурами и решением задач. Дети учатся анализировать и решать математические задачи, логически мыслить, применять математические знания на практике.

Какие основные понятия изучают в математике в 4 классе?

В четвертом классе дети изучают основные понятия математики, такие как натуральные числа, десятичная система счисления, арифметические действия (сложение, вычитание, умножение и деление), решение простых уравнений и задач на их основе, геометрические фигуры и их свойства, а также начальные представления о вероятности и статистике.

Графики: построение и анализ

Построение графиков – один из основных навыков, которым должен овладеть каждый ученик. Для построения графика функции необходимо знать ее уравнение и выбрать набор значений аргумента. Затем эти значения подставляются в уравнение, и для каждого значения аргумента находится соответствующее значение функции. Полученные точки можно отметить на координатной плоскости и соединить их линией, получив таким образом график функции.

Анализ графиков позволяет выявить различные характеристики функции. Например, по графику можно определить, является ли функция возрастающей или убывающей на заданном интервале. Также по графику можно определить точки, в которых функция достигает максимальных и минимальных значений – экстремумов. График также позволяет определить периодичность функции, наличие асимптот и другие характеристики.

Изучение графиков функций позволяет развить важные навыки анализа данных, логического мышления и решения задач. Построение и анализ графиков являются неотъемлемой частью математического образования и могут быть использованы в решении различных задач в реальной жизни.

Дроби: основные понятия и операции

Например, в дроби 3/4, числитель равен 3, а знаменатель равен 4. Это означает, что мы рассматриваем 3 части целого числа и разбиваем его на 4 равные части.

Операции с дробями включают сложение, вычитание, умножение и деление. Чтобы выполнить эти операции, мы должны привести дроби к общему знаменателю.

Например, для сложения дробей 1/2 и 1/3, мы должны привести их к общему знаменателю, который равен 6. После этого мы складываем числители и оставляем знаменатель неизменным, получая результат 5/6.

Также можно выполнять операции смешанных чисел, которые состоят из целой части и дробной части. Например, смешанное число 2 1/4 означает, что у нас есть 2 целые части и 1/4 часть.

Важно понимать, что дроби являются неотъемлемой частью математики и используются в различных сферах жизни, таких как рецепты, финансы и многое другое.

В заключение, знание основных понятий и операций с дробями позволяет решать различные задачи и упрощает понимание математики в целом.

Пропорции и проценты: простые задачи

Пропорция – это равенство двух отношений. Например, если 3 яблока стоят 150 рублей, то сколько стоят 5 яблок? Для решения такой задачи нужно составить пропорцию: 3/150 = 5/х, где х – неизвестное значение. Путем простых вычислений можно найти значение х.

Процент – это способ представления доли от целого в виде сотых долей. Например, если ребенок правильно решил 8 задач из 10, то его результат можно выразить в процентах: 8/10 * 100% = 80%. Таким образом, ребенок правильно решил 80% задач.

Важно научить ребенка применять пропорции и проценты в реальных ситуациях. Например, если в магазине проходит акция, где товар снижен на 20%, то сколько стоит товар после скидки? Для решения этой задачи нужно вычислить 20% от цены товара и вычесть это значение из исходной цены.

Еще одна полезная задача связана с распределением денежных средств. Например, если родители выделили ребенку 1000 рублей, а он хочет потратить 30% на игрушки и 40% на книги, то сколько денег останется у ребенка? Для решения этой задачи нужно вычислить 30% и 40% от суммы и вычесть эти значения из 1000 рублей.

Задачи на пропорции и проценты помогут развить логическое мышление и математические навыки у ребенка. Постепенно увеличивайте сложность задач и убедитесь, что ребенок понимает основные понятия и умеет применять их на практике.

Решение уравнений: базовые методы

Существует несколько базовых методов решения уравнений. Одним из самых простых методов является метод подстановки. При использовании этого метода необходимо подставить различные значения вместо неизвестной величины и проверить, выполняется ли равенство в уравнении.

Еще одним методом решения уравнений является метод равенства нулю. Для его применения необходимо преобразовать уравнение таким образом, чтобы все элементы были на одной стороне, а на другой стороне остался ноль. Затем необходимо проанализировать полученное уравнение и найти значения неизвестной величины, при которых оно будет выполняться.

Также для решения уравнений можно использовать методы противоположности и сокращения. Метод противоположности заключается в замене неизвестной величины на ее противоположную. Метод сокращения позволяет преобразовать уравнение таким образом, чтобы сократить его сложность и упростить процесс решения.

Обучение базовым методам решения уравнений позволяет детям развить логическое мышление и умение анализировать математические задачи. Эти навыки будут полезными не только в школьной программе, но и в повседневной жизни, где математика играет важную роль.

Задачи на логику и рассуждение

Задачи на логику и рассуждение помогают развивать мышление и логическое мышление у детей. Эти задачи требуют от учеников анализировать информацию, делать выводы, решать проблемы и находить рациональные решения.

Пример задачи на логику: В классе было 25 учеников. 15 из них любят футбол, 10 – хоккей, 5 – и футбол, и хоккей. Сколько учеников не интересуются ни футболом, ни хоккеем?

Чтобы решить эту задачу, нужно использовать логическое мышление и рассуждать: если в классе 15 учеников любят футбол, а 5 из них любят и футбол, и хоккей, то 10 учеников любят только футбол. Аналогично, если 10 учеников любят хоккей, а 5 из них любят и футбол, и хоккей, то 5 учеников любят только хоккей. Итак, 10 + 5 = 15 учеников интересуются футболом или хоккеем. Значит, 25 — 15 = 10 учеников не интересуются ни футболом, ни хоккеем.

Вы можете использовать подобные задачи для тренировки логического мышления у детей. Они не только помогут им развить навыки рассуждения, но и сделают процесс изучения математики более интересным и увлекательным.