Математика в науках естествознания: ее роль и значение

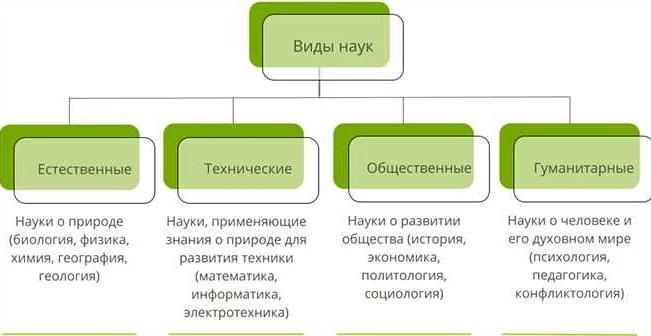
Математика является одним из основных естественных наук, которая изучает законы и свойства количественных отношений и форм, лежащих в основе природы и общества.

Математика является одним из фундаментальных предметов естественных наук, которые изучают общие законы и закономерности природы. Она является наукой об отношениях и структурах, дает нам возможность описывать явления и процессы, которые невозможно описать естественным языком.

Математика имеет тесную связь с другими естественными науками, так как она используется для моделирования и описания различных явлений в физике, химии, биологии и других научных дисциплинах. Без математических методов и понятий изучение природы было бы гораздо сложнее и менее точным.

Но не только природа подчиняется математическим законам, но и сама математика является частью природы. Например, геометрия изначально возникла из изучения пространственных форм и размеров в природе. А теория вероятностей была разработана для анализа случайных явлений в жизни. Таким образом, математика и природа неразрывно связаны, и каждый новый открытый закон природы заставляет нас пересматривать и расширять наши математические понимания.

Математика как естественная наука

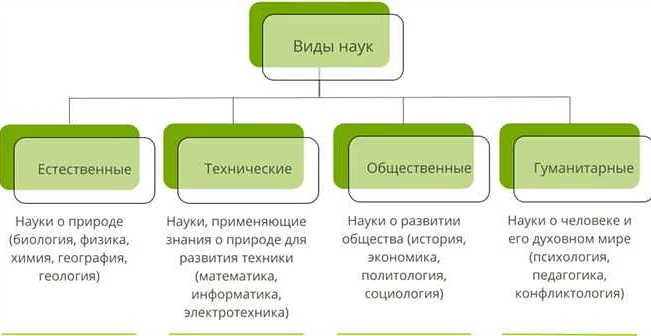
Многие склонны считать математику чем-то абстрактным и не имеющим отношения к реальному миру. Однако на самом деле, математика является одной из основных естественных наук.

Математика позволяет выражать законы природы в числах и формулах, создавая точные модели и прогнозы. Для решения реальных задач, таких как прогноз погоды или проектирование новых технологий, математика является неотъемлемой частью исследований.

Кроме того, математика играет ключевую роль в других естественных науках, таких как физика, химия, биология и т.д. Без математических методов и инструментов невозможно проводить точные измерения и эксперименты, а также анализировать полученные результаты.

Таким образом, математика является необходимым инструментом для изучения и понимания природы. Её развитие активно взаимодействует с другими естественными науками, помогая нам лучше понимать мир вокруг нас и создавать новые технологии для улучшения жизни на планете.

Ее наслоение на физику, химию и биологию

Математика тесно связана с естественными науками, такими как физика, химия и биология. Изучение данных дисциплин требует от ученых высокой математической подготовки и использования математических методов и моделей. Без математики физика, химия и биология не могут решать сложные задачи и предсказывать будущие события и явления в природе.

Физика и математика взаимно связаны друг с другом, существуют законы физики, которые могут быть описаны при помощи математических уравнений. Без математики мы бы не смогли описывать движение тел и расчет энергии в физических системах.

Химия также тесно связана с математикой. Химики используют математические методы для проведения сложных расчетов, таких как определение приближенных значений энергии, распределения электронов и т.д. Без математики мы не смогли бы описывать химические реакции и исследовать свойства веществ.

В биологии, математика помогает в моделировании сложных биологических систем, таких как популяционная динамика, метаболизм и генетика. Математические методы позволяют ученым прогнозировать биологические эксперименты и устанавливать закономерности в природе.

Таким образом, математика играет важную роль в естественных науках и представляет собой ключевой инструмент для понимания и исследования природы.

Роль математики в современной науке и технологиях

Математика играет огромную роль в современной науке и технологиях. Без ее использования невозможно представить современный мир, в котором мы живем. Математика является необходимым инструментом при решении сложных научных, технических и инженерных задач, а также при создании новых технологий и улучшении уже существующих.

Одной из областей, в которых математика применяется сейчас с большим успехом, является искусственный интеллект. Множество алгоритмов, разработанных математиками, находят свое применение при написании программ, которые могут анализировать и интерпретировать большие объемы данных, выполнять сложные операции, оптимизировать процессы и многое другое.

Кроме того, математика используется во многих областях науки и технологий, таких как криптография, биоинформатика, космические исследования, проектирование мостов и других сооружений. Она помогает точнее описывать реальные явления и процессы, и позволяет более эффективно решать сложные задачи, связанные с ними.

Таким образом, математика является неотъемлемой частью современной науки и технологий, и ее роль будет только расти в будущем. Поэтому, изучение и понимание математики должны стать одной из основ нашего образования, чтобы мы могли лучше понимать мир, в котором мы живем, и успешно применять математические методы в различных сферах нашей жизни.

Связь математики с природой

Математика – это наука, которая изучает структуру, форму, количество и отношения объектов и явлений. Она имеет прямое отношение к природе, поскольку многие явления, происходящие в природе, могут быть объяснены математически.

Различные физические процессы, такие как движение тел, взаимодействие частиц, распространение света и звука, описываются различными математическими законами. Математические инструменты и методы также используются в области географии, астрономии, экологии и других науках, связанных с природой.

Формальная логика, которая является основой математики, важна для понимания природы, поскольку она позволяет анализировать и описывать сложные явления и процессы. Кроме того, математика используется для моделирования и прогнозирования различных природных явлений, таких как изменения климата, распространение эпидемий и землетрясений.

Математика также имеет важное значение для понимания и изучения генетической информации, поскольку генетика сегодня часто использует математические методы для анализа генов и их взаимодействия.

Наконец, математика важна для понимания красоты и гармонии в природе. Многие законы математики находятся в основе симметрии и пропорциональности, которые в свою очередь являются основными элементами дизайна и архитектуры в природе. Например, золотое сечение, пропорция, которая используется в архитектуре и изобразительном искусстве, также связана с законами математики и рядом физических процессов.

Математические модели

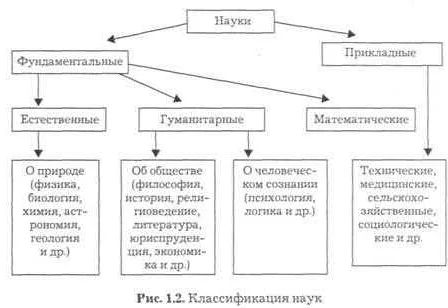
Математическая модель — это формализованное описание реальных или гипотетических процессов, которое основывается на математических методах и языке. Это позволяет исследовать различные сценарии и прогнозировать поведение системы в будущем.

Математические модели используются во многих областях науки, включая физику, экономику, биологию и, конечно же, математику. Наиболее известные примеры таких моделей — это уравнения Ньютона для описания движения тел, уравнения Максвелла в электродинамике и уравнения Шредингера в квантовой механике.

В математике модели могут быть использованы для вычисления численных значений решений уравнений, для доказательства теорем и для проверки идей на практике через имитационное моделирование. Они также могут быть использованы для представления информации в виде графиков и диаграмм, что позволяет наглядно изучать и анализировать различные зависимости и связи между данными.

В биологии математические модели играют важную роль в исследовании динамики популяций, роста и развития организмов, биохимических процессов и других явлений. Они могут помочь понять, какие факторы влияют на эти процессы и как можно управлять ими для достижения определенных результатов.

В экономике модели могут использоваться для прогнозирования экономического роста, инфляции и других финансовых индикаторов. Они также могут быть использованы для изучения взаимодействия между компаниями и потребителями, а также для анализа рынка и принятия решений о стратегии бизнеса.

Таким образом, математические модели играют важную роль в науке и промышленности, помогая исследователям и специалистам в различных областях принимать обоснованные решения в условиях неопределенности.

Принципы их создания

Аккуратность и точность. В математике каждый шаг должен быть предельно точным, поэтому при создании ее теорий, определений и формул, необходимо учитывать все детали и нюансы.

Логическое мышление. В математике важно следовать более общим принципам и правилам, а не запоминать конкретные решения. Это поможет при решении более сложных проблем.

Критический анализ и проверка результатов. Математика не имеет места для ошибок или неточностей, поэтому важно постоянно проверять результаты и делать корректировки.

Систематический подход. Математические теории и определения строятся на основе уже существующих, поэтому важно следовать установленным принципам и применять их в новых исследованиях.

Объективность и независимость. В математике важно руководствоваться только фактами и результатами, а не персональными предпочтениями или мнениями.

Примеры практического применения математических моделей

Математические модели имеют широкое применение во многих отраслях науки и техники. Они являются инструментом для анализа и прогнозирования различных процессов, а также для принятия решений. Рассмотрим несколько примеров практического применения математических моделей:

• Моделирование климата. С помощью математических моделей ученые могут прогнозировать изменения климата в будущем. Это позволяет государствам и международным организациям разрабатывать стратегии по снижению выбросов парниковых газов и защите окружающей среды.
• Финансовое моделирование. Математические модели используются в банковской и финансовой сфере для прогнозирования курса валют, изменения цен на акции, оценки рисков и разработки инвестиционных стратегий.
• Медицинское моделирование. В медицине математические модели могут помочь визуализировать внутренние органы и процессы в теле, а также предсказывать течение заболеваний и эффективность различных лечебных методов.
• Транспортное моделирование. С помощью математических моделей можно оптимизировать графики движения транспорта, разрабатывать новые маршруты и строить инфраструктуру, а также прогнозировать транспортный поток и обеспечивать безопасность на дорогах и в общественном транспорте.

Таким образом, математические модели являются важным инструментом для решения различных задач во многих областях науки и техники.

Математический анализ в исследовании природы

Математический анализ является одной из важнейших дисциплин в математике, а его применение в исследовании природы необходимо для понимания физических явлений и явлений в биологии. Многие природные процессы и явления описываются математическими моделями, которые основаны на понимании законов математического анализа.

Одним из примеров использования математического анализа в природных науках является анализ дифференциальных уравнений, часто используемых для описания физических процессов. Например, уравнения Ньютона описывают движение тел, а уравнения Максвелла — электромагнитные явления.

Другим примером может служить использование интегралов для определения площадей, объемов и других физических характеристик тел, таких как распределение заряда в проводнике или тепловой поток. Интегралы также используются для решения диффузионных уравнений, которые описывают различные процессы, связанные с диффузией вещества.

Математический анализ также имеет важное значение в биологии, например, для анализа роста популяций, мутаций генетических систем и прочих процессов в биологических системах. Использование статистических методов, основанных на математическом анализе, позволяет биологам сделать выводы о состоянии популяции или выборке и оценить значимость результатов исследования.

Таким образом, математический анализ является важным инструментом для понимания и анализа природных явлений и процессов, и его применение в исследовании природы будет постоянно расширяться с углублением наших знаний и технологического прогресса.

Роль математического анализа в физике и астрономии

Физика и астрономия — это науки, которые используют математические методы для описания и понимания природы. Науки эти тесно связаны с математикой, и одним из ключевых инструментов для их развития является математический анализ.

Математический анализ — это система методов, используемых для изучения функций, предельных значений и производных. Он является базой для многих теорий физики и астрономии.

Математические модели, основанные на математическом анализе, позволяют обнаруживать взаимосвязи между физическими явлениями и создавать прогнозы на основе математических законов. Так, математический анализ играет важную роль в понимании законов движения тел, электрических и магнитных полей, а также в изучении законов кинетики и термодинамики.

Астрономия также сильно опирается на математический анализ, так как астрономы используют его для расчета орбит планет, звезд и других космических объектов. Кроме того, математическое моделирование позволяет ученым прогнозировать поведение некоторых космических явлений, например, затмений.

Таким образом, продвижение физики и астрономии связано с использованием математического анализа. Без этого ключевого компонента невозможно было бы развивать науки, не было бы теорий и законов, а понимание природы было бы гораздо хуже.

Использование математического анализа в биологии и экологии

Математический анализ является неотъемлемой частью биологических и экологических исследований. Он помогает установить закономерности в функционировании живых систем и экосистем, а также понять и предсказать возможные изменения в них.

Одной из областей, где математический анализ широко применяется, является моделирование популяционных процессов. Индивиды могут взаимодействовать друг с другом, питаться, размножаться и умирать, а также подвергаться воздействию различных факторов, таких как изменения климата или наличие хищников. Математическое моделирование позволяет описать эти процессы, установить взаимосвязи между ними и предсказать, как изменения в одной области могут повлиять на другие.

Также математический анализ используется в экологии для изучения распределения и разнообразия видов, а также для анализа экологических систем. Например, математические модели позволяют прогнозировать, как изменения в земной атмосфере могут повлиять на изменение климата и, в результате, на функционирование экосистем. Они также могут помочь в определении оптимальных условий для выращивания растений или животных в различных условиях.

Таким образом, использование математического анализа в биологии и экологии играет важную роль в понимании живых систем и экосистем, а также приходит на помощь в принятии решений в области охраны окружающей среды и сельского хозяйства.

Математическая статистика в научном исследовании

Математическая статистика является неотъемлемой частью научных исследований, особенно в области естественных наук. Она позволяет извлечь информацию из данных и оценить вероятность определенных событий.

В научных исследованиях математическая статистика используется для анализа результатов экспериментов и определения степени уверенности в полученных результатах. Она позволяет проверить гипотезы и определить, являются ли результаты статистически значимыми или случайными.

Одна из важнейших задач математической статистики в научных исследованиях — это построение моделей, которые описывали бы изучаемые явления. Математические модели помогают предсказать результаты будущих экспериментов и сделать выводы о связи между различными явлениями.

1. Кроме того, математическая статистика позволяет:
   • Определить, насколько точны данные, полученные в ходе эксперимента;
   • Оценить, какой объем данных нужен для получения статистически значимых результатов;
   • Выделить основные закономерности, которые описывают данное явление.
2. Поэтому математическая статистика является неотъемлемой частью многих научных исследований и помогает ученым получать новые знания о мире вокруг нас.

Таким образом, математическая статистика играет ключевую роль в научном исследовании, позволяя ученым анализировать данные, определять статистическую значимость результатов и строить математические модели для описания изучаемых явлений.

Видео по теме:

Вопрос-ответ:

Как математика связана с природой?

Математика позволяет описывать природные явления и законы, а также предсказывать их поведение. Без математических методов невозможно было бы изучать многие области науки, связанные с природой, например, физику, астрономию, химию и др.

Как математика помогает в изучении генетики?

Математические модели используются в генетике для описания наследственности, расчета вероятности наследования генетических заболеваний и прогнозирования передачи генов от родителей к потомкам. Без математики генетические исследования были бы значительно затруднены.

Почему математика считается «языком науки»?

Математика позволяет выражать научные законы и теории в явном виде и формировать их в виде точных математических выражений. Она является удобным и эффективным инструментом для анализа и моделирования природных явлений и процессов.

Как математика помогает решать экологические проблемы?

Математические методы используются в экологических исследованиях для моделирования процессов взаимодействия биологических организмов и их окружения, оценки воздействия различных факторов на экосистему и определения оптимальных стратегий управления экосистемой.

Какая роль математики в физике?

Математика играет ключевую роль в физике, так как позволяет описывать физические законы и явления математически. Например, законы Ньютона, законы термодинамики и другие фундаментальные законы физики выражаются в математической форме.

Как математика используется в экономике?

Математические методы используются в экономике для моделирования процессов, прогнозирования экономических показателей, оптимизации решений и выработки стратегий управления экономическими системами. Без математических методов невозможно было бы решать многие экономические задачи.

Как математика связана с географией?

Математические методы используются в географии для моделирования географических процессов, составления карт и анализа пространственных данных. Например, при моделировании климатических изменений используются математические модели, а при составлении карт используется топологическая математика.

Основные понятия

Математика – это наука, которая исследует связи и законы между числами, формами, пространствами и переменными. Она охватывает множество областей, таких как алгебра, геометрия, теория вероятности и математическая логика.

Цифры – это символы, используемые для обозначения количества, которые можно складывать, вычитать, умножать или делить. Целые числа – это обычные числа без дробной части. Рациональные числа – это числа, которые можно представить в виде дроби.

Геометрия – это наука, изучающая отношения между фигурами и пространством. Она включает понятия, такие как точка, линия, поверхность, угол и объем. Геометрия широко используется в инженерных профессиях и проектировании.

Алгебра – это раздел математики, который изучает правила и символы для работы с абстрактными объектами. Алгебра используется для решения уравнений и систем уравнений.

Теория вероятности – это отрасль математики, которая изучает случайные события и вероятность их возникновения. Она используется в статистике, физике, экономике и других областях.

Математическая логика – это наука, которая изучает способы представления математических высказываний и рассуждений. Она играет важную роль в разработке программного обеспечения и технологий искусственного интеллекта.

Все эти области математики тесно связаны между собой и играют важную роль в решении задач как в научных, так и в практических областях.

Примеры применения математической статистики в различных областях науки

Математическая статистика является одной из ключевых областей математики, которая используется для анализа данных и получения выводов на основе вероятностных распределений. Ниже описаны несколько примеров такого применения в различных областях науки.

• Медицина: математическая статистика используется для анализа результатов испытаний медицинских препаратов и для оценки эффективности лечения. Также она может быть использована для исследования причин заболеваний и оценки вероятности развития заболеваний у пациентов.
• Физика: математическая статистика используется для моделирования физических процессов и анализа результатов экспериментов. Кроме того, статистические методы применяются для нахождения закономерностей в данных, полученных с помощью различных исследовательских приборов.
• Экономика: математическая статистика используется для анализа экономических данных и прогнозирования экономических событий. Статистические методы могут помочь выявить закономерности в поведении рынков и потребителей, а также принять важные решения в области бизнеса.
• Биология: математическая статистика используется для анализа больших объемов данных, полученных из геномных исследований, и для оценки вероятности возникновения различных заболеваний. Статистические методы могут также помочь изучить взаимодействие между различными видами живых организмов.

Как видно, математическая статистика играет важную роль в многих областях науки и помогает ученым сделать выводы на основе сложных данных. Благодаря этому, статистические методы признаны неотъемлемой частью современной науки и технологий.