Математика профиль что нужно знать
Содержимое
- 1 Математика профиль что нужно знать
- 1.1 Математика профиль: основные положения
- 1.2 Видео по теме:
- 1.3 Профиль математики в школе
- 1.4 Важность изучения математики
- 1.5 Основные понятия в математике
- 1.6 Алгебра и геометрия
- 1.7 Практическое применение математики
- 1.8 Математика и карьера
- 1.9 Современные требования к знанию математики
- 1.10 Как успешно изучать математику профиль
- 1.11 Вопрос-ответ:
Статья рассказывает о важности изучения математики в профильном образовании, а также о основных понятиях и навыках, которые необходимо знать, чтобы успешно учиться в данной области. Она также подробно описывает применение математики в различных профессиях и повседневной жизни, демонстрируя ее значимость и практичность.
Математика — одна из основных дисциплин, которую изучают в школе. Однако, многие ученики часто задаются вопросом, зачем им нужно изучать математику, особенно если они не планируют связать свою будущую профессию с этой наукой. Ответ на этот вопрос прост — математика является неотъемлемой частью нашей жизни и необходима во многих областях деятельности.
Математика, безусловно, является основой для многих профессий, связанных с наукой и технологией. Например, инженеры, архитекторы, программисты и ученые используют математические знания для решения сложных задач и разработки новых технологий.
Однако, математика также полезна и в повседневной жизни. Навыки решения математических задач помогают развивать логическое мышление, аналитические способности и критическое мышление. Они помогают нам принимать взвешенные решения и решать проблемы в различных ситуациях.
Поэтому, даже если вы не планируете стать математиком, знание основных математических понятий и навыков будет полезным для вас в жизни и карьере. В этой статье мы рассмотрим основные темы математики профильного уровня, которые помогут вам лучше понять эту науку и ее применение в реальной жизни.
Математика профиль: основные положения
В профильной математике важно усвоить не только базовые знания, но и понять основные положения и принципы, которые лежат в основе этой науки. Основные положения включают в себя следующие аспекты:
- Алгебра: изучение алгебраических операций (сложение, вычитание, умножение, деление), алгебраических выражений, уравнений, систем уравнений, функций и их свойств.
- Геометрия: изучение фигур, их свойств и отношений, а также изучение геометрических операций (построение, измерение, анализ).
- Тригонометрия: изучение отношений между сторонами и углами в треугольниках, а также функций, связанных с этими отношениями.
- Математический анализ: изучение предельных и производных значений функций, а также их приложений в различных областях, таких как физика, экономика и т. д.
Правильное понимание и усвоение этих основных положений поможет студентам успешно продвигаться в изучении математики и решать сложные проблемы и задачи, как в школе, так и в дальнейшем профессиональном образовании.
Видео по теме:
Профиль математики в школе
Профиль математики включает в себя изучение различных разделов математики, таких как алгебра, геометрия, математический анализ, теория вероятностей и другие. Ученикам также предлагается углубленное изучение основных теоретических концепций и методов математики.
Одним из основных направлений профиля математики является алгебра. Ученики изучают различные алгебраические структуры, такие как множества, группы, кольца и поля. Учатся решать уравнения и неравенства, проводить операции с комплексными числами, изучают теорию многочленов и рациональных функций.
Геометрия также занимает важное место в профиле математики. Ученики изучают различные фигуры, свойства прямых и плоскостей, геометрические преобразования, тригонометрические функции и другие темы. Геометрия позволяет ученикам развивать пространственное мышление и умение работать с геометрическими объектами.
Математический анализ – это раздел математики, который изучает пределы, производные, интегралы и другие математические концепции. Ученики изучают основные принципы математического анализа и применяют их для решения различных задач.
В профиле математики ученики также знакомятся с теорией вероятностей и математической статистикой. Они изучают вероятностные модели, анализируют случайные события, решают задачи на определение вероятностей и проводят статистические исследования.
Изучение профиля математики в школе открывает множество возможностей для дальнейшего образования и профессиональной карьеры. Математические знания и навыки могут быть применены во многих областях, таких как физика, экономика, компьютерные науки и др.
Преимущества профиля математики:
| Развитие логического мышления и аналитических способностей |
| Формирование навыков решения задач и критического мышления |
| Возможность продолжить обучение в высших учебных заведениях |
| Широкий спектр применения математических знаний в различных областях |
Важность изучения математики
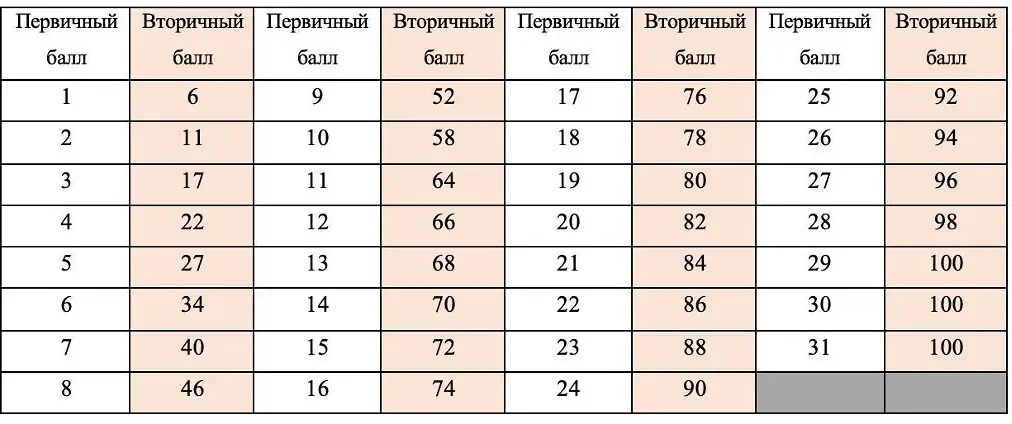
Изучение математики помогает развить навыки решения задач, анализа данных, прогнозирования и принятия решений. Оно также развивает навыки работы с числами, расчетов и измерений, которые являются необходимыми во многих сферах деятельности, включая науку, инженерию, экономику и финансы.
Кроме того, изучение математики помогает развить навыки коммуникации и сотрудничества, так как многие математические задачи могут быть решены в группе. Оно также способствует развитию терпения, усидчивости и настойчивости, так как решение некоторых математических задач может потребовать много времени и усилий.
Изучение математики также помогает развить воображение и креативное мышление. Математика включает в себя различные концепции и идеи, которые могут быть применены для создания новых решений и идей. Оно также помогает развить навыки моделирования и представления данных, что является важным в современном мире, где большое количество информации требует анализа и интерпретации.
В целом, изучение математики является важным элементом образования, который помогает развить широкий спектр навыков и качеств, необходимых для успешной карьеры и личностного развития.
Основные понятия в математике

Одним из основных понятий в математике является число. Числа могут быть натуральными, целыми, рациональными и иррациональными. Натуральные числа — это числа, которые используются для подсчета и обозначают количество элементов в множестве. Целые числа включают в себя как натуральные числа, так и их отрицания, а также число ноль. Рациональные числа — это числа, представленные дробями, в которых числитель и знаменатель являются целыми числами. Иррациональные числа — это числа, которые не могут быть представлены в виде десятичной дроби и имеют бесконечное количество десятичных знаков.
Понятие операции связано с процессом преобразования чисел с использованием определенных правил. Операции включают в себя сложение, вычитание, умножение и деление. Сложение позволяет объединять числа или множества, вычитание — находить разность между числами или множествами, умножение — находить произведение чисел или множеств, а деление — находить отношение между числами или множествами. Операции могут быть применены к различным типам чисел и объектов.
Понятие функции является одним из основных в математике. Функция представляет собой отображение между двумя множествами, где каждому элементу первого множества соответствует единственный элемент второго множества. Функции могут быть представлены графически, алгебраически или в виде таблицы значений. Они играют важную роль в моделировании и анализе различных процессов и явлений.
- Интеграл
- Производная
- Теория вероятности
- Геометрия
- Тригонометрия
Это лишь некоторые из основных понятий в математике, которые служат основой для изучения этой науки. Изучение и понимание этих понятий позволяет строить более сложные модели и решать более сложные проблемы в различных областях знаний.
Алгебра и геометрия
В алгебре изучаются такие понятия, как переменная, алгебраическое выражение, уравнение, система уравнений, функция и многое другое. Алгебра позволяет решать различные математические задачи, используя символы и операции над ними. Она также широко применяется в физике, экономике, компьютерных науках и других областях.
Геометрия, в свою очередь, изучает формы, размеры, отношения и свойства геометрических фигур и пространств. Она включает в себя такие понятия, как точка, линия, плоскость, угол, треугольник, окружность и многое другое. Геометрия позволяет анализировать и решать задачи, связанные с расположением объектов в пространстве, а также строить различные геометрические построения.
Алгебра и геометрия тесно связаны между собой. Некоторые задачи могут быть решены с использованием методов и понятий обеих областей математики. Например, для решения геометрической задачи может потребоваться использование алгебраических выражений и уравнений. И наоборот, алгебра может быть использована для анализа и решения геометрических задач.
Овладение навыками в области алгебры и геометрии является важным для понимания и решения различных математических задач. Знание этих дисциплин помогает развивать абстрактное мышление, логическое мышление, аналитические навыки и способности к решению проблем. Оно также может быть полезным при изучении других наук и применении математических методов в реальной жизни.
Практическое применение математики
Одним из основных применений математики является ее использование в научных исследованиях. Математические модели позволяют ученым описывать и предсказывать различные явления и процессы. Например, математические модели помогают прогнозировать погоду, расчеты при строительстве сооружений, моделирование физических систем и многое другое.
Математика также является неотъемлемой частью финансовой сферы. Банки, инвестиционные компании и страховые организации используют математические методы для анализа рисков, прогнозирования доходности, определения стоимости активов и принятия финансовых решений.
Технологическая индустрия тоже невозможна без математики. Математические алгоритмы применяются в различных областях, начиная от разработки программного обеспечения и создания компьютерных игр до анализа данных и искусственного интеллекта. Математика также является основой для различных методов шифрования информации и криптографии.
Математика находит свое применение и в медицине. Она используется для моделирования и анализа биологических систем, прогнозирования распространения болезней, оптимизации планов лечения и многое другое.
Но не только профессионалы нуждаются в математике. Она также пригодится в повседневной жизни. Например, при покупке товаров со скидкой, в расчете бюджета, при планировании поездок или при решении бытовых задач.
В заключение можно сказать, что знание математики является необходимым навыком в современном мире. Она помогает развивать логическое мышление, улучшает абстрактное и критическое мышление, а также помогает решать сложные задачи и принимать обоснованные решения.
Математика и карьера

Математические знания могут быть полезными при выборе профессии и развитии карьеры. Во многих областях работы требуется умение мыслить логически, анализировать информацию и принимать решения на основе данных. Математика помогает развить эти навыки и дает преимущество при поиске работы.
Многие профессии напрямую связаны с математикой. Например, инженеры, программисты, финансисты и экономисты часто используют математические методы и модели в своей работе. Они решают задачи оптимизации, моделирования и анализа данных, которые требуют глубокого понимания математических концепций.
Однако математика может быть полезной не только в профессиях, прямо связанных с ней. Математические навыки помогают развивать абстрактное мышление, логику и креативность, что полезно во многих областях жизни. Решение математических задач требует терпения, настойчивости и системного подхода, что развивает дисциплину и самоорганизацию.
Кроме того, математические знания могут быть основой для изучения других наук. Физика, химия, биология и многие другие дисциплины используют математические модели и методы для объяснения и предсказания явлений в природе. Понимание математики помогает лучше понять мир вокруг нас и научиться анализировать сложные процессы и законы природы.
Таким образом, математика играет важную роль в различных сферах жизни и карьеры. Независимо от выбранной профессии, математические знания помогут развить аналитическое мышление, прогнозирование и принятие решений, что является ключевыми навыками в современном мире.
Современные требования к знанию математики
Современные требования к знанию математики не ограничиваются только основными арифметическими операциями и решением простых уравнений. Вместо этого, требуется глубокое понимание математических концепций, умение анализировать сложные задачи и применять методы решения.
Одним из основных требований является понимание алгебры и геометрии. Умение работать с алгебраическими выражениями, решать уравнения и неравенства, анализировать и доказывать геометрические теоремы является необходимым для успешного продвижения в математической сфере.
Кроме того, требуется знание математического анализа. Он включает в себя дифференциальное и интегральное исчисление, а также теорию пределов и рядов. Понимание этих концепций не только позволяет решать сложные математические задачи, но и является основой для понимания физических и экономических явлений.
Компьютерные науки и статистика также требуют глубокого знания математики. Умение работать с алгоритмами, решать задачи оптимизации и анализировать статистические данные является необходимым для успешного применения математических методов в этих областях.
В целом, современные требования к знанию математики ставят перед учащимися высокие стандарты. Но обладая глубокими знаниями и умениями в этой области, можно быть востребованным специалистом во многих сферах деятельности.
Как успешно изучать математику профиль
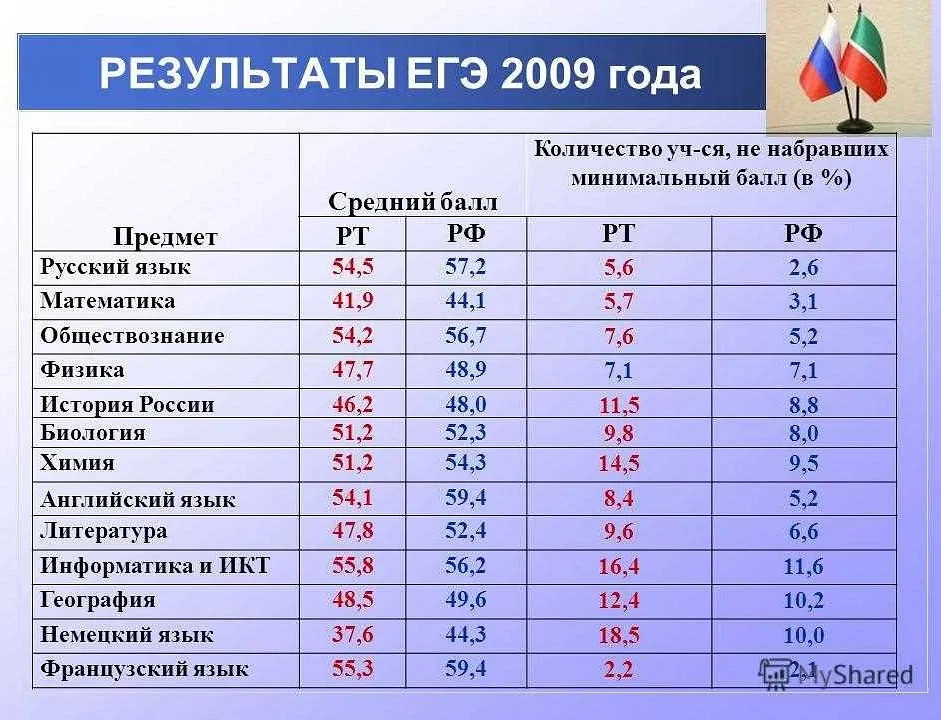
Изучение математики профильного уровня может быть вызовом для многих студентов. Этот предмет требует особого подхода и глубокого понимания математических концепций. Вот несколько советов о том, как успешно изучать математику профиль:
- Создайте расписание. Регулярное изучение математики профильного уровня является ключом к успеху. Создайте расписание и придерживайтесь его. Уделите достаточно времени для повторения и выполнения практических заданий.
- Понимайте основные концепции. Математика профильного уровня строится на фундаментальных концепциях. Убедитесь, что вы хорошо понимаете эти концепции, иначе позже вам будет сложнее разбираться в более сложных темах.
- Решайте много практических заданий. Практика — это ключ к успеху в математике. Решайте много задач, чтобы закрепить свои знания и навыки. Изучение только теории не даст вам достаточного понимания материала.
- Сотрудничайте с другими студентами. Обсуждайте математические задачи с другими студентами из вашего класса. Это поможет вам получить разные подходы к решению проблемы и понять ее с разных точек зрения.
- Используйте различные источники материалов. Изучение математики профильного уровня может быть сложным, поэтому не ограничивайтесь только учебником. Используйте различные источники, такие как онлайн-курсы, видеоуроки или дополнительные учебники, чтобы получить более глубокое понимание темы.
Следуя этим советам, вы можете успешно изучать математику профильного уровня и достичь хороших результатов. Важно помнить, что практика и стойкость имеют ключевое значение в достижении успеха в этом предмете.
Вопрос-ответ:
Какие предметы являются основой для изучения математики?
Основой для изучения математики являются предметы, такие как алгебра, геометрия, математический анализ, теория вероятностей и др.
Для чего нужно изучать математику?
Изучение математики развивает логическое мышление, умение анализировать информацию, решать сложные задачи, а также находить логические связи и закономерности в различных областях жизни.
Какие навыки можно получить, изучая математику?
Изучение математики позволяет развить навыки анализа, логического мышления, решения задач, умение работать с числами и формулами, а также понимание математических моделей и их применение в реальной жизни.
Какие профессии связаны с математикой?
Математика может быть полезна во многих профессиях, таких как программист, аналитик данных, финансовый аналитик, инженер, статистик, ученый, преподаватель и многие другие.
Какие конкретные темы изучаются в математике?
В математике изучаются различные темы, такие как алгебраические уравнения, геометрия, тригонометрия, матрицы, дифференциальные уравнения, вероятность и статистика, численные методы и многое другое.
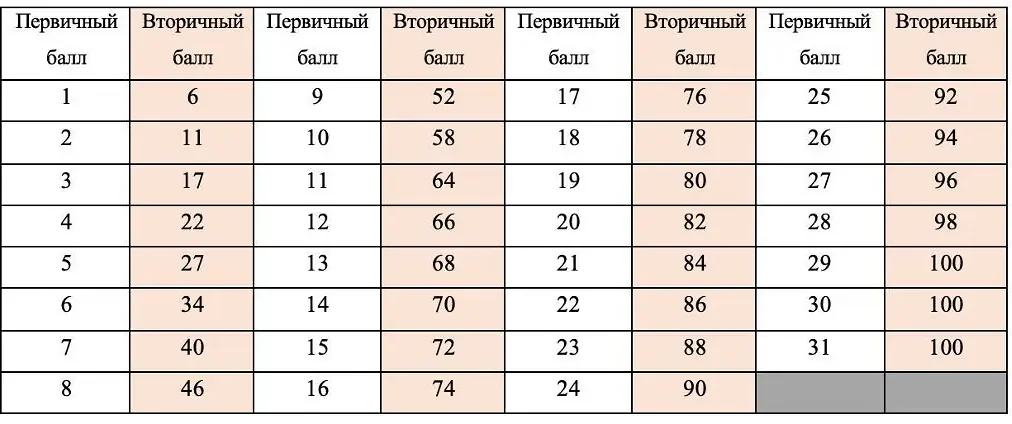




Спасибо за статью! Очень интересно узнать, что включает в себя профиль математики. Я всегда считал математику одним из самых важных предметов, но не знал, что она может иметь такое разнообразие приложений. Узнать, что она используется в экономике, физике, компьютерных науках и других областях, действительно впечатляет. Теперь мне стало интересно узнать больше о дифференциальных уравнениях и графовой теории. Статья также дала мне понимание того, что навыки в математике могут быть полезными не только для работы, но и для принятия решений в повседневной жизни. Я обязательно буду учиться и развивать свои математические навыки, чтобы лучше понимать и анализировать мир вокруг меня.
Статья очень понравилась! Я всегда считал математику сложной и непонятной наукой, но после ее прочтения у меня появился интерес к изучению этого предмета. В статье хорошо описаны основные концепции и принципы математики, которые нужно знать. Теперь я понимаю, что математика — это не просто скучные формулы и уравнения, а наука, которая помогает нам понять мир вокруг нас. Мне понравилось, как автор статьи объясняет сложные концепции математики простым и понятным языком. Он дает примеры и иллюстрации, которые помогают лучше понять материал. Также мне понравилось, что статья не только объясняет основные концепции математики, но и показывает, как они применяются на практике. Это позволяет лучше понять, зачем нужно изучать этот предмет. Я думаю, что эта статья будет полезна как студентам, изучающим математику в школе или вузе, так и тем, кто просто интересуется этой наукой. Статья помогает осознать, что математика — это не только предмет для умных и талантливых, но и предмет, который каждый может изучать и понимать. В целом, статья очень познавательная и интересная. Она помогает изменить отношение к математике и показывает, что она не такая уж и сложная. Я поделился этой статьей с друзьями и они тоже были приятно удивлены, насколько интересно и понятно она написана. Спасибо автору за такую полезную и понятную статью!