Математика руками как называется
Содержимое
- 1 Математика руками как называется
- 1.1 История математики: открытия и достижения
- 1.2 Принципы математики и их применение
- 1.3 Роль математики в ежедневной жизни
- 1.4 Основные понятия и термины в математике
- 1.5 Математические методы и их классификация
- 1.6 Математика в различных науках и отраслях
- 1.7 Математические задачи и их решение
- 1.8 Перспективы развития математики в будущем
- 1.9 Вопрос-ответ:
- 1.10 Видео по теме:
Математика руками – это метод обучения математике, который основан на использовании рук и конкретных предметов для визуализации и понимания математических концепций. Узнайте, как этот метод называется и как он может помочь вашему ребенку лучше понять и запомнить математику.
Математика руками – это метод обучения и практики математики, который основан на использовании рук и пальцев для решения математических проблем. Этот подход позволяет детям и взрослым лучше понять математические концепции и развить свои навыки решения задач.
Основная идея математики руками заключается в том, что каждый палец на руке соответствует определенной цифре от 0 до 9. Руки используются для представления чисел и выполнения различных математических операций, таких как сложение, вычитание, умножение и деление.
Математика руками имеет много преимуществ. Она помогает развить у детей и взрослых навыки концентрации, воображения и логического мышления. Этот метод также помогает улучшить память и умение решать задачи быстрее и точнее. Кроме того, математика руками может быть интересной и веселой игрой для всех возрастов.
Математика руками имеет множество различных терминов и методов, включая абакус, цифровое представление, алгоритмы и многое другое. Использование этих методов помогает улучшить понимание математических концепций и развить уверенность в решении задач.
История математики: открытия и достижения
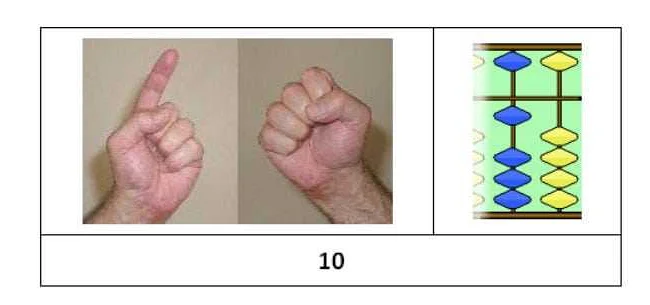
Одним из первых великих достижений в математике было открытие десятичной системы счисления. Эта система, основанная на использовании десяти различных цифр, позволила людям проводить арифметические операции и решать сложные математические задачи. Более того, она обеспечила основу для развития других областей математики, таких как геометрия и алгебра.
В древнем Египте и Месопотамии математика использовалась для решения практических задач, таких как измерение земельных участков и строительство пирамид. В Индии и Китае были разработаны системы счисления, а также осуществлены важные открытия в области алгебры и геометрии.
В Древней Греции математика стала объектом философских исследований. Великие ученые, такие как Пифагор, Евклид и Архимед, разработали фундаментальные теоремы и методы решения математических задач. Например, Пифагорова теорема о треугольниках или закон Архимеда.
В средние века математика продолжала развиваться, тем не менее, она оставалась относительно независимой от других наук. Важными достижениями этого периода стали разработка алгебры и тригонометрии.
С появлением новых научных методов в эпоху Просвещения математика стала играть все более важную роль в различных областях науки. Были открыты новые математические концепции и методы, такие как интеграл и дифференциал, и разработаны новые области математики, такие как математический анализ и теория вероятностей.
В 20-м и 21-м веках математика продолжает развиваться, и современные математики продолжают делать новые открытия и достигать впечатляющих результатов. Одним из самых известных достижений последних лет является решение гипотезы Пуанкаре — одной из самых сложных и долго нерешенных задач в области топологии и геометрии. Это доказательство потребовало использования сложных математических техник и компьютерных вычислений.
История математики — это история открытий и достижений умных и целеустремленных людей, которые стремились понять природу чисел и форм, исследовать законы математической логики и применить свои знания для решения сложных задач. Благодаря их труду математика стала неотъемлемой частью нашей жизни и науки.
Принципы математики и их применение
- Аксиомы: это независимые и неопровержимые утверждения, которые принимаются без доказательства и являются основой для построения математической теории.
- Определения: это формальные описания математических понятий, которые четко и однозначно определяют их свойства и характеристики.
- Теоремы: это утверждения, которые могут быть доказаны на основе аксиом и определений. Теоремы являются основными результатами математической науки и позволяют выводить новые факты и свойства.
- Доказательства: это логические аргументы, которые позволяют убедиться в истинности или ложности математического утверждения. Доказательства основаны на логических законах, аксиомах и предыдущих теоремах.
Принципы математики имеют широкое применение в различных областях науки и техники. Они используются для моделирования сложных систем, решения оптимизационных задач, разработки алгоритмов, анализа данных и многих других приложений. Математические методы позволяют точно и объективно описывать и изучать явления и объекты, предсказывать их поведение и принимать обоснованные решения на основе полученных результатов.
Роль математики в ежедневной жизни

Математика играет важную роль в нашей ежедневной жизни. Она помогает нам развивать логическое мышление, анализировать информацию и принимать обоснованные решения. Без математики было бы трудно представить себе наше существование в современном мире.
В повседневной жизни математика применяется в различных сферах. Она помогает нам считать деньги, планировать бюджет, рассчитывать время и расстояния. Математика нужна при покупке товаров с распродажи, чтобы рассчитать итоговую стоимость с учетом скидки. Она также используется в кулинарии для измерения ингредиентов и рассчета времени приготовления блюд.
Математика помогает нам разбираться в финансовых вопросах, таких как кредиты, ипотеки, инвестиции. Она позволяет нам рассчитывать проценты, сумму платежей и оценивать риски. Математика также применяется в налоговой сфере, где рассчитываются налоги и сборы.
Математика важна для планирования и организации. Она помогает нам составлять графики и диаграммы, строить планы и расписания. Математические расчеты позволяют оптимизировать процессы и увеличивать эффективность работы.
Математика также играет важную роль в науке и технологиях. Она используется для моделирования и прогнозирования различных явлений, от погоды до экономики. Без математических расчетов было бы трудно проводить исследования и разрабатывать новые технологии.
Кроме того, математика развивает наше мышление, учит нас анализировать информацию, решать проблемы и находить новые подходы к решению задач. Она помогает нам развивать логику, абстрактное мышление и креативность. Математические задачи тренируют наш мозг и помогают нам развивать навыки, которые пригодятся нам во многих сферах жизни.
Таким образом, математика является неотъемлемой частью нашей ежедневной жизни. Она помогает нам развиваться и преуспевать в различных сферах деятельности. Поэтому важно уделять ей достаточно внимания и не бояться использовать ее в повседневных задачах.
Основные понятия и термины в математике
Один из основных терминов в математике — это число. Число — это абстрактный объект, который используется для обозначения количества или меры. В математике существуют различные типы чисел, такие как натуральные числа, целые числа, рациональные числа и действительные числа.
Другой важный термин — это операция. Операция — это действие или процесс, который выполняется над числами или другими математическими объектами. Операции могут быть такими как сложение, вычитание, умножение и деление. Они играют важную роль в выполнении математических вычислений и решении задач.
Также существуют понятия в математике, связанные с отношениями и свойствами объектов. Например, равенство — это отношение между двумя объектами, которые имеют одинаковую величину или значение. Неравенство — это отношение между двумя объектами, которые имеют различную величину или значение.
Еще одно важное понятие — это функция. Функция — это отображение между двумя множествами, где каждому элементу первого множества сопоставляется элемент второго множества. Функции играют ключевую роль в математическом моделировании и анализе данных.
Это только небольшая часть основных понятий и терминов в математике. Понимание и использование этих терминов является ключевым для изучения и применения математических методов и решения задач во многих областях науки и техники.
Математические методы и их классификация

Математические методы можно классифицировать по различным критериям. Одним из основных критериев классификации является область применения метода. В зависимости от области применения математические методы могут относиться к следующим категориям:
- Алгебраические методы. Это методы, основанные на алгебраических операциях и свойствах чисел. Алгебраические методы используются для решения уравнений, систем уравнений, а также для работы с алгебраическими структурами, такими как группы, кольца и поля.
- Геометрические методы. Геометрические методы используются для изучения и анализа геометрических объектов и их свойств. Эти методы включают в себя использование геометрических преобразований, координатной геометрии, а также аналитической геометрии.
- Вероятностные методы. Это методы, связанные с вероятностью и статистикой. Они используются для анализа случайных явлений, моделирования вероятностных событий и прогнозирования.
- Аналитические методы. Аналитические методы используются для изучения функций и их свойств с помощью математического анализа. Они включают дифференциальное и интегральное исчисление, теорию пределов и рядов.
- Комбинаторные методы. Комбинаторные методы используются для изучения комбинаторных объектов и их свойств. Они включают в себя комбинаторику, теорию графов и теорию кодирования.
Кроме того, математические методы могут быть классифицированы по тому, как они применяются. Например, существуют методы решения задач оптимизации, методы численного анализа, методы математической логики и другие.
Классификация математических методов позволяет систематизировать и организовать знания в математике, а также выбрать наиболее подходящий метод для решения конкретной задачи. Благодаря этому математика становится более доступной и удобной для использования в различных областях науки, техники и практики.
Математика в различных науках и отраслях

В физике математика используется для описания физических явлений и разработки математических моделей. Она позволяет установить законы природы и предсказать результаты экспериментов. Без математических методов невозможно понять и объяснить основные принципы физики.
Химия также тесно связана с математикой. Она используется для анализа химических реакций, расчета состава и свойств веществ. Математические модели позволяют прогнозировать результаты химических экспериментов и оптимизировать процессы.
Биология использует математику для моделирования и анализа биологических систем, таких как генетические сети, эволюция организмов и популяционная динамика. Математические методы помогают понять сложные биологические процессы и выявить закономерности.
В экономике и финансах математические модели используются для анализа рынков, прогнозирования цен и доходности инвестиций. Математика позволяет оптимизировать бизнес-процессы и принять обоснованные решения.
Компьютерные науки и информатика сильно опираются на математику. Она используется для разработки алгоритмов, шифрования данных, оптимизации вычислений и создания искусственного интеллекта. Математика является основой для развития современных информационных технологий.
Математика также широко применяется в инженерии, географии, социологии, психологии и других науках. Она помогает анализировать данные, строить модели и принимать обоснованные решения.
Математические задачи и их решение
Математические задачи представляют собой конкретные ситуации или вопросы, которые требуют решения с использованием математических методов и понятий. Решение математической задачи включает в себя последовательность логических шагов, направленных на достижение конечного результата.
Существует множество различных типов математических задач, включая задачи на нахождение неизвестного значения, задачи на определение зависимостей и связей между величинами, задачи на нахождение максимального или минимального значения, задачи на расчет вероятностей и многое другое.
Решение математической задачи обычно включает в себя следующие этапы:
- Понимание условия задачи и выделение важных данных.
- Формулирование математической модели для решения задачи.
- Разработка плана решения, включающего необходимые формулы, методы и подходы.
- Выполнение вычислений и анализ полученных результатов.
- Проверка ответа и его интерпретация в контексте задачи.
Важно отметить, что решение математической задачи может быть не единственным, и существуют различные подходы и методы для достижения результата. Однако, в основе решения любой задачи лежит применение математических знаний и навыков, логическое мышление и аналитические способности.
Решение математических задач имеет важное практическое значение и находит свое применение во многих областях жизни, включая науку, технику, экономику и финансы, социальные и гуманитарные науки и т.д. Поэтому развитие навыков решения математических задач является важной задачей образования и требует от студентов и учащихся усердия, терпения и настойчивости.
Перспективы развития математики в будущем
Математика, как наука, постоянно развивается и находит новые применения в различных областях жизни. В будущем ожидаются следующие перспективы развития математики:
- Развитие компьютерных технологий и искусственного интеллекта позволит создавать более мощные и быстрые алгоритмы для решения сложных математических задач. Это откроет новые возможности для исследований и применения математики в различных областях науки и техники.
- Расширение области применения математики в экономике и финансовой сфере. В условиях быстро меняющегося мира и глобализации экономики, математические модели и методы становятся все более востребованными для прогнозирования экономических процессов, управления финансовыми рисками и принятия решений.
- Развитие математической биологии и медицины. Математические модели и методы позволяют лучше понимать сложные биологические процессы и динамику распространения заболеваний. Это может привести к появлению новых методов диагностики и лечения, а также к разработке лекарственных препаратов.
- Применение математических методов в сфере искусственного интеллекта и машинного обучения. Математические алгоритмы играют ключевую роль в разработке и обучении искусственных нейронных сетей, которые могут быть использованы для решения сложных задач распознавания образов, обработки естественного языка и принятия решений.
- Развитие криптографии и квантовых вычислений. В условиях развития интернета и цифровых технологий, защита информации становится все более актуальной. Криптографические методы и алгоритмы, основанные на математических принципах, помогают обеспечить безопасность передачи и хранения данных. Развитие квантовых вычислений может привести к созданию новых криптографических методов, которые будут устойчивы к атакам квантовых компьютеров.
В целом, математика будет продолжать играть важную роль в науке, технике, экономике и других областях жизни. Развитие новых методов и приложений математики будет способствовать прогрессу и улучшению качества жизни людей в будущем.
Вопрос-ответ:
Что такое математика руками?
Математика руками — это методика обучения математике, в которой ребенок использует свои руки для создания и исследования различных математических концепций. Она основана на идее, что физическое взаимодействие с математическими объектами помогает усвоить и понять абстрактные математические понятия.
Какая методика обучения математике с использованием рук существует?
Одна из самых популярных методик обучения математике с использованием рук — это методика Монтессори. В этой методике дети используют специальные материалы, такие как цветные палочки, бусины и блоки, чтобы создавать и изучать различные математические концепты. Они могут складывать, вычитать, умножать и делить с помощью этих предметов, что помогает им лучше понять эти операции.
Какие преимущества имеет методика математики руками?
Методика математики руками имеет несколько преимуществ. Во-первых, она помогает развить у детей пространственное мышление и моторику рук. Во-вторых, она позволяет детям лучше понять и запомнить математические концепты, благодаря физическому взаимодействию с математическими объектами. В-третьих, она делает обучение математике более интересным и увлекательным, так как дети могут видеть и ощущать результат своей работы.
Как можно применять методику математики руками на практике?
Методику математики руками можно применять на практике, используя различные математические игры и задания. Например, дети могут использовать цветные блоки для складывания и вычитания чисел, совершая физические действия соответствующие операциям. Они также могут использовать бусины для создания и изучения шаблонов и последовательностей. Главное — дать детям возможность самостоятельно исследовать и экспериментировать с математическими концепциями с помощью своих рук.
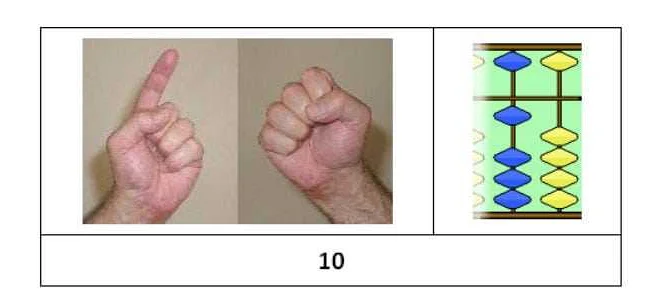



«Математика руками: что такое и как она называется?». Очень интересная статья, я всегда был увлечен математикой и рад, что смог узнать о таком необычном подходе к изучению этой науки. Когда я впервые услышал о математике руками, я был немного смущен, но сейчас понимаю, что это нечто новое и необычное. Этот метод объединяет математику с искусством и физическим восприятием, что делает ее более доступной и интересной. Математика руками — это способ изучения математики, при котором используются конкретные объекты и ручной труд. Вместо того, чтобы просто смотреть на числа и символы на бумаге, мы можем физически создавать геометрические фигуры, моделировать функции и проводить различные эксперименты. Это помогает нам более глубоко понять и запомнить математические концепции. Кроме того, математика руками имеет свое собственное название — «манипулятивная математика». Это слово происходит от латинского слова «manipulus», что означает «рукопожатие» или «взаимодействие». Очень подходящее название, потому что именно взаимодействие с математическими объектами помогает нам лучше понять их свойства и взаимосвязи. Математика руками может быть использована как в школьном образовании, так и при самостоятельном изучении. Она помогает развить у детей и взрослых логическое мышление, воображение и креативность. К тому же, она делает математику более визуальной и понятной, что помогает преодолеть страх перед этой наукой. Я уверен, что математика руками — это важный и интересный подход к изучению математики, который может быть полезен для всех. Я намерен попробовать его самостоятельно и рекомендую всем, кто интересуется математикой, сделать то же самое. Это новый способ взглянуть на старую и очень важную науку.
Очень интересная статья! Я всегда увлекалась математикой, и когда узнала о существовании математики руками, я восхитилась. Теперь я понимаю, что это не просто метод счета на пальцах, а настоящая наука. Невероятно, каким образом можно решать сложные математические задачи, используя только свои руки! Это явно требует большого навыка и тренировки. Я с нетерпением жду, чтобы попробовать этот метод и улучшить свои математические навыки. Большое спасибо за информативную статью!