Математика наука которая была особенно хорошо развита в древней индии

Математика в Древней Индии достигла высокого уровня развития и имела значительное влияние на развитие науки. Ученые индийской цивилизации разработали сложные алгоритмы, системы счета и математические методы, которые использовались в различных областях знаний. Изучение истории математики в Древней Индии позволяет лучше понять основные принципы и достижения этой древней науки.

Математика в Древней Индии имеет богатую историю развития и значимые достижения. Согласно историческим источникам, первые упоминания о математике в Индии относятся к Ведическому периоду (1500–500 гг. до н.э.), когда были созданы первые математические трактаты. Однако наиболее значимое развитие математики произошло в период с IV до XII веков н.э., когда были созданы великие труды, влияние которых ощущается и по сей день.

Одним из наиболее известных математиков Древней Индии был Арифметика (VII век н.э.), автор знаменитого трактата «Лилавати». В этом труде Арифметика представил множество математических задач и методов их решения. Он внес значительный вклад в развитие алгебры и теории чисел, а также предложил методы решения квадратных уравнений и систем линейных уравнений.

Математика в Древней Индии была не только прикладной, но и теоретической. Ученые Индии достигли значительных успехов в области численных методов, геометрии, алгебры, астрономии и теории вероятности.

Еще одним важным достижением в области математики в Древней Индии была разработка десятичной системы счисления. Эта система считается одной из величайших математических открытий человечества и имеет решающее значение для развития математики и других наук. Вместе с десятичной системой счисления в Индии были открыты и другие математические концепции, такие как нуль, десятичные дроби, бесконечные десятичные разложения и др.

История развития математики в Древней Индии

Древняя Индия считается одной из самых важных цивилизаций, в которой была развита математика. Одним из первых текстов, связанных с математикой, был «Сулба-сутры», написанный около 800 года до нашей эры. Этот текст содержал геометрические правила для строительства алтарей, что демонстрирует глубокое понимание принципов геометрии в Древней Индии.

В 5 веке до нашей эры индийский математик Аристотелем был написан трактат «Арифметика», в котором он описывал сложение, вычитание, умножение и деление чисел, а также решение уравнений. Он также предложил метод вычисления квадратного корня и извлечения кубического корня.

В 7 веке до нашей эры монументальное произведение «Брахмасфута-сиддханта» индийского математика Бхаскарыачарьи было написано. В этом труде описываются различные арифметические операции, включая возведение в степень, извлечение квадратного и кубического корня, а также решение уравнений.

В 12 веке индийский математик Бхаскарачарья написал «Лилавати», которая стала одной из самых известных индийских книг по математике. В этой книге содержатся различные математические темы, включая арифметику, геометрию и алгебру.

Помимо этих основных текстов, в Древней Индии было развито множество других математических трактатов, которые содержали в себе различные теоремы, формулы и методы решения задач.

История развития математики в Древней Индии является важной частью истории мировой математики и доказывает вклад индийских ученых в развитие этой науки.

Видео по теме:

Вклад индийских математиков в алгебру и арифметику

Математика в Древней Индии была высоко развита, и индийские математики сделали значительный вклад в область алгебры и арифметики.

Одним из самых известных индийских математиков был Арьябхата. В своем трактате «Арьябхатия» он представил новые методы решения уравнений, включая линейные и квадратные уравнения. Арьябхата также ввел символы для обозначения чисел и предложил систему счисления с нулем. Эти идеи были революционными и оказали большое влияние на развитие алгебры.

Еще один важный вклад индийских математиков в алгебру и арифметику был сделан в работе «Лилавати» Бхаскары. Он развил методы решения квадратных уравнений и предложил формулы для вычисления площади треугольника и объема сферы.

Кроме того, индийские математики разработали сложные методы для решения арифметических задач. Например, в «Сиддханта Ширам» Шридхары была предложена формула для нахождения квадратного корня числа. Это было важным достижением, так как ранее не было такого метода для получения точного значения корня.

Таким образом, вклад индийских математиков в алгебру и арифметику был значительным. Их открытия и методы решения уравнений стали основой для развития математики в Древней Индии и оказали влияние на европейскую математику.

Достижения в области чисел и системы счисления

Древняя Индия сделала значительные достижения в области чисел и системы счисления. Одним из самых значимых достижений было введение десятичной системы счисления, которая позже стала широко используемой во всем мире.

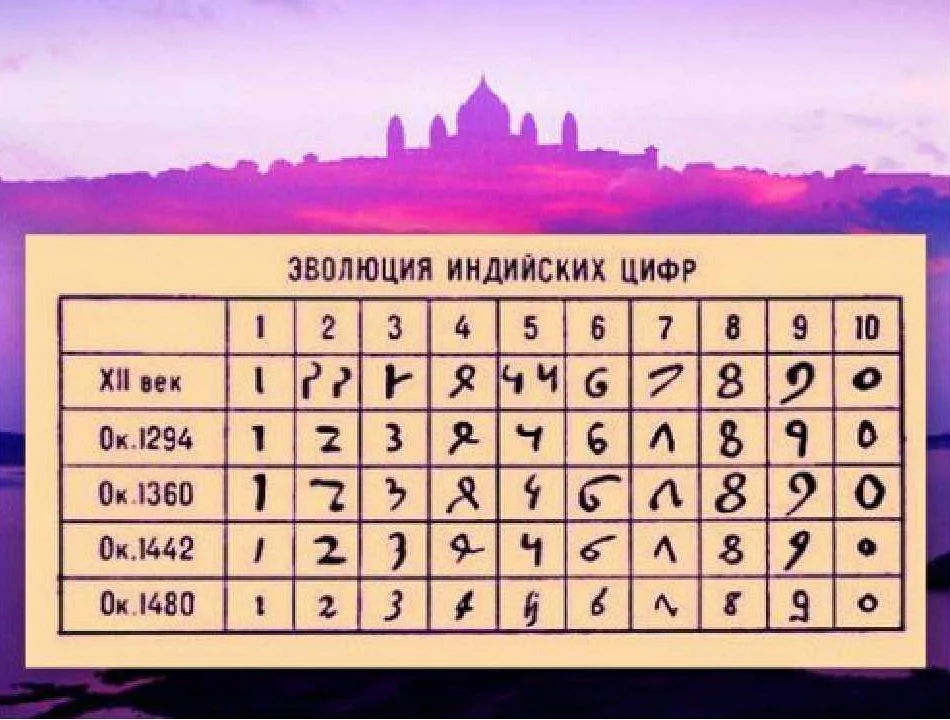
В древнеиндийской математике использовались символы для обозначения чисел, которые были очень похожи на современные цифры. Они использовали символы от 1 до 9 и символ 0, который был представлен как пустое место. Эта система счисления была очень удобна для выполнения арифметических операций и решения математических задач.

Древнеиндийские математики также разработали методы для выполнения сложения, вычитания, умножения и деления с использованием десятичной системы счисления. Они использовали различные алгоритмы и методы, которые позволяли им решать сложные математические задачи эффективно и точно.

Важным достижением было также развитие понятия нуля и его использование в арифметических операциях. Нуль был представлен как символ, который обозначал отсутствие какого-либо значения. Внедрение нуля в систему счисления и его использование в математике было революционным достижением и сыграло важную роль в развитии алгебры и других математических наук.

Древнеиндийская математика также имела высокую степень точности и точности в измерениях и расчетах. Они разработали методы для измерения времени, длины, веса и других величин. Эти методы были использованы в торговле, астрономии и других областях исследований.

В целом, достижения в области чисел и системы счисления в древней Индии были важными и оказали влияние на развитие мировой математики и науки. Их система счисления и методы решения математических задач стали основой для развития современной математики и алгебры.

Вопрос-ответ:

Какие достижения в математике были в Древней Индии?

В Древней Индии были достигнуты значительные успехи в математике. К примеру, были разработаны методы для решения квадратных уравнений, систем линейных уравнений и нахождения корней. Также была создана система записи чисел, которая стала основой для современной десятичной системы счисления.

Какие методы использовались для решения квадратных уравнений в Древней Индии?

Древние индийские математики использовали метод, называемый «формулами Брахмагупты». Этот метод позволял находить корни квадратного уравнения путем применения специальных формул, основанных на коэффициентах уравнения. Также они использовали геометрические методы для решения квадратных уравнений.

Какие проблемы решались системами линейных уравнений в Древней Индии?

Системы линейных уравнений в Древней Индии использовались для решения различных задач. Например, они помогали рассчитывать площади земельных участков, определять объемы жидкостей или смешивать различные виды металлов для создания сплавов. Также системы линейных уравнений использовались для решения задачи о разделении наследства.

Как в Древней Индии записывали числа?

В Древней Индии числа записывались с помощью специальных символов, называемых «цифрами». Они использовали систему позиционного десятичного счисления, которая стала основой для современной системы записи чисел. В этой системе каждая позиция числа имеет свою весовую ценность, и числа записываются путем комбинирования различных цифр.

Какое значение имеет математика в Древней Индии для современности?

Математика в Древней Индии имеет большое значение для современности. Многие методы и достижения, разработанные древними индийскими математиками, стали основой для современной математики. Например, десятичная система счисления и методы решения уравнений, разработанные в Древней Индии, широко применяются в настоящее время. Кроме того, изучение древнеиндийской математики помогает нам лучше понять историю и развитие математической науки.

Какая роль математики играла в Древней Индии?

Математика имела огромное значение в Древней Индии. Она использовалась для решения различных практических задач, таких как расчеты в сельском хозяйстве, строительстве и торговле. Кроме того, математика являлась частью образования брахманов, высшего касты в индийской иерархии. Она была также связана с религиозными и философскими учениями и использовалась для изучения астрологии и астрономии.

Какие достижения в математике были сделаны в Древней Индии?

В Древней Индии были сделаны значительные достижения в математике. Одним из наиболее важных вкладов была разработка десятичной системы счисления, которая является основой для современной математики. Древние индусы также разработали символ нуля и отрицательные числа. Они применяли алгебру для решения линейных и квадратных уравнений, а также разработали методы нахождения квадратных корней и извлечения кубических корней. Кроме того, индийские математики создали различные методы для решения геометрических задач и разработали теоремы о треугольниках и кругах.

Открытие нуля и его значение в математике

Индийские математики первыми в истории открыли и ввели в использование символ для нуля. Раньше в математике не было такого числа, и отсутствие его затрудняло многие вычисления и операции. Открытие нуля позволило значительно упростить математические вычисления и открыть новые горизонты в развитии науки.

Нуль имеет особое значение в различных областях математики. В алгебре, например, ноль является нейтральным элементом для сложения и умножения. В теории чисел ноль играет важную роль при работе с делением и делимостью чисел. Кроме того, нуль является основой системы счисления и позволяет представлять числа в позиционной форме.

Открытие нуля было одним из ключевых шагов в развитии математики и способствовало дальнейшему прогрессу в этой области. Оно позволило сделать сложные вычисления более доступными и точными, открыв новые возможности для решения математических задач и развития научных теорий. Без нуля современная математика была бы немыслима.

Применение математики в астрономии и астрологии

В Древней Индии математика играла важную роль в астрономии и астрологии. Знание математики позволяло астрономам и астрологам проводить сложные расчеты, предсказывать движение планет и звезд, определять времена года и даты праздников.

Астрономия и астрология тесно связаны с математикой, так как для изучения небесных тел необходимо использовать различные математические методы и формулы. В Древней Индии были разработаны различные математические теории и алгоритмы, которые использовались астрономами и астрологами.

Одной из важных областей применения математики было определение движения планет. Индийские астрономы использовали сложные математические модели, чтобы предсказывать положение планет в различные моменты времени. Они разработали методы для вычисления орбит планет и определения их скорости.

Также математика была неотъемлемой частью астрологии в Древней Индии. Астрологи использовали математические методы для составления гороскопов и предсказания событий на основе положения планет в момент рождения человека. Они использовали сложные математические формулы и таблицы для расчетов.

Использование математики в астрономии и астрологии позволяло древнеиндийским ученым проводить точные наблюдения и делать предсказания с высокой степенью точности. Это было важным достижением, которое привело к развитию и распространению астрономии и астрологии в Древней Индии.

Развитие геометрии и тригонометрии в Древней Индии

Древняя Индия оказала значительное влияние на развитие геометрии и тригонометрии. Великий индийский математик Брахмагупта в своем труде «Брахмасфутасиддханта» в 7 веке н.э. впервые представил систему чисел, которая включала отрицательные и десятичные числа, а также ноль. Это было важным достижением, которое положило основу для развития алгебры и геометрии.

Геометрия в Древней Индии была разделена на две главные области: бхуваджа (геометрия земли) и кхетрапатти (геометрия полей). Брахмагупта также представил формулу для вычисления площади треугольника по длинам его сторон — известную как формула Герона. Он также разработал методы для вычисления площади и объема простых и сложных фигур, а также для решения проблем, связанных с теоремой Пифагора.

Тригонометрия в Древней Индии была разработана во время Гуптовской династии (4-6 века н.э.) и основана на работах математика Арьябхатты. Арьябхатта в своем труде «Арьябхаттия» ввел тригонометрические функции, которые были использованы для решения геометрических проблем, включая вычисление длины сторон треугольника и угловых величин.

МатематикДостижения

Брахмагупта	Разработка алгебры и геометрии, формула Герона
Арьябхатта	Введение тригонометрических функций, решение геометрических проблем

Развитие геометрии и тригонометрии в Древней Индии имело огромное значение для развития науки и математики в целом. Открытия и достижения этих индийских математиков оказали влияние на дальнейшее развитие математики в других частях мира.

Методы решения квадратных уравнений и систем уравнений

Метод Брахмагупты основан на выведении формулы для нахождения корней квадратного уравнения вида ax^2 + bx + c = 0, где a, b и c — коэффициенты, причем a ≠ 0. Для нахождения корней уравнения используется формула:

x = (-b ± √(b^2 — 4ac)) / (2a).

Брахмагупта также разработал метод решения системы квадратных уравнений с двумя неизвестными. Он предложил выразить одну переменную через другую в одном уравнении и подставить это выражение во второе уравнение, получив таким образом одно уравнение с одной неизвестной. Затем это уравнение решается методом Брахмагупты для квадратных уравнений.

Другой метод решения квадратных уравнений, применяемый в Древней Индии, называется методом Шридхары. Он основан на завершении квадратного трехчлена до полного квадрата. Для этого трехчлен представляется в виде суммы двух квадратов и затем производится факторизация.

Метод Шридхары также может быть применен для решения системы уравнений с двумя неизвестными. В этом случае каждое уравнение системы приводится к виду квадратного трехчлена, который затем завершается до полного квадрата. Полученные уравнения суммируются и факторизуются, что позволяет найти значения неизвестных.

Оба метода, предложенные Брахмагуптой и Шридхарой, были важными достижениями в развитии математики в Древней Индии. Они позволяли решать квадратные уравнения и системы уравнений быстро и эффективно, что имело применение не только в математических вычислениях, но также в астрономии, архитектуре и других практических областях.

МетодОписание

Метод Брахмагупты	Нахождение корней квадратного уравнения через формулу
Метод Шридхары	Завершение квадратного трехчлена до полного квадрата

Особенности математического образования в Древней Индии

Математика в Древней Индии имела свои особенности, которые отличали ее от математических традиций других древних цивилизаций. Одной из главных особенностей была использование символов и системы численной записи, которая была разработана индийскими математиками.

В Древней Индии была развита десятичная система с позиционным обозначением чисел, где каждый символ имеет свое значение в зависимости от его позиции. Эта система использовала символы от 0 до 9, которые позволяли записывать числа любой величины. Индийские математики также ввели символ нуля, что является важным достижением в истории математики.

Еще одной особенностью математического образования в Древней Индии было введение алгебраических методов решения уравнений. Индийские математики разработали методы решения линейных и квадратных уравнений, а также систем уравнений. Они использовали символы и обозначения, чтобы представить уравнения и решать их с помощью алгебраических операций.

Кроме того, математика в Древней Индии была тесно связана с астрономией. Индийские математики разработали методы для измерения времени, определения календарей и прогнозирования астрономических событий. Они использовали геометрию и тригонометрию для изучения движения небесных тел и разработки астрономических таблиц.

В результате этих особенностей математического образования в Древней Индии, индийские математики сделали значительные вклады в развитие математики в целом. Их работы и методы использовались и развивались впоследствии другими культурами, включая арабскую и европейскую математику.