Что такое неравенство в математике 1 класс примеры и решения

Неравенство в математике для учеников 1 класса – это понятие, которое объясняет отношение между числами и знаками больше, меньше и равно. В данной статье вы найдете примеры и решения задач на неравенство для первоклассников. Познакомьтесь с основными правилами и методами решения неравенств и помогите своему ребенку легко освоить этот важный математический концепт.

Математика — это один из основных предметов, которым занимаются ученики начальной школы. Уже с первого класса дети начинают изучать основные математические понятия и операции. Одним из таких понятий являются неравенства.

Неравенства — это математические выражения, которые показывают, какие числа больше или меньше других. Они помогают ученикам развивать логическое мышление и умение сравнивать числа. Неравенства записываются с помощью знаков «больше» (>) и «меньше» (

Примеры неравенств могут выглядеть следующим образом: 2 > 1, 5 < 10, 9 > 5. В этих примерах первое число справа от знака неравенства больше второго числа слева от знака неравенства. Такие неравенства можно решать, сравнивая числа и приходя к правильному ответу.

Например, если у нас есть неравенство 8 > 3, то мы можем сказать, что число 8 больше числа 3.

Все эти навыки помогут ученикам не только в математике, но и в повседневной жизни. Знание неравенств позволит им сравнивать разные объекты, объемы и т.д. и принимать обоснованные решения.

Что такое неравенства в математике?

Неравенства включают знаки сравнения, такие как «больше» (>), «меньше» (

Неравенства могут использоваться для решения различных задач, например, для определения диапазона возможных значений переменных или для сравнения результатов различных выражений.

В математике для 1 класса неравенства используются для введения понятий «больше» и «меньше» и развития навыков сравнения чисел. Например, ребенку могут предлагать сравнить количество фруктов на двух картинках и записать соответствующее неравенство.

Определение и основные понятия

Неравенства полезно использовать для сравнения чисел и выражений. Например, если у нас есть два числа — 5 и 7, то мы можем записать неравенство «5 < 7», что означает, что число 5 меньше числа 7.

Для решения неравенств используются различные методы, включая перенос чисел из одной стороны неравенства в другую, а также применение операций сложения, вычитания, умножения и деления.

Неравенства помогают нам лучше понимать отношение между числами и решать различные задачи, связанные с сравнением и порядком чисел.

Примеры неравенств в математике

Примеры неравенств:

1. 2 < 5 — это неравенство говорит нам, что число 2 меньше числа 5.

2. 7 > 3 — это неравенство говорит нам, что число 7 больше числа 3.

3. 4 ≤ 4 — это неравенство говорит нам, что число 4 меньше или равно числу 4.

4. 6 ≥ 2 — это неравенство говорит нам, что число 6 больше или равно числу 2.

Обратите внимание, что символы «» (больше), «≤» (меньше или равно) и «≥» (больше или равно) используются для обозначения неравенств в математике.

Неравенства позволяют нам сравнивать числа и выражения и решать различные задачи. Они широко применяются в алгебре, геометрии и других областях математики.

Как решать неравенства в математике?

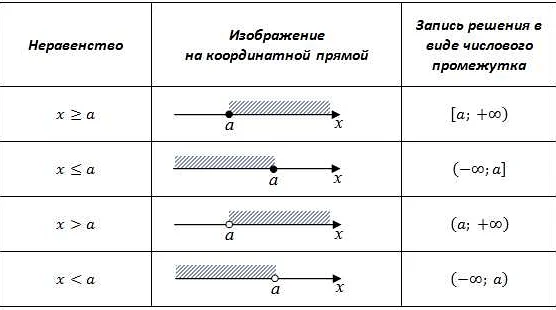
Для решения неравенств нужно учитывать следующие правила:

1. Если в неравенстве стоит знак «
2. Если в неравенстве стоит знак «>», то нужно найти наименьшее значение, которое может принимать переменная, чтобы неравенство было верным. Например, если задано неравенство x > 3, то наименьшее значение переменной x будет 4.
3. Если в неравенстве стоит знак «
4. Если в неравенстве стоит знак «>=», то нужно найти наименьшее значение, которое может принимать переменная, чтобы неравенство было верным. Например, если задано неравенство x >= 6, то наименьшее значение переменной x будет 6.

При решении неравенств также необходимо учитывать арифметические операции, которые могут присутствовать в выражениях. Например, при умножении или делении на отрицательное число в неравенстве, необходимо поменять направление знака. Также можно использовать свойства неравенств, например, складывание или вычитание одного и того же числа с обеих сторон неравенства.

Практика и тренировка помогут закрепить навык решения неравенств в математике. Регулярное решение задач и примеров поможет стать более уверенным в этой теме и позволит использовать неравенства в реальных ситуациях.

Методы решения

В математике для решения неравенств используются различные методы. Ниже представлены основные методы решения неравенств в 1 классе.

1. Метод «подставления». При использовании этого метода необходимо подставить значения переменных в неравенство и проверить его истинность. Например, для неравенства «5 + x < 10» можно подставить различные значения переменной x и проверить, выполняется ли неравенство.
2. Метод «переноса». Этот метод заключается в переносе одного из членов неравенства на другую сторону с противоположным знаком. Например, для неравенства «6 — x > 2» можно перенести член «x» на другую сторону, изменяя его знак, и получить «6 — 2 < x».
3. Метод «преобразования». Данный метод заключается в преобразовании неравенства с помощью математических операций. Например, для неравенства «3 * x + 4 < 10» можно вычесть 4 из обеих сторон неравенства и получить «3 * x < 6».

При решении неравенств важно помнить о правилах выполнения математических операций и их влиянии на неравенства. Также следует обращать внимание на знаки неравенства и правильно их использовать при применении методов решения.

Практические примеры решения неравенств

Для лучшего понимания и освоения материала, предлагаем рассмотреть несколько практических примеров решения неравенств.

Пример 1:

НеравенствоРешение

x + 5 < 10

Вычтем 5 из обеих частей неравенства: x < 5

Пример 2:

НеравенствоРешение

2y — 3 > 7	Прибавим 3 к обеим частям неравенства: 2y > 10
	Разделим обе части неравенства на 2: y > 5

Пример 3:

НеравенствоРешение

4z + 2 ≤ 18	Вычтем 2 из обеих частей неравенства: 4z ≤ 16
	Разделим обе части неравенства на 4: z ≤ 4

Примеры решения неравенств помогут вам лучше усвоить правила и применение неравенств в математике. Постепенно, с практикой, вы будете все лучше справляться с данной темой.

Видео по теме:

Вопрос-ответ:

Какие примеры неравенств можно решать в 1 классе?

В 1 классе можно решать примеры неравенств с числами от 1 до 10, например: 3 < 5, 8 > 2 и т.д.

Каким образом можно решить пример «5 > 2»?

Пример «5 > 2» можно решить, сравнивая числа. В данном случае 5 больше 2, поэтому утверждение верно.

Какие знаки используются в неравенствах?

В неравенствах используются следующие знаки: «» (больше) и «=» (больше или равно).

Можно ли решить пример «4 < 2»?

Пример «4 < 2» не имеет решения, потому что 4 не может быть меньше 2. В этом случае утверждение неверно.

Можно ли использовать неравенства в повседневной жизни?

Да, неравенства можно использовать в повседневной жизни для сравнения различных величин, например, при покупке товаров по цене или при определении размеров предметов.

Какие примеры неравенств можно встретить в математике для 1 класса?

В математике для 1 класса можно встретить примеры неравенств, такие как 2 < 5, 7 > 3, 4 + 2 > 5.

Как решить неравенство в математике для 1 класса?

Для решения неравенства в математике для 1 класса нужно сравнить два числа и определить, какое из них больше или меньше. Затем нужно записать знак больше или меньше между числами и решение получится.

Зачем нужно изучать неравенства в математике?

Изучение неравенств развивает навыки логического мышления и алгоритмического мышления учащихся. Эти навыки помогают анализировать и решать сложные задачи, а также применять математические знания в реальной жизни.

Неравенства также играют важную роль в различных областях науки и техники. Они используются в экономике, физике, информатике и других дисциплинах для моделирования и решения различных задач.

Изучение неравенств помогает развивать у учащихся уверенность в себе и способность к решению сложных проблем. Эти навыки будут полезными как в школе, так и в жизни в целом.

Таким образом, изучение неравенств в математике позволяет развивать логическое мышление, применять математические знания на практике и развивать уверенность в себе и способность к решению сложных задач.

Практическое применение неравенств

Например, неравенства могут использоваться для сравнения количества предметов или для определения диапазона чисел. Если у нас есть корзина с яблоками, мы можем использовать неравенства, чтобы определить, сколько яблок в корзине. Например, если в корзине есть больше 5 яблок, мы можем записать неравенство «количество яблок > 5».

Неравенства также могут использоваться для решения задач финансового характера. Например, если у нас есть задача о покупке товаров, мы можем использовать неравенства, чтобы определить, сколько денег мы можем потратить. Например, если у нас есть 1000 рублей, мы можем записать неравенство «деньги >= 1000».

Еще одним примером практического применения неравенств является оценка успехов в учебе. Если ученик получает оценки по предметам, мы можем использовать неравенства, чтобы определить, какие наибольшие и наименьшие оценки он получил. Например, если у него есть две пятерки и одна четверка, мы можем записать неравенство «наибольшая оценка >= 5» и «наименьшая оценка

Таким образом, неравенства имеют широкое применение в реальной жизни и помогают нам решать различные задачи. Изучение неравенств в математике помогает развивать логическое мышление и позволяет применять полученные знания в повседневной жизни.