Профильная математика егэ как оцениваются задания
Содержимое
- 1 Профильная математика егэ как оцениваются задания
- 1.1 Оценка заданий профильной математики ЕГЭ
- 1.2 Основные принципы оценки
- 1.3 Критерии оценки заданий
- 1.4 Оценка заданий на аналитическую геометрию
- 1.5 Оценка заданий на дифференциальное исчисление
- 1.6 Оценка заданий на интегралы
- 1.7 Оценка заданий на теорию вероятностей и математическую статистику
- 1.8 Оценка заданий на математическую логику и алгебру
- 1.9 Вопрос-ответ:
- 1.9.0.1 Какие основные принципы оценки заданий профильной математики ЕГЭ?
- 1.9.0.2 Какие критерии используются при оценке заданий профильной математики ЕГЭ?
- 1.9.0.3 Каким образом происходит оценка заданий профильной математики ЕГЭ?
- 1.9.0.4 Какие принципы оценки заданий профильной математики ЕГЭ являются наиболее важными?
- 1.9.0.5 Какие критерии оценки заданий профильной математики ЕГЭ наиболее важны для получения высокого балла?
- 1.9.0.6 Какие принципы лежат в основе оценки заданий профильной математики ЕГЭ?
- 1.10 Видео по теме:
Узнайте, как оцениваются задания по профильной математике в ЕГЭ. Разберитесь, какая система баллов применяется и как устроены критерии оценки. Подготовьтесь к экзамену основательно, чтобы получить высокий балл.
Оценка заданий профильной математики на ЕГЭ осуществляется в соответствии с определенными принципами и критериями. Эти принципы и критерии устанавливаются для обеспечения объективности и справедливости оценивания.
Один из основных принципов оценки заданий математического профиля — это принцип многоуровневого оценивания. Согласно этому принципу, каждое задание оценивается на нескольких уровнях сложности. Это позволяет ученикам с разным уровнем подготовки получить соответствующую оценку.
Критерии оценивания заданий математического профиля также строго определены. Оценка задания зависит от правильности выполнения и от степени сложности решения. Важным критерием является также ясность и логичность изложения мыслей, а также использование математических терминов и символов.
Оценка заданий профильной математики на ЕГЭ является важным этапом в оценивании математической подготовки выпускников. Она позволяет определить уровень знаний и навыков учеников в данной области и оценить их готовность к дальнейшему образованию и профессиональной деятельности.
В целом, оценка заданий профильной математики на ЕГЭ осуществляется с учетом объективности, справедливости и строго определенных критериев. Это позволяет получить достоверные результаты и составить объективную картину уровня знаний и навыков выпускников в области математики.
Оценка заданий профильной математики ЕГЭ
Оценка заданий профильной математики ЕГЭ осуществляется согласно определенным принципам и критериям. Комиссия, состоящая из опытных экспертов, проводит анализ и оценку каждого задания, чтобы определить его сложность, уровень абстрактности и требуемые знания и навыки ученика.
Оценка заданий профильной математики ЕГЭ основывается на следующих принципах:
- Объективность. Оценивание заданий проводится согласно четко определенным критериям, что позволяет минимизировать субъективность оценки.
- Справедливость. Все ученики оцениваются по одним и тем же критериям, что обеспечивает равные возможности для всех участников экзамена.
- Приближение к реальным задачам. Задания ЕГЭ в профильной математике направлены на проверку практических навыков решения математических проблем, которые могут возникнуть в реальной жизни или будущей профессиональной деятельности ученика.
Для оценки заданий профильной математики ЕГЭ применяются следующие критерии:
- Правильность. Оценивается, насколько точно и корректно ученик решил задание, наличие ошибок и правильность полученного ответа.
- Логическая последовательность решения. Оценивается, насколько ученик последовательно и логично применял математические методы и операции при решении задания.
- Адекватность использованных методов. Оценивается, насколько ученик выбрал и применил подходящие методы и стратегии для решения задачи.
- Полнота и ясность изложения. Оценивается, насколько ученик четко и полно изложил свои мысли и рассуждения при решении задания.
Оценка заданий профильной математики ЕГЭ является важным этапом в процессе проведения экзамена и позволяет объективно оценить знания и умения ученика в данной области математики.
Основные принципы оценки
Оценка заданий профильной математики ЕГЭ основывается на ряде принципов, которые определяют правила и критерии оценивания работ учащихся. Эти принципы обеспечивают объективность и справедливость процесса оценки, позволяя достоверно определить уровень знаний и умений учеников.
Первым принципом оценки является строгое соблюдение критериев, которые установлены для каждого задания. Каждое задание имеет определенные правила выполнения и способы решения, которые должны быть учтены при оценивании. Это позволяет обеспечить объективность и одинаковые условия для всех участников экзамена.
Вторым принципом является четкость и ясность формулировки критериев оценивания. Критерии должны быть понятными и однозначными, чтобы оценщики могли корректно оценить работу ученика. Также важно, чтобы оценщики были владельцами необходимых знаний и опыта для правильного толкования критериев.
Третий принцип — это честность и независимость оценки. Оценщики должны быть независимыми и не иметь предвзятости по отношению к ученикам. Они должны строго придерживаться установленных критериев и не допускать субъективных суждений при оценивании. Это помогает обеспечить справедливость процесса оценки.
Четвертый принцип — это дифференциация оценки. Оценивание должно позволять выделить разные уровни знаний и умений учащихся. Для этого используются шкалы оценок, которые позволяют разделить учеников на группы в зависимости от их результатов. Это позволяет более точно определить уровень подготовки каждого участника экзамена.
И, наконец, пятый принцип — это обратная связь. Оценка должна предоставлять ученикам информацию о качестве их работы. Это помогает им понять свои ошибки и недочеты, а также улучшить свои навыки и знания в будущем.
Критерии оценки заданий
При оценке заданий по профильной математике ЕГЭ применяются определенные критерии, которые позволяют выставить соответствующую оценку за выполнение задания. Критерии оценки позволяют учащимся понять, какие требования должны быть выполнены, чтобы получить максимальное количество баллов за задание.
Основные критерии оценки заданий по профильной математике включают:
КритерийОписание
| Правильность решения | Оценивается правильность математического решения задачи, соответствие полученного результата правильному ответу. |
| Логическая последовательность | Оценивается логичность и последовательность рассуждений, использование корректных математических операций и методов. |
| Аргументация и обоснование | Оценивается умение обосновывать принятые решения, объяснять выбранные методы и стратегии решения задачи. |
| Точность и аккуратность | Оценивается точность и аккуратность выполнения вычислений и промежуточных шагов решения задачи. |
| Соблюдение условий задачи | Оценивается соблюдение условий задачи, правильность интерпретации и применение данных, указанных в условии задачи. |
Каждый критерий оценки имеет свой вес, который определяет вклад критерия в общую оценку задания. Применение критериев оценки позволяет объективно оценить выполнение задания и выставить соответствующую оценку в соответствии с заданными критериями.
Оценка заданий на аналитическую геометрию
Оценка заданий на аналитическую геометрию включает в себя ряд основных принципов и критериев, которые помогают определить достоверность и точность решений. Эти принципы и критерии позволяют оценить уровень математической подготовки учащихся, их понимание основных понятий и методов аналитической геометрии, а также умение применять их на практике.
Одним из основных критериев оценки заданий на аналитическую геометрию является точность решения. Учащиеся должны показать, что они способны правильно применять формулы и методы аналитической геометрии, а также проводить вычисления без ошибок. Точность выполнения всех вычислений и преобразований является одним из важных условий получения положительной оценки.
Кроме того, важным критерием оценки является логичность решения. Учащиеся должны показать, что они способны аргументированно и последовательно проводить логические рассуждения, объяснять свои действия и выводы. Логичность решения позволяет определить, насколько точно учащийся понимает поставленную задачу и умеет анализировать информацию, представленную в условии задачи.
Еще одним критерием оценки заданий на аналитическую геометрию является оформление решения. Учащиеся должны показать, что они способны ясно, четко и аккуратно излагать свои мысли, представлять решение в понятном виде. Оформление решения включает в себя правильное использование математических обозначений, графиков, таблиц и других вспомогательных средств, которые помогают наглядно представить решение задачи.
Таким образом, оценка заданий на аналитическую геометрию основывается на оценке точности решения, логичности рассуждений и оформления решения. Учащиеся должны продемонстрировать свои знания и умения в области аналитической геометрии, а также показать, что они способны применять их на практике. Выполнение всех этих критериев является основным условием получения высокой оценки на заданиях по аналитической геометрии ЕГЭ.
Оценка заданий на дифференциальное исчисление

При оценке заданий на дифференциальное исчисление важно учитывать следующие критерии:
- Корректность и точность решения. Учащийся должен правильно применить основные правила дифференцирования, учесть все условия задачи и правильно произвести вычисления. Ошибки, допущенные при вычислениях, могут привести к снижению баллов.
- Ясность и полнота изложения. Учащийся должен четко и ясно изложить свои мысли, объяснить каждый шаг решения и использовать точные математические обозначения. Неясное изложение или неполные объяснения могут привести к потере баллов.
- Логичность и последовательность рассуждений. Учащийся должен последовательно и логично излагать свои мысли, объяснять свои действия и выводы. Нелогичные или противоречивые рассуждения могут привести к снижению баллов.
- Самостоятельность и творческий подход. Оцениваются не только правильные ответы, но и способность учащегося самостоятельно мыслить, применять знания и навыки в нестандартных ситуациях. Творческий подход и оригинальные решения могут быть оценены выше.
При оценке заданий также учитывается сложность задачи, ее взаимосвязь с другими темами и возможность применения различных методов и подходов. Оценка проводится с учетом всех этих факторов и принципов, и помогает определить уровень подготовки учащегося в области дифференциального исчисления.
Оценка заданий на интегралы
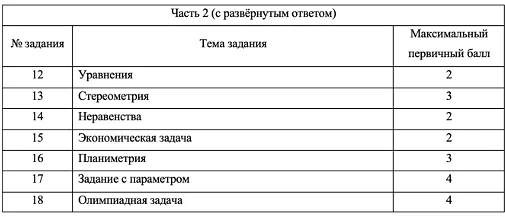
Оценка заданий на интегралы в профильной математике ЕГЭ основывается на нескольких принципах и критериях. Задания на интегралы проверяют умение учащихся решать задачи, связанные с определенными функциями и их интегралами.
Основной критерий оценки заданий на интегралы — это правильность решения задачи. Учащийся должен правильно определить заданные пределы интегрирования, выбрать подходящую для решения функцию и выполнить все необходимые алгебраические преобразования для получения правильного ответа.
Кроме того, оценка заданий на интегралы также основывается на понимании учащимися основных свойств и формул интегралов. Они должны знать основные формулы для интегрирования различных типов функций, таких как степенные функции, тригонометрические функции и экспоненциальные функции.
Также важным критерием оценки заданий на интегралы является точность и строгость в выполнении математических операций. Учащийся должен представлять свои решения в форме, которая позволяет легко проверить каждый шаг и убедиться в его правильности.
И наконец, оценка заданий на интегралы также учитывает способность учащихся анализировать и интерпретировать результаты. Они должны понимать значение интеграла в контексте задачи и уметь объяснить его физический или геометрический смысл.
КритерийОписание
| Правильность решения | Учащийся должен правильно определить пределы интегрирования, выбрать подходящую функцию и выполнить все необходимые алгебраические преобразования для получения правильного ответа. |
| Знание основных формул и свойств интегралов | Учащиеся должны знать основные формулы для интегрирования различных типов функций, таких как степенные функции, тригонометрические функции и экспоненциальные функции. |
| Точность и строгость математических операций | Учащийся должен представлять свои решения в форме, которая позволяет легко проверить каждый шаг и убедиться в его правильности. |
| Анализ и интерпретация результатов | Учащиеся должны понимать значение интеграла в контексте задачи и уметь объяснить его физический или геометрический смысл. |
Оценка заданий на теорию вероятностей и математическую статистику
Оценка заданий на теорию вероятностей и математическую статистику в контексте ЕГЭ по профильной математике основывается на нескольких принципах и критериях.
Во-первых, при оценке заданий учитывается корректность математического решения. Это означает, что ученик должен правильно применить теоретические знания и методы решения задач, связанных с теорией вероятностей и математической статистикой. Важно также показать все промежуточные вычисления и логические шаги, чтобы проверяющий мог убедиться в правильности решения.
Во-вторых, при оценке заданий учитывается логичность и последовательность аргументации. Ученик должен четко объяснить каждый шаг своего решения и продемонстрировать связь между различными элементами задачи. Важно, чтобы решение задачи было представлено в логической и последовательной форме, позволяющей проверяющему легко следовать логике решения.
В-третьих, при оценке заданий учитывается точность ответа. В контексте заданий на теорию вероятностей и математическую статистику точность ответа играет важную роль, поскольку малейшая ошибка в вычислениях или неправильное округление может привести к неправильному ответу. Проверяющий обращает внимание на десятичные знаки и их округление, чтобы определить точность ответа.
Наконец, при оценке заданий учитывается полнота и адекватность ответа. Ученик должен полностью ответить на поставленный в задании вопрос, а также дать все необходимые объяснения и доказательства. Важно также, чтобы ответ был представлен в форме, понятной и корректной для предметной области теории вероятностей и математической статистики.
Все эти принципы и критерии оценки заданий на теорию вероятностей и математическую статистику помогают проверяющим оценить уровень подготовки ученика в этих областях и дать объективную оценку его знаний и навыков.
Оценка заданий на математическую логику и алгебру
Оценка заданий на математическую логику и алгебру включает в себя оценку умения учащихся применять логические рассуждения и алгебраические методы решения задач. Данный раздел математического ЕГЭ проверяет навыки анализа, логического мышления и решения сложных алгебраических уравнений.
Оценка заданий на математическую логику и алгебру основывается на нескольких критериях:
- Правильность решения задачи. Оценка основывается на правильности применения логических операций и алгебраических методов для решения задачи. Необходимо доказать правильность всех этапов решения и получить верный ответ.
- Логическая последовательность решения. Оценка основывается на логической последовательности решения задачи. Учащийся должен показать четкую цепочку логических рассуждений, следовать последовательности действий и объяснить каждый шаг.
- Точность и ясность изложения. Оценка основывается на ясности и точности изложения решения задачи. Учащийся должен четко и понятно изложить свои мысли, использовать правильные математические обозначения и термины.
- Корректность использования математических методов. Оценка основывается на корректности использования математических методов при решении задачи. Учащийся должен правильно применять алгебраические методы, формулы и свойства для получения правильных ответов.
- Обоснованность ответа. Оценка основывается на обоснованности ответа. Учащийся должен объяснить, почему его ответ является правильным, представить доказательство или логическое обоснование своего решения.
Каждый из этих критериев влияет на оценку задания по математической логике и алгебре. Оценка может быть выставлена с учетом всех критериев или только по одному из них, в зависимости от типа задания и поставленных требований.
Вопрос-ответ:
Какие основные принципы оценки заданий профильной математики ЕГЭ?
Основные принципы оценки заданий профильной математики ЕГЭ включают объективность, надежность и согласованность. Объективность подразумевает, что оценка заданий должна быть независима от личных предпочтений эксперта. Надежность означает, что результаты оценки должны быть стабильными и повторяемыми. А согласованность требует, чтобы оценка заданий была согласована с общими принципами оценки ЕГЭ.
Какие критерии используются при оценке заданий профильной математики ЕГЭ?
При оценке заданий профильной математики ЕГЭ используются следующие критерии: полнота выполнения задания, правильность решения, математическая точность, логичность и четкость изложения решения, использование математических понятий, обозначений и символов.
Каким образом происходит оценка заданий профильной математики ЕГЭ?
Оценка заданий профильной математики ЕГЭ происходит путем применения критериев оценки к каждому заданию. Эксперты сравнивают решения учащихся с эталонными и оценивают их согласно предложенным критериям. Затем результаты оценки суммируются и преобразуются в баллы, которые затем учитываются при выставлении итоговой оценки за экзамен.
Какие принципы оценки заданий профильной математики ЕГЭ являются наиболее важными?
Все принципы оценки заданий профильной математики ЕГЭ являются важными, но можно выделить два основных: объективность и надежность. Объективность гарантирует, что оценка заданий будет справедливой и не будет зависеть от личных предпочтений эксперта. А надежность обеспечивает стабильность и повторяемость результатов оценки.
Какие критерии оценки заданий профильной математики ЕГЭ наиболее важны для получения высокого балла?
Для получения высокого балла по заданиям профильной математики ЕГЭ важно учесть все критерии оценки и выполнить задание полностью и правильно. Особое внимание следует уделить правильности решения, математической точности и логичности изложения, а также использованию математических понятий, обозначений и символов.
Какие принципы лежат в основе оценки заданий профильной математики ЕГЭ?
Основными принципами оценки заданий профильной математики ЕГЭ являются объективность, надежность и стандартизация. Объективность означает, что оценка заданий основывается на четких и однозначных критериях, а не на субъективном мнении проверяющих. Надежность подразумевает, что результаты оценки должны быть стабильными и не зависеть от случайных факторов. Стандартизация предполагает, что процесс оценки должен быть единообразным для всех участников ЕГЭ.

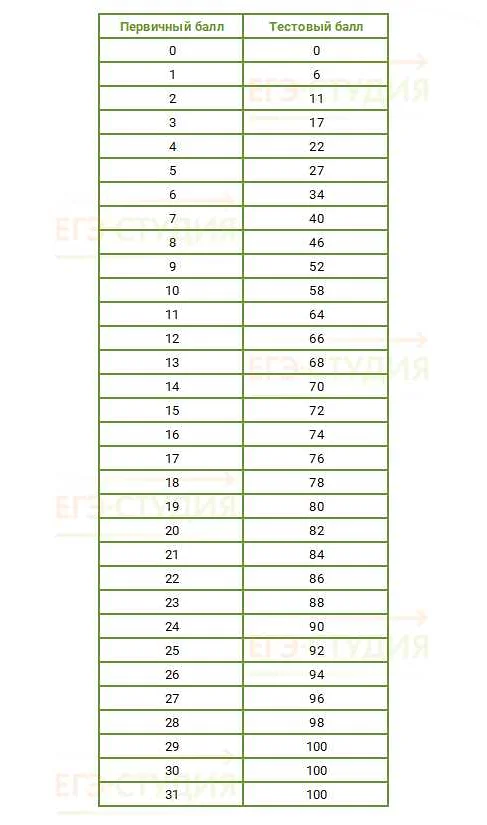
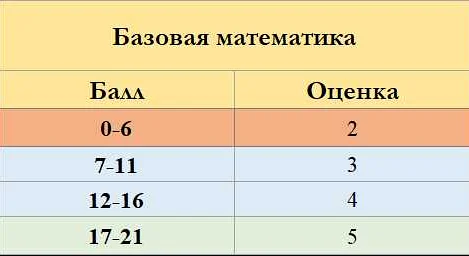

Статья очень интересная и полезная! В ней я нашел много полезной информации о процессе оценки заданий по математике на ЕГЭ. Основные принципы и критерии, которые используют эксперты при оценке работ, были подробно рассмотрены. Было очень интересно узнать, что оценивание заданий основывается на объективных критериях, что делает процесс более справедливым. Я также узнал, что эксперты при оценке заданий акцентируют внимание на процессе решения, а не только на правильности ответа. Это очень важно, потому что таким образом проявляется уровень понимания математических концепций у выпускников. Я узнал много нового и полезного из статьи, и теперь лучше понимаю, как именно оцениваются задания по математике на ЕГЭ. Спасибо за интересную статью!