Огэ по математике 2022 формулы которые даны

В статье представлены формулы, которые даны на ОГЭ по математике в 2022 году. Здесь вы найдете все необходимые формулы и правила для успешной подготовки к экзамену. Используйте эту информацию, чтобы уверенно справиться с заданиями на ОГЭ по математике.

Ежегодно множество выпускников 9 классов готовится к сдаче ОГЭ по математике. Для успешного прохождения экзамена необходимо усвоить определенный набор математических формул, которые используются в различных задачах. Опытные преподаватели и эксперты рекомендуют уделить особое внимание изучению этих формул, чтобы быть готовым к любому заданию.

Перечень формул, которые нужно знать, включает в себя различные области математики, такие как алгебра, геометрия и вероятность. Например, необходимо знать формулы для решения уравнений, систем уравнений, построения графиков функций и вычисления площади и объема геометрических фигур.

Важно отметить, что формулы необходимо не только знать, но и уметь применять в практических задачах. Поэтому рекомендуется регулярно решать разнообразные задачи, чтобы набраться опыта и уверенности в использовании формул.

Запомните, что ОГЭ по математике — это не только проверка знания формул, но и умение анализировать задачи, применять логическое мышление и находить решения. Поэтому не забывайте тренироваться на разные типы задач, чтобы быть готовыми к экзамену.

Общая информация

Экзамен состоит из двух частей: письменной и устной. Письменная часть включает в себя решение задач различного уровня сложности. Устная часть представляет собой собеседование с учеником, во время которого задаются вопросы на проверку понимания математических концепций.

На ОГЭ по математике учащиеся должны знать основные математические формулы и уметь применять их в решении задач. Формулы могут относиться к разным областям математики, таким как геометрия, алгебра, тригонометрия и т.д.

Правильная подготовка к ОГЭ по математике включает изучение всех необходимых формул и их применение на практике. Это поможет ученикам повысить свой уровень знаний и уверенность в себе перед экзаменом.

Структура ОГЭ по математике

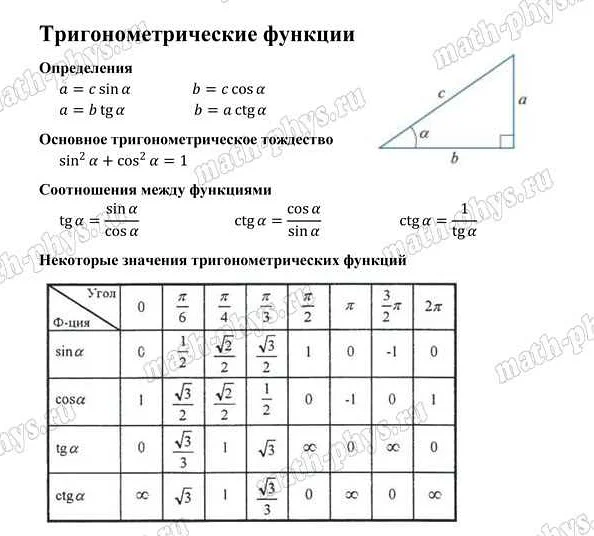
ОГЭ по математике состоит из двух частей: первой и второй. Обе части имеют одинаковое количество заданий (15) и оцениваются по 10-балльной шкале.

Первая часть ОГЭ по математике включает в себя задания, проверяющие знание основ математики и базовых навыков решения простых задач. Здесь могут быть представлены задания на арифметические действия, работу с дробями, процентами, десятичными дробями, а также на измерение длины, площади и объема. В первой части также могут быть задания, связанные с графиками и таблицами данных.

Вторая часть ОГЭ по математике состоит из заданий, проверяющих умение применять изученные математические понятия и методы для решения сложных задач. Здесь могут быть представлены задания на решение уравнений и неравенств, работу с геометрическими фигурами, построение графиков функций, анализ статистических данных и многое другое.

Обе части ОГЭ по математике рассчитаны на выполнение за ограниченное время. Время на выполнение первой части составляет 45 минут, на выполнение второй части — 90 минут. Перерыв между частями составляет 20 минут.

ЧастьКоличество заданийВремя на выполнение

Первая	15	45 минут
Вторая	15	90 минут

Формулы для работы с числами

Формула сложения: сумма двух чисел a и b равна их сумме: a + b.

Формула вычитания: разность двух чисел a и b равна их разности: a — b.

Формула умножения: произведение двух чисел a и b равно их умножению: a × b.

Формула деления: частное от деления числа a на число b равно их отношению: a ÷ b.

Формула возведения в степень: a в степени n равно произведению числа a на себя n раз: an.

Формула извлечения корня: корень степени n из числа a равен числу b, такому что b в степени n равно числу a: √an = b.

Формула процента: число x процентов от числа y равно произведению числа y на десятичную дробь, равную x/100: x% от y = (x/100) × y.

Формула пропорции: в пропорции a:b = c:d отношение a к b равно отношению c к d: a/b = c/d.

Формула среднего арифметического: среднее арифметическое нескольких чисел равно их сумме, деленной на их количество: СА = (a1 + a2 + … + an) / n.

Формула среднего геометрического: среднее геометрическое нескольких чисел равно корню из их произведения: СГ = √(a1 × a2 × … × an).

Формула среднего квадратического: среднее квадратическое нескольких чисел равно корню из их суммы квадратов, деленной на их количество: СК = √((a1² + a2² + … + an²) / n).

Формула бинома Ньютона: разложение бинома (a + b)n в сумму слагаемых можно получить с помощью формулы: (a + b)n = C(n, 0) × an × b0 + C(n, 1) × an-1 × b1 + … + C(n, n) × a0 × bn, где C(n, k) — число сочетаний из n элементов по k.

Геометрические формулы

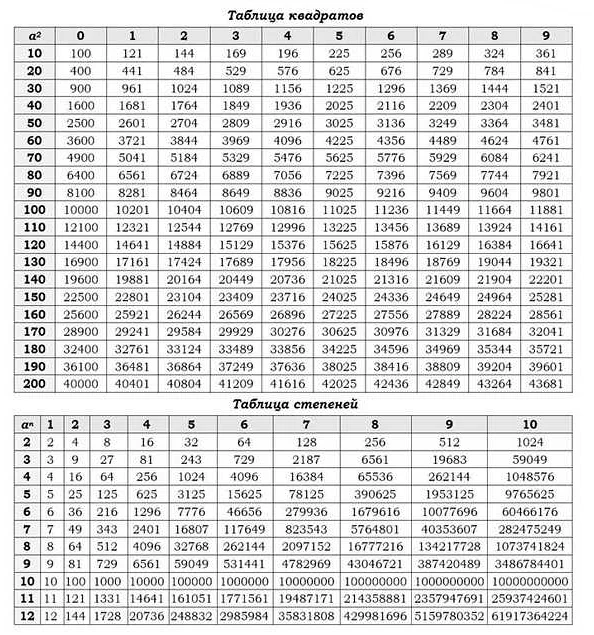
В математике и геометрии существует множество формул, которые помогают решать различные задачи. Они основаны на свойствах геометрических фигур и объектов.

Формулы для вычисления площадей:

Площадь прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.

Площадь квадрата: S = a * a, где a — длина стороны квадрата.

Площадь треугольника: S = (a * h) / 2, где a — длина основания треугольника, h — высота треугольника, проведенная к основанию.

Площадь круга: S = π * r^2, где π — математическая константа, равная примерно 3.14, r — радиус круга.

Формулы для вычисления объемов:

Объем прямоугольного параллелепипеда: V = a * b * h, где a, b и h — длины сторон прямоугольного параллелепипеда.

Объем куба: V = a * a * a, где a — длина стороны куба.

Объем цилиндра: V = π * r^2 * h, где π — математическая константа, равная примерно 3.14, r — радиус основания цилиндра, h — высота цилиндра.

Объем шара: V = (4/3) * π * r^3, где π — математическая константа, равная примерно 3.14, r — радиус шара.

Формулы для вычисления длин:

Длина окружности: L = 2 * π * r, где π — математическая константа, равная примерно 3.14, r — радиус окружности.

Длина отрезка на плоскости: L = √((x2 — x1)^2 + (y2 — y1)^2), где (x1, y1) и (x2, y2) — координаты концов отрезка на плоскости.

Формула для вычисления теоремы Пифагора:

Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. a^2 + b^2 = c^2, где a и b — длины катетов, c — длина гипотенузы.

Задачи на пропорциональность

Решение задач на пропорциональность требует умения работать с пропорциями и находить неизвестные значения. Обычно задачи на пропорциональность можно разделить на два типа:

1. Задачи на пропорцию вида «одно/другое = третье/четвертое»: в таких задачах известно, что одни величины пропорциональны другим. По этим данным требуется найти неизвестное значение или проверить, выполняется ли пропорция.

Пример задачи:

Если 8 мороженых стоят 320 рублей, сколько стоят 12 таких же мороженых?

Решение:

В данной задаче стоимость мороженых пропорциональна их количеству. Для нахождения стоимости 12 мороженых воспользуемся пропорцией:

8 / 320 = 12 / х

где х – неизвестная стоимость 12 мороженых.

Продолжая решение, получим:

8 * х = 320 * 12

х = (320 * 12) / 8

х = 480 рублей.

2. Задачи на пропорцию вида «одно/другое = третье/третье»: в таких задачах известно, что одни величины пропорциональны другим самим себе. По этим данным требуется найти неизвестное значение или проверить, выполняется ли пропорция.

Пример задачи:

Если 6 рабочих сделают 9 деталей за 2 часа, сколько деталей сделают 8 таких же рабочих за 3 часа?

Решение:

В данной задаче количество деталей пропорционально числу рабочих и времени работы. Для нахождения количества деталей воспользуемся пропорцией:

6 / 9 = 8 / х

где х – неизвестное количество деталей.

Продолжая решение, получим:

6 * х = 9 * 8

х = (9 * 8) / 6

х = 12 деталей.

Решая задачи на пропорциональность, важно помнить о правилах составления пропорции и уметь проводить необходимые вычисления. Понимание пропорциональных связей позволяет решить широкий спектр задач из различных областей знаний.

Системы уравнений и неравенств

Система неравенств — это набор нескольких неравенств, которые решаются одновременно. Решением системы неравенств является такой набор значений переменных, при котором все неравенства системы выполняются.

Для решения систем уравнений и неравенств существуют различные методы, такие как метод подстановки, метод сложения/вычитания, метод графического представления и другие.

Одно из основных понятий, связанных с системами уравнений и неравенств, это понятие совместности и несовместности системы. Система уравнений или неравенств называется совместной, если у нее есть хотя бы одно решение. В противном случае, система называется несовместной.

Важно знать основные методы решения систем уравнений и неравенств, а также уметь применять соответствующие формулы и правила, чтобы успешно справиться с задачами, связанными с этой темой.

Ниже приведена таблица с основными формулами, которые необходимо знать для решения систем уравнений и неравенств:

• Формула для нахождения решения системы двух линейных уравнений:
• Формула для нахождения решения системы трех линейных уравнений:
• Формула для нахождения решения системы уравнений вида «квадратное уравнение = линейное уравнение»:
• Формула для нахождения решения системы уравнений вида «квадратное уравнение = число»:
• Формула для нахождения решения системы линейного уравнения и неравенства:
• Формула для нахождения решения системы квадратного уравнения и неравенства:

Это только некоторые из формул, которые могут использоваться при решении систем уравнений и неравенств. Важно запомнить и понять их применение, чтобы успешно решать задачи на ОГЭ по математике.

Планиметрия

Формула/свойствоОписание

Площадь квадрата	Площадь квадрата равна квадрату длины его стороны.
Площадь прямоугольника	Площадь прямоугольника равна произведению длины и ширины.
Площадь треугольника	Площадь треугольника равна половине произведения длины основания и высоты, опущенной на это основание.
Периметр квадрата	Периметр квадрата равен четырем умноженным на длину его стороны.
Периметр прямоугольника	Периметр прямоугольника равен удвоенной сумме его сторон.

Это лишь некоторые из формул и свойств планиметрии, которые могут быть полезны при решении задач на ОГЭ по математике 2022. Рекомендуется запомнить и понять их применение, чтобы успешно справиться с данной темой на экзамене.

Вопрос-ответ:

Какие формулы нужно знать для сдачи ОГЭ по математике в 2022 году?

Для сдачи ОГЭ по математике в 2022 году необходимо знать ряд формул. Некоторые из них: формулы площади и периметра различных фигур (треугольник, прямоугольник, круг), формула площади и объема прямоугольного параллелепипеда, формула площади и объема цилиндра, формула площади и объема шара, формула прямоугольного треугольника (теорема Пифагора), формула среднего арифметического, формула процента и др.

Какие формулы нужно знать для решения задач на площадь и периметр фигур?

Для решения задач на площадь и периметр фигур необходимо знать формулы для их вычисления. Например, для треугольника это формулы площади (S = 0.5 * a * h, где a — основание, h — высота) и периметра (P = a + b + c, где a, b, c — стороны треугольника). Для прямоугольника формулы будут следующие: площадь (S = a * b, где a и b — стороны прямоугольника) и периметр (P = 2 * (a + b)). Для круга формулы: площадь (S = π * r^2, где π — число пи, r — радиус) и периметр (P = 2 * π * r).

Какая формула используется для вычисления объема прямоугольного параллелепипеда?

Для вычисления объема прямоугольного параллелепипеда используется формула V = a * b * h, где a, b и h — длины трех взаимно перпендикулярных ребер параллелепипеда.

Какая формула используется для вычисления объема цилиндра?

Для вычисления объема цилиндра используется формула V = π * r^2 * h, где π — число пи, r — радиус основания цилиндра, h — высота цилиндра.

Что такое формула среднего арифметического?

Формула среднего арифметического позволяет найти среднее значение двух или более чисел. Она выглядит следующим образом: среднее арифметическое = (сумма всех чисел) / (количество чисел). Например, если нужно найти среднее арифметическое чисел 5, 8 и 12, то сумма этих чисел равна 5 + 8 + 12 = 25, а количество чисел равно 3. Подставив значения в формулу, получим среднее арифметическое = 25 / 3 = 8.33.

Видео по теме: