Как успешно сдать ОСАГО по математике в 2021 году: лучшие советы и рекомендации

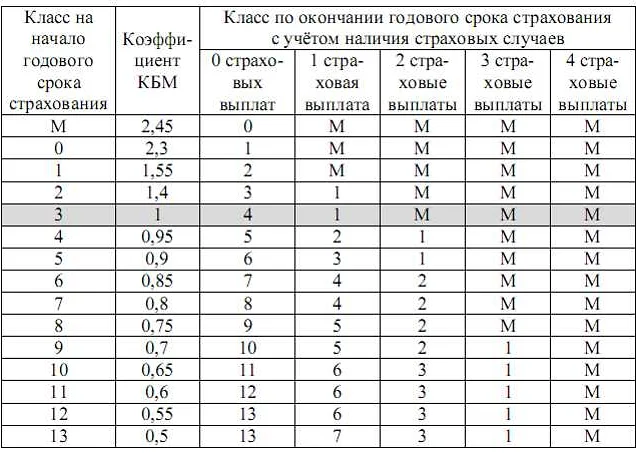
Узнайте, как решать задания ЕГЭ по математике в разделе ОСАГО 2021 года. Мы предлагаем полезные советы и примеры решения задач, которые помогут успешно сдать экзамен и получить высокий балл.

Оценочно-сроковый график основного государственного экзамена по математике в 2021 году уже определен. ОГЭ по математике проходит не только в 9-х классах, но и в 11-х, где основанием для его сдачи является образовательная программа 10-го класса, которая включает в себя курс алгебры и геометрии.

Для успешной сдачи ОГЭ по математике необходимы не только знания, но и умение применять их на практике. Преобладающее количество задач в этом экзамене требуют логического мышления и точной работы со свойствами различных многоугольников, графиками, алгебраическими уравнениями и сетками координат.

Эта статья предназначена для того, чтобы помочь ученикам не только повторить изученный материал, но и научиться эффективным способам решения задач ОГЭ по математике 2021 года.

Понимание условий задачи

Одним из важных аспектов эффективного решения задач по математике на ОГЭ является понимание условий задачи. Ведь, как правило, задания выполняются в ограниченное время, и именно качественное понимание условий задачи позволит быстро и верно решить задание.

Первым шагом к пониманию задачи является внимательное прочтение условия. Необходимо убедиться, что все данные и параметры задачи понятны и не вызывают вопросов. Если возникнут трудности с формулировкой, нужно прочитать задание еще раз или обратиться к учителю за разъяснениями.

Далее, необходимо проанализировать условие задачи и выделить основную информацию. Для этого можно использовать выделение ключевых слов. Если в условии присутствует текстовая информация, ее также следует проанализировать и попытаться связать с математическими понятиями.

Если задача не ясна, не стоит браться за ее решение сразу же. Лучше всего отложить ее на некоторое время и заняться другими заданиями. Позже, когда голова будет отдохнутой, можно вернуться к задаче и попробовать ее решить.

Важно помнить, что в решении задач по математике на ОГЭ, помимо математического знания, большое значение имеет и структура решения. Поэтому аккуратность и внимательность на всех этапах решения задачи будут гарантировать успех.

Точный расчет и использование формул

Для эффективного решения задач Осаго ОГЭ по математике 2021 года необходимо уметь точно рассчитывать данные и использовать формулы. Особенно важно это при решении задач, связанных с расчетом площади, объема, скорости и других величин.

Перед тем, как приступить к решению задачи, необходимо четко определить величины, которые необходимо расчитать. Для этого можно использовать формулы. Например, для расчета площади квадрата можно использовать формулу S=a^2, где а — длина стороны. Это позволит точно рассчитать площадь квадрата в зависимости от данного значения.

При использовании формул необходимо быть внимательным и точным при расчетах. Ошибка в расчетах может привести к неверному ответу и низкому баллу на экзамене. Кроме того, при решении задач необходимо учитывать единицы измерения, которые используются в задаче и правильно их переводить из одной системы в другую.

Важно также учитывать особенности каждой задачи и выбирать подходящие формулы. Например, при расчете скорости можно использовать формулу v=s/t, где s — расстояние, пройденное машиной, а t — время, в течение которого машина прошла это расстояние. Но если задача связана с расчетом средней скорости, то необходимо использовать другую формулу, учитывающую все пройденные участки и время.

Использование точных расчетов и формул является ключевым аспектом при решении задач Осаго ОГЭ по математике 2021 года. Это позволит получить верный ответ и набрать максимальное количество баллов, что является важным для успешной сдачи экзамена.

Работа со сравнениями и отношениями

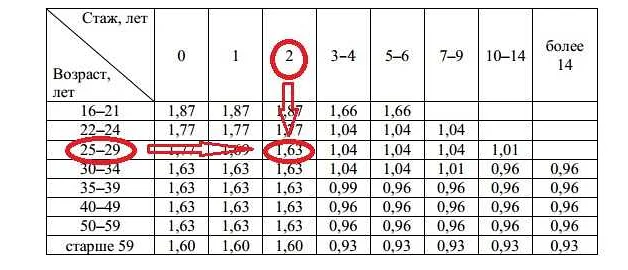
Раздел математики, связанный со сравнениями и отношениями, является важным компонентом ОГЭ по математике. На экзамене часто предлагаются задачи, где необходимо сравнивать числа и находить отношения между ними. Но как быть, если не совсем понятно, как работать со сравнениями и отношениями?

Первое, что нужно запомнить, это правило сравнения чисел. Если a и b — два числа, то:

• a > b — если a больше, чем b
• a < b — если a меньше, чем b
• a = b — если a равно b

Но иногда сравнение чисел бывает не таким простым. Например, если нам нужно сравнить дроби или десятичные дроби. В таких случаях можно использовать различные методы, например:

• перевод дробей в общий знаменатель;
• сравнение чисел в десятичной форме;
• приведение дробей к десятичному виду и сравнение их между собой.

Важно не забывать, что сравнение чисел может быть связано не только с их значением, но и с их величиной. Например, при сравнении скоростей двух транспортных средств важно учитывать не только их абсолютное значение, но и то, какой процент скорости достигается каждым из них.

Если вы научитесь работать со сравнениями и отношениями, вы сможете решать задачи ОГЭ по математике гораздо эффективнее. При решении задач не бойтесь использовать различные методы и действия, которые помогут вам получить правильный ответ.

Применение геометрических преобразований

Геометрические преобразования часто применяются при решении задач на осаго по математике. Они используются для изменения положения фигур на плоскости без изменения их размеров и формы.

Перемещение, поворот и отражение являются основными видами геометрических преобразований. Зная свойства этих преобразований, можно легко решить задачи на осаго, где требуется найти расстояния между точками, углы между прямыми или площадь фигур.

Например, чтобы найти расстояние между двумя точками А и В на плоскости, можно воспользоваться преобразованием перемещения. Перенеся точку А в начало координат, мы получим две новые точки: А'(0,0) и В'(x,y). Теперь легко вычислить расстояние между точками А’ и В’ с помощью формулы \sqrt{x^2+y^2}. Оно будет равно расстоянию между исходными точками А и В.

Также геометрические преобразования помогут найти углы между прямыми или площадь фигур. Чтобы найти угол между двумя прямыми, можно воспользоваться преобразованием поворота. Повернув одну из прямых так, чтобы она стала параллельной другой, мы получим угол между ними, который можно вычислить с помощью соответствующих формул.

Важно знать, как применять геометрические преобразования, чтобы решать задачи на осаго по математике эффективно. Не стоит забывать про комбинации преобразований, которые позволяют добиться нужного результата. Они могут значительно упростить решение задач и помочь получить более высокий балл на экзамене.

Работа с процентами и долями

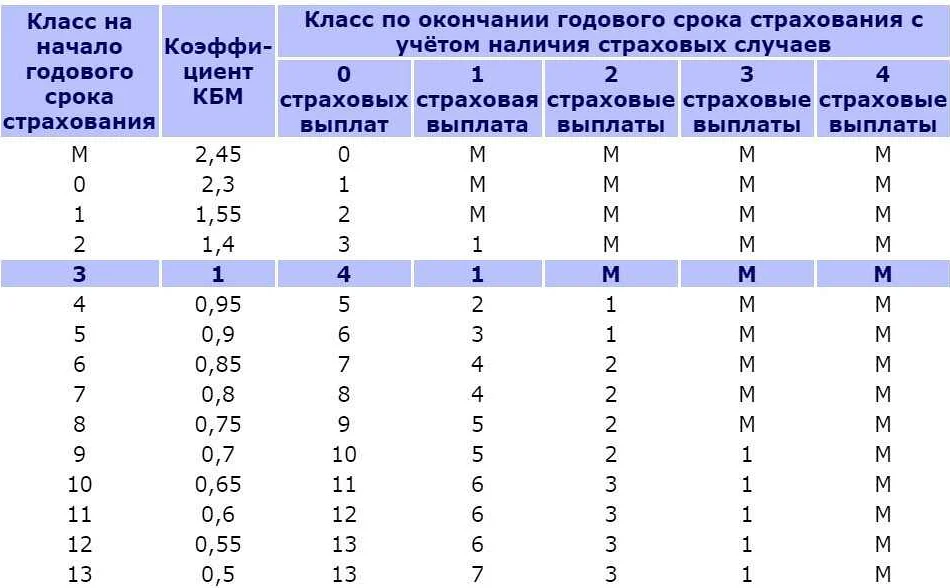
Работа с процентами и долями является важной частью математического анализа. В ОГЭ по математике 2021 она может быть представлена в форме задач на вычисление процентов, нахождение долей и процентных изменений.

В одной из типичных задач на проценты, нам необходимо найти процент от числа. Для этого можно использовать формулу:

Процент от числа = число * (процент / 100)

Например, если нам нужно найти 20% от числа 250, мы можем использовать данную формулу и решить задачу следующим образом:

• 20/100 = 0.2
• 0.2 * 250 = 50

Ответ: 50.

Другой пример может быть задача на вычисление процентного изменения. В данном случае нам необходимо найти, на сколько процентов изменилось одно значение относительно другого:

Процентное изменение = (новое значение — старое значение) / старое значение * 100

Например, если мы знаем, что цена на продукт выросла с 100 до 130 рублей, мы можем найти процентное изменение следующим образом:

• (130 — 100) / 100 * 100 = 30%

Ответ: 30%.

Работа с долями также может быть представлена в виде задач. Доля представляет собой часть значения, которое должно быть разделено на равные части. Решение задач на доли может включать следующий алгоритм:

1. Найти общее количество частей, на которые нужно разделить значение
2. Разделить значение на количество частей, чтобы найти размер одной части
3. Умножить размер одной части на число частей, которые нужны для нахождения нужной доли

Например, если нам нужно найти 1/3 от числа 72, мы можем использовать данный алгоритм следующим образом:

• Общее количество частей: 3
• 72 / 3 = 24 (размер одной части)
• 24 * 1 = 24

Ответ: 24.

Решение задач на движение и расстояние

Задачи на движение и расстояние являются одними из наиболее распространенных в ОГЭ по математике. Для их решения необходимо использовать формулы, а также умение правильно интерпретировать условие задачи.

В первую очередь необходимо определить движущиеся объекты и скорость их перемещения. Обычно это два автомобиля, движущиеся в разных направлениях. Потом необходимо определить начальное расстояние между ними.

Далее можно использовать уравнение расстояния, скорости и времени: S = V*t. Здесь S — расстояние между автомобилями, V — скорость, t — время движения. Необходимо составить два уравнения для каждого автомобиля и решить систему из двух уравнений.

Также можно использовать формулу: S = V1*t1 + V2*t2, где V1 и V2 — скорости автомобилей, t1 и t2 — время, которое они пропорционально движутся. Здесь необходимо учитывать направление движения, так как некоторые задачи могут быть обманчивыми и иметь подвох в виде изменения направления движения.

Некоторые задачи на движение и расстояние могут быть связаны с временем встречи двух объектов. Для их решения необходимо использовать формулу: S1 + S2 = V*(t1+t2), где S1 и S2 — расстояния, которые проходят объекты, V — скорость, t1 и t2 — время движения до встречи.

В целом, чтобы эффективно решать задачи на движение и расстояние, необходимо понимать физические законы и уметь применять соответствующие формулы. Также следует обращать внимание на условия задачи и правильно их интерпретировать.

Применение систем уравнений

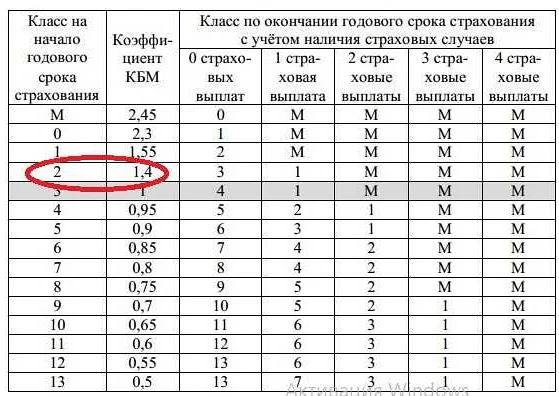
Система уравнений – это математический инструмент, позволяющий решать задачи с несколькими неизвестными величинами, когда для нахождения ответа необходимы одновременно значения нескольких переменных. Применение систем уравнений в задачах ОСАГО может помочь в определении стоимости страховки или размера ущерба после дорожно-транспортного происшествия.

Для решения задач с системами уравнений необходимо выписать уравнения для каждой из переменных, затем соединить их в одну систему и решить методом замены или сложения/вычитания уравнений.

Пример задачи с системой уравнений: «Автомобиль XY при столкновении с автомобилем Z получил повреждения в виде вмятин на обеих дверях. Стоимость ремонта одной вмятины составляет 3000 рублей. Автомобиль Z получил повреждения в виде потери правого зеркала. Стоимость ремонта зеркала составляет 5000 рублей. Стороны договорились о том, что стоимость ремонта будет разделена пропорционально величине ущерба, причиненного каждой из сторон. Определите размер ущерба, причиненного каждой из сторон.»

• Обозначим ущерб, причиненный автомобилю XY, через X.
• Обозначим ущерб, причиненный автомобилю Z, через Z.
• Введем два уравнения для нахождения X и Z:
  X + Z = 8000 (сумма стоимостей ремонта)X : Z = 3 : 5 (в соответствии с договоренностью)
• Решим систему уравнений методом замены:
  X = 2400 (подставляем выражение для X в уравнение 2)Z = 5600 (подставляем выражение для Z в уравнение 1)
• Ответ: ущерб, причиненный автомобилю XY, составляет 2400 рублей, а ущерб, причиненный автомобилю Z, составляет 5600 рублей.

Решение задач на вероятность

Одной из важных тем по математике на ОГЭ является вероятность. Решение задач на эту тему может показаться сложным, но с помощью правильного подхода оно становится довольно простым.

Первым шагом в решении задач на вероятность является определение общего числа исходов. Далее необходимо определить число исходов для каждого возможного события и вычислить вероятность каждого события. Это может быть сделано с помощью различных формул, например, формулы классической вероятности или формулы условной вероятности.

Важно помнить, что вероятность события всегда находится в интервале от 0 до 1, где 0 означает, что событие невозможно, а 1 — что оно обязательно произойдет. Кроме того, вероятности нескольких независимых событий можно перемножать для получения вероятности комбинированного события.

При решении задач на вероятность полезно использовать таблицы и диаграммы, чтобы визуализировать информацию о событиях и вероятностях. Также стоит помнить об основных правилах вероятности, например, о правиле сложения и правиле умножения, и использовать их при решении задач.

И наконец, при решении задач на вероятность стоит быть внимательным и аккуратным при вычислениях, чтобы избежать ошибок и получить правильный ответ.

Упрощение алгебраических выражений

Упрощение алгебраических выражений — это процесс преобразования сложных выражений в более простые, но эквивалентные им по значению. Задача упрощения выражений часто встречается в математике, физике и других науках.

Существует несколько способов упрощения алгебраических выражений. Один из наиболее простых способов — использование правил алгебры, таких как правила дистрибутивности, ассоциативности и коммутативности. Эти правила позволяют переносить переменные между скобками, упрощать сложения и умножения и т.д.

Для сложных выражений может потребоваться более продвинутая техника упрощения, такая как факторизация, использование тригонометрических тождеств или замена переменных. Важно понимать, что упрощение выражений может быть не единственным правильным путем и может зависеть от того, что требуется в конкретной задаче.

Для успешного решения задач ОГЭ по математике 2021 важно уметь упрощать алгебраические выражения, так как многие задачи требуют этого умения. Прежде чем приступать к решению задачи, важно проанализировать ее, определить, какие правила и техники упрощения могут быть применены, и только после этого приступать к решению.

Видео по теме:

Вопрос-ответ:

Какие задачи из ОГЭ по математике можно решить используя алгоритм Евклида?

Алгоритм Евклида можно использовать, например, для решения задач на поиск наибольшего общего делителя двух чисел и для приведения дробей к несократимому виду. Если, например, в задаче нужно найти НОК или НОД двух чисел, то можно воспользоваться этим алгоритмом. Его применение может существенно упростить решение задач.

Какими формулами можно воспользоваться при решении задач на проценты?

При решении задач на проценты помимо формулы простых процентов можно использовать такие формулы, как формула сложных процентов, формула эквивалентности процентных ставок и другие. Очень важно понимать суть этих формул и уметь их правильно применять в разных задачах.

Какие методы могут помочь ускорить решение задач на ОГЭ по математике?

Для ускорения решения задач на ОГЭ по математике можно использовать такие методы, как рисование схем и диаграмм, использование таблиц, использование алгоритмических методов решения, таких как метод перебора или метод ветвей и границ. Также полезной может быть организация работы с задачами, например, планирование времени и составление списка задач, чтобы успеть решить все вопросы.

Какие существуют типы задач на графики на ОГЭ по математике?

На ОГЭ по математике могут встречаться задачи, связанные с графиками функций, задачи на нахождение координат точек на плоскости, задачи на определение углов между прямыми и другие. Для решения таких задач нужно уметь строить и анализировать графики функций, работать с координатными плоскостями и применять геометрические знания.

Какими методами можно решать задачи на комбинаторику на ОГЭ по математике?

Для решения задач на комбинаторику на ОГЭ по математике можно использовать методы перебора, методы комбинаторного анализа, такие как принцип Дирихле, принцип включений-исключений и другие, а также методы использования таблиц и формул. Очень важно уметь правильно применять каждый метод в разных задачах и понимать, какой метод лучше использовать в каждой конкретной ситуации.

Какие формулы нужно знать для решения задач на ОГЭ по математике?

Для решения задач на ОГЭ по математике нужно знать множество формул и правил, таких как формулы на проценты, формулы на геометрию, формулы на тригонометрию, формулы на комбинаторику и другие. Также нужно иметь усвоенные правила решения задач на разные темы, например, на графики, на нахождение площадей и объемов, на решение уравнений и неравенств, на работу с таблицами и графиками. Важно понимать, как и когда применять каждую формулу и правило.

Какие ошибки чаще всего допускают при решении задач на ОГЭ по математике?

Ошибки, которые можно допустить при решении задач на ОГЭ по математике, могут быть разными, но есть несколько наиболее распространенных. В частности, это ошибки в перепутывании единиц измерения, неправильном переносе данных из условия в решение, неудачных заменах и преобразованиях, неправильном выборе метода решения и другие. Чтобы избежать этих ошибок, нужно внимательно читать условия задач и организовывать свою работу так, чтобы не терять важные детали.

Решение задач с применением логики и законов математики

Для эффективного решения задач по ОСАГО на ОГЭ по математике 2021 необходимо знание основных законов математики и умение применять логику.

Для начала, важно уметь правильно формулировать условие задачи и выписывать все данные из текста. Это позволяет получить общее представление о задаче и продвинуться к ее решению.

Далее, умение применять математические законы и формулы позволяет получить точный ответ на задачу. К примеру, для решения задач на расчет пройденного пути, скорости и времени необходимо знание формулы S=V*t.

Также, важно уметь проводить логические выводы на основе данных из задачи и вывести правильный ответ. Часто это применяется в задачах на нахождение количества необходимых материалов или их стоимости в зависимости от данных параметров.

В целом, для успешного решения задач по ОСАГО на ОГЭ по математике 2021 необходимо умение применять логику и математические законы на практике. Первоначально это может показаться сложным, но с определенным опытом и практикой можно достичь высоких результатов.

Проверка результатов и приведение ответов к правильному виду

После решения каждой задачи важно проверять свой результат и убедиться, что он правильный. Для этого можно воспользоваться простыми приёмами, например, применить обратную операцию или подставить полученный ответ в условие задачи.

При проверке результатов необходимо также обратить внимание на то, что ответ должен быть приведён к правильному виду. Например, если требуется ответ в виде дроби, то необходимо её сократить до несократимого вида. Если ответ представляет собой число с запятой, то следует убедиться, что число округлено до необходимого количества знаков после запятой.

Важно помнить, что в ОГЭ за правильный ответ начисляется 2 балла, а за неправильный ответ 0 баллов. Если ответ не является целым числом или дробью и требуется его записать в виде корня или в скобках, то ответ также должен быть записан правильно. При наличии возможности можно использовать программу для проверки правильности написания формул.

Одним из способов привести ответ к правильному виду является использование таблицы перевода единиц измерения. Например, если задача требует ответ в метрах, а решение получено в сантиметрах, то можно воспользоваться таблицей перевода и перевести ответ в метры.

Также для проверки работоспособности решения задачи, можно провести два решения задачи разными способами. Если полученные ответы совпадают, то можно быть уверенным в правильности решения задачи.