Что надо знать по математике в 5 классе

В этой статье вы узнаете основные темы и понятия, которые нужно знать по математике в 5 классе. Узнайте, как решать уравнения, работать с дробями, изучать геометрию и многое другое. Полезная информация для учеников и их родителей!

Математика является одним из основных предметов в школьной программе и имеет большое значение для развития учеников. В 5 классе ученики начинают изучать основные понятия и задачи по математике, которые будут полезны им не только в школе, но и в повседневной жизни.

В первую очередь, ученики изучают основы арифметики. Они учатся складывать, вычитать, умножать и делить числа, а также решать простые задачи, связанные с этими операциями. Важно усвоить правила приоритета операций и научиться применять их на практике.

Другим важным аспектом, который изучается в 5 классе, является работа с дробями. Ученики узнают, как складывать, вычитать, умножать и делить дроби, а также решать задачи, связанные с использованием дробей. Эти навыки позволят им справляться с различными задачами, например, при измерении и сравнении величин.

Кроме того, в 5 классе начинается изучение геометрии. Ученики узнают основные геометрические термины, такие как прямая, отрезок, угол, треугольник и квадрат. Они научатся измерять углы, находить периметр и площадь фигур, а также решать задачи, связанные с геометрией. Эти знания помогут им понимать пространственные отношения и решать задачи, связанные с конструкцией и измерениями.

В итоге, изучение основных понятий и задач по математике в 5 классе является важным этапом в развитии математических навыков и мышления учеников. Эти знания и навыки будут полезны им в дальнейшей учебе и повседневной жизни.

Арифметика и числа

Числа играют важную роль в арифметике. Они делятся на натуральные, целые, рациональные и иррациональные числа.

Натуральные числа — это числа, которые используются для обозначения количества предметов. Они начинаются с единицы и не имеют десятичных дробей.

Целые числа — это натуральные числа вместе со своими отрицательными значениями и нулем.

Рациональные числа — это числа, которые можно представить в виде обыкновенной или десятичной дроби. Они могут быть представлены в виде отношения двух целых чисел.

Иррациональные числа — это числа, которые нельзя представить в виде дроби. Они имеют бесконечную десятичную дробь, которая не повторяется.

В арифметике используются различные методы и техники для решения задач. Одним из основных методов является ручное вычисление.

Важно понимать основные понятия и задачи по арифметике и числам, чтобы успешно изучать более сложные темы в математике.

Геометрия и фигуры

В геометрии важно понимать основные понятия, такие как:

• Точка — это наименьший элемент геометрической фигуры, не имеющий размеров.
• Линия — это набор точек, которые продолжаются в обе стороны бесконечно.
• Отрезок — это часть линии, ограниченная двумя точками.
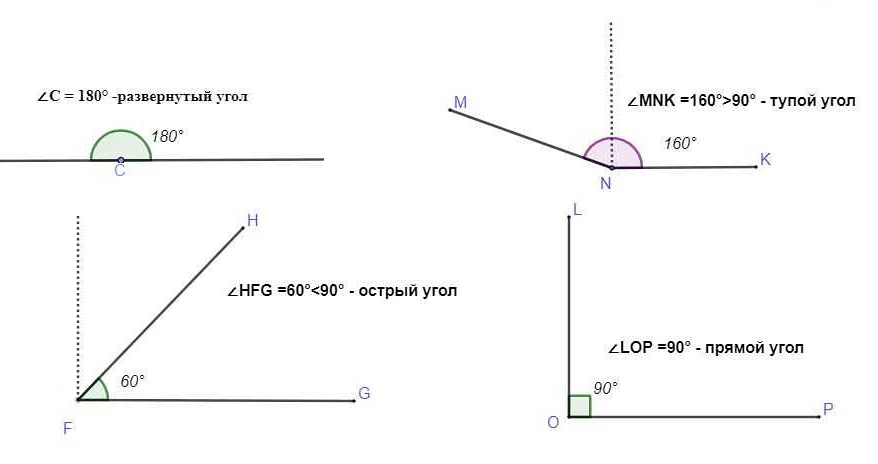
• Угол — это область между двумя линиями или отрезками, соединяющими общую точку.
• Многоугольник — это фигура с прямыми сторонами, состоящая из трех или более отрезков.
• Тело — это трехмерный геометрический объект, имеющий длину, ширину и высоту.

В геометрии также рассматриваются различные виды фигур, такие как:

• Круг — это фигура, все точки которой находятся на одинаковом расстоянии от центра.
• Треугольник — это многоугольник с тремя сторонами.
• Прямоугольник — это многоугольник с четырьмя прямыми углами.
• Квадрат — это прямоугольник, у которого все стороны равны.
• Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны.
• Трапеция — это четырехугольник, у которого две стороны параллельны.

Изучая геометрию и фигуры, мы можем решать задачи, связанные с измерением длины, площади и объема. Также геометрия помогает нам развивать воображение и пространственное мышление, что полезно не только в математике, но и в повседневной жизни.

Рациональные числа и десятичные дроби

Десятичные дроби — это способ представления рациональных чисел, где числитель разделен на знаменатель с помощью десятичной точки. Например, число 0.5 представляет собой десятичную дробь, соответствующую рациональному числу 1/2.

Для работы с рациональными числами и десятичными дробями важно понимать их основные свойства и операции. С помощью рациональных чисел можно выполнять арифметические действия, такие как сложение, вычитание, умножение и деление. Для работы с десятичными дробями также необходимо знать, как округлять числа и выполнять операции с округленными значениями.

Важно помнить, что рациональные числа и десятичные дроби широко используются в реальной жизни для измерения и представления различных величин. Например, десятичные дроби используются для измерения длины, веса, времени и денежных сумм.

Освоение понятий рациональных чисел и десятичных дробей является важной задачей в 5 классе. Это позволит ученикам успешно выполнять математические операции, решать задачи и развивать логическое мышление.

Алгебра и уравнения

Основным понятием алгебры является переменная. Переменная — это символ, который может принимать различные значения. Ученики учатся работать с переменными и выполнять арифметические операции над ними.

Важным элементом алгебры являются уравнения. Уравнение — это математическое выражение, в котором сравниваются два выражения с помощью знака равенства. Задача уравнения — найти значение переменной, при котором оба выражения равны.

В 5 классе ученики изучают простые линейные уравнения с одной переменной. Они учатся составлять и решать такие уравнения. Для решения уравнений используются различные методы, такие как применение простых арифметических действий или преобразование уравнения.

Уравнения в алгебре имеют широкое применение в решении различных задач. Они помогают находить неизвестные значения и находить зависимости между различными величинами. Освоение алгебры и умение работать с уравнениями помогает ученикам развивать логическое мышление и аналитические навыки.

Понимание основных понятий и задач алгебры в 5 классе является важным шагом в изучении математики и подготовке к более сложным темам в будущем.

Пропорции и проценты

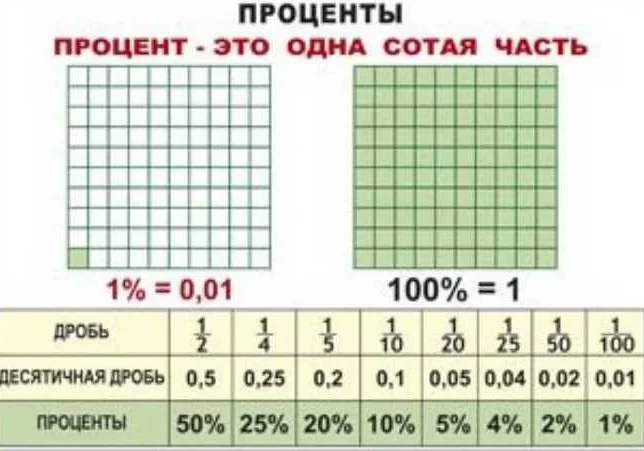
Пропорции можно решать различными способами. Один из них — использование процентов. Процент — это доля или часть от целого, выраженная в сотых долях. Он позволяет выразить одну величину относительно другой и сравнить их.

Расчет процентов осуществляется с помощью формулы: процент = (часть / целое) * 100%. Например, если из 100 школьников 75 получили высокую оценку, то процент школьников с высокой оценкой будет равен (75 / 100) * 100% = 75%.

Проценты также используются для нахождения неизвестных значений в пропорциях. Например, если известно, что 20% людей в городе занимаются спортом, а общее количество жителей составляет 5000 человек, то можно найти, сколько людей занимается спортом. Для этого нужно вычислить 20% от 5000, т.е. (20 / 100) * 5000 = 1000 человек.

Пропорции и проценты — важные понятия в математике, которые помогают анализировать и сравнивать различные величины в реальной жизни. Они позволяют нам делать выводы, прогнозировать и принимать решения на основе количественных данных.

Статистика и вероятность

В статистике мы учимся собирать данные и представлять их с помощью различных графиков, таких как диаграммы и столбчатые графики. Мы также узнаем, как анализировать данные и находить основные характеристики выборки, такие как среднее значение, медиана и мода.

Вероятность — это вероятность того, что определенное событие произойдет или не произойдет. Мы изучаем основные понятия вероятности, такие как эксперимент, исходы, события, и вероятность события. Мы также узнаем, как вычислять вероятность событий, используя формулы и диаграммы Венна.

Основные задачи статистики и вероятности включают в себя сбор и анализ данных, представление данных с помощью графиков, определение и интерпретацию основных характеристик выборки, а также вычисление вероятности событий. Знание этих понятий и навыки помогут нам в понимании статистики и вероятности в повседневной жизни, а также в решении различных математических задач.

Измерение и единицы измерения

Единицы измерения — это стандартные величины, используемые для измерения различных физических величин. Они позволяют сравнивать разные объекты и определять их отношение друг к другу.

Существует множество единиц измерения. Вот некоторые из них:

• Длина:
  • Метр (м)
  • Километр (км)
  • Сантиметр (см)
  • Миллиметр (мм)
• Масса:
  • Килограмм (кг)
  • Грамм (г)
  • Тонна (т)
• Время:
  • Секунда (с)
  • Минута (мин)
  • Час (ч)
  • День (дн)
• Объем:
  • Литр (л)
  • Миллилитр (мл)

Изучение измерения и единиц измерения поможет вам понять и использовать различные величины в математике и реальной жизни. Оно также поможет вам выполнять задачи связанные с измерениями и конвертировать значения между разными единицами измерения.

Вопрос-ответ:

Что такое десятичные дроби?

Десятичные дроби — это числа, которые записываются после запятой. Они состоят из цифр от 0 до 9, и каждая цифра в десятичной дроби имеет свое место, которое определяет ее значение.

Какие задачи можно решать с использованием пропорций?

Пропорции используются для решения задач, связанных с сравнением двух или более величин. Например, с помощью пропорции можно решить задачи на нахождение неизвестных значений, если известны соотношения между величинами.

Что такое геометрические фигуры?

Геометрические фигуры — это объекты, обладающие определенными геометрическими свойствами. К ним относятся такие фигуры, как круг, квадрат, треугольник, прямоугольник и многие другие. Каждая геометрическая фигура имеет свою форму, размеры и свойства.

Какие понятия и задачи изучаются в математике в 5 классе?

В математике в 5 классе изучаются такие понятия, как десятичные дроби, пропорции, геометрические фигуры, длины, площади и объемы, проценты, таблицы и диаграммы. Задачи включают решение уравнений, составление расписаний, работу с графиками и другие практические задачи.

Графики и диаграммы

Столбчатые диаграммы представляют данные с помощью вертикальных столбцов разной высоты. Высота каждого столбца соответствует значению, которое необходимо представить. Такие диаграммы удобно использовать для сравнения количественных данных.

Круговые диаграммы представляют данные в виде круга, разделенного на секторы. Площадь каждого сектора пропорциональна значению, которое он представляет. Круговые диаграммы помогают увидеть соотношение частей к целому и сравнить их между собой.

Линейные графики позволяют отобразить изменение значения величины на протяжении времени или по другой шкале. Они состоят из точек, соединенных линиями. Линейные графики позволяют анализировать тенденции и прогнозировать будущие значения.

Точечные диаграммы используются для отображения зависимости двух переменных. Они состоят из точек, расположенных на координатной плоскости. Точечные диаграммы помогают выявить взаимосвязь между переменными и определить характер этой связи (прямая, обратная, отсутствие связи).

Изучение графиков и диаграмм помогает развивать умение анализировать и интерпретировать информацию, а также принимать обоснованные решения на основе полученных результатов. Они широко используются в реальной жизни, в науке, экономике, маркетинге и других сферах деятельности.

Видео по теме: