Основные законы математики которые должен знать каждый

В статье рассказывается о важных математических законах, которые должен знать каждый. На примерах и объяснениях их применения вы узнаете о законе ассоциативности, коммутативности, дистрибутивности и других основных правилах, необходимых для понимания и применения математики в повседневной жизни.

Математика — это наука о числах, структурах, пространстве и изменениях. Она играет важную роль в нашей повседневной жизни, помогая нам развивать логическое мышление и решать различные задачи. Независимо от того, занимаетесь ли вы наукой или искусством, понимание основных законов математики является необходимым.

Один из основных законов математики — закон ассоциативности. Он гласит, что порядок, в котором мы выполняем операции сложения или умножения, не влияет на результат. Например, для любых чисел a, b и c, (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c). Закон ассоциативности помогает нам упростить сложные выражения и делает математические операции более удобными.

Еще один важный закон — закон коммутативности. Он утверждает, что порядок чисел, с которыми мы выполняем операции сложения или умножения, не влияет на результат. Например, для любых чисел a и b, a + b = b + a и a * b = b * a. Закон коммутативности помогает нам менять порядок слагаемых или множителей, не изменяя значения выражений.

Еще один фундаментальный закон — закон дистрибутивности, который объединяет операции сложения и умножения. Он гласит, что a * (b + c) = (a * b) + (a * c). Например, если у нас есть выражение 2 * (3 + 4), мы можем распределить умножение на оба слагаемых и получить результат 2 * 3 + 2 * 4. Закон дистрибутивности очень полезен при упрощении выражений и решении уравнений.

Знание основных законов математики поможет вам развить аналитическое мышление, решать сложные задачи и логически аргументировать свои решения. Расширение своих знаний в этой области может быть полезно не только в школьной математике, но и в повседневной жизни и различных сферах деятельности.

Закон ассоциативности операций

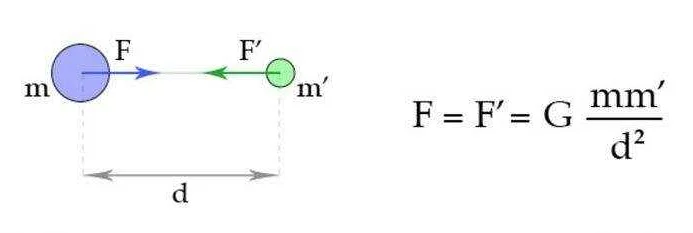
Другими словами, если имеется операция «*»:

(a * b) * c = a * (b * c)

Закон ассоциативности действует в различных областях математики, таких как алгебра, арифметика и теория множеств. Он позволяет менять порядок выполнения операций и группировать элементы по своему усмотрению без изменения результатов.

Например, в алгебре закон ассоциативности позволяет переставлять скобки при выполнении операций с числами или переменными:

(2 + 3) + 4 = 2 + (3 + 4) = 9

Также этот закон используется при решении уравнений и систем уравнений, где порядок выполнения действий может быть произвольным.

Знание закона ассоциативности операций является важным для понимания и использования математических концепций и позволяет сокращать количество вычислений и упрощать решение задач.

Видео по теме:

Закон коммутативности операций

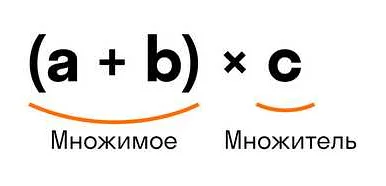
Например, в арифметике закон коммутативности применяется к операциям сложения и умножения. Для сложения это означает, что порядок слагаемых не важен. Например, 2 + 3 будет равно 3 + 2.

Аналогично, для умножения это означает, что порядок множителей не играет роли. Например, 4 * 5 будет равно 5 * 4.

Закон коммутативности также применяется в других областях математики, например, в алгебре. В алгебре этот закон позволяет менять порядок слагаемых или множителей в выражении без изменения результата.

Закон дистрибутивности операций

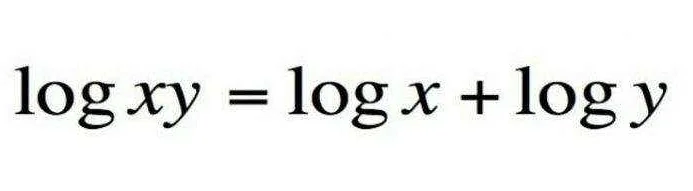
Этот закон формулируется следующим образом:

Для любых трех чисел a, b и c выполняется следующее равенство:

a * (b + c) = a * b + a * c

или

(b + c) * a = b * a + c * a

Это означает, что умножение числа a на сумму двух чисел b и c равно сумме умножения числа a на число b и числа a на число c.

Закон дистрибутивности операций широко применяется в алгебре и арифметике для упрощения выражений и выполнения операций с числами.

Пример применения закона дистрибутивности:

Пусть у нас есть выражение 2 * (3 + 4). Согласно закону дистрибутивности, это выражение можно переписать следующим образом:

2 * (3 + 4) = 2 * 3 + 2 * 4 = 6 + 8 = 14

Таким образом, мы получили, что выражение 2 * (3 + 4) равно 14.

Знание закона дистрибутивности операций позволяет сокращать и упрощать выражения, а также выполнять операции с числами более эффективно.

Закон единицы

Символ единицы обозначается как «1». Он является нейтральным элементом для умножения и сложения чисел. Это означает, что умножение или сложение любого числа на единицу не меняет его значения.

Например, 5 умноженное на единицу равно 5: 5 * 1 = 5. Также, 7 плюс единица равно 8: 7 + 1 = 8.

Закон единицы широко используется в математике и других науках. Он помогает в решении уравнений, проведении вычислений и решении различных задач.

Закон единицы также имеет свои аналоги в других областях, например, в физике. Например, в физических уравнениях, единицы измерения играют роль аналогичную единице в математике.

Закон нуля

0 + a = a

Здесь 0 — это нулевой элемент, а a — любое число. Интуитивно, закон нуля может показаться очевидным, ведь ноль ничего не меняет. Однако, это важное математическое правило, которое используется во многих областях математики.

Закон нуля можно применять в арифметических операциях, таких как сложение и вычитание. Например, если нужно сложить число 7 и ноль, то результатом будет число 7:

7 + 0 = 7

Также, закон нуля может быть полезен при решении уравнений. Если в уравнении присутствует сумма с нулевым элементом, то эту сумму можно упростить, оставив только другое слагаемое. Например, рассмотрим уравнение:

3x + 0 = 9

Согласно закону нуля, сумма 0 и любого числа равна этому числу, поэтому можно упростить уравнение следующим образом:

3x = 9

Закон нуля является основой для понимания большего числа математических концепций и применяется в различных областях математики, таких как алгебра, арифметика, геометрия и другие.

Закон отрицания

Другими словами, если у нас есть утверждение «A», то отрицание этого утверждения будет «не A». Например, если утверждение «A» — «Сегодня идет дождь», то отрицание этого утверждения будет «не A» — «Сегодня не идет дождь».

Закон отрицания широко используется в математике, логике и других областях знания. Он позволяет нам строить правильные рассуждения и доказательства, основываясь на логических операциях отрицания.

Закон двойного отрицания

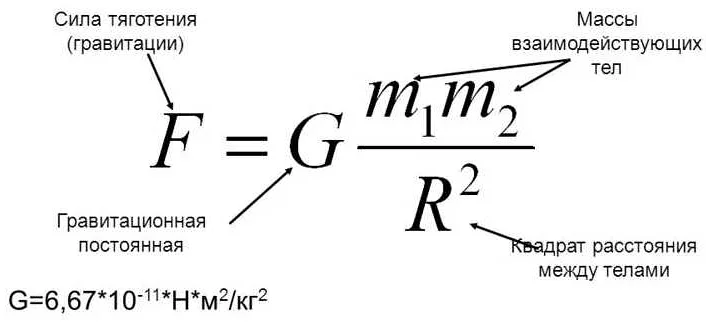
Например, если утверждение A звучит: «Сегодня солнечный день», то его отрицание будет звучать как: «Сегодня не солнечный день». Двойное отрицание этого утверждения будет звучать так: «Сегодня солнечный день». То есть, двойное отрицание подтверждает первоначальное утверждение.

Закон двойного отрицания широко применяется в логике и математике. Он позволяет упрощать логические выражения, избегая двойного отрицания и возвращаясь к исходному значению. Знание этого закона помогает строить логические цепочки и доказательства, а также делает работу с математическими выражениями более удобной и эффективной.

Закон де Моргана

Первая формулировка закона де Моргана гласит, что отрицание конъюнкции двух высказываний равно дизъюнкции отрицаний этих высказываний.

Формула: ¬(A ∧ B) = ¬A ∨ ¬B

То есть, если высказывания A и B имеют истинное значение, то отрицание конъюнкции A и B будет иметь ложное значение. Обратно, если отрицание высказывания A или отрицание высказывания B имеют истинное значение, то конъюнкция A и B будет иметь ложное значение.

Вторая формулировка закона де Моргана гласит, что отрицание дизъюнкции двух высказываний равно конъюнкции отрицаний этих высказываний.

Формула: ¬(A ∨ B) = ¬A ∧ ¬B

Эта формула устанавливает, что если высказывание A или высказывание B имеют истинное значение, то отрицание дизъюнкции A и B будет иметь ложное значение. Обратно, если отрицание высказывания A и отрицание высказывания B имеют истинное значение, то дизъюнкция A и B будет иметь ложное значение.

Закон де Моргана является важным инструментом для преобразования выражений и упрощения логических операций. Он позволяет заменять сложные выражения эквивалентными, но более простыми.

Например:

¬(A ∨ B) = ¬A ∧ ¬B

¬(A ∧ B) = ¬A ∨ ¬B

Знание и применение закона де Моргана позволяет эффективно работать с логическими операциями и улучшить понимание принципов математики.

Вопрос-ответ:

Какие основные законы математики существуют?

Основными законами математики являются законы коммутативности, ассоциативности и дистрибутивности. Эти законы позволяют изменять порядок операций и группировать числа при выполнении математических операций.

Что такое закон коммутативности?

Закон коммутативности гласит, что порядок слагаемых или множителей не влияет на результат операции. Например, при сложении чисел 2 и 3 результат будет одинаковым, независимо от того, сначала мы прибавим 2 и затем 3, или наоборот.

Как работает закон ассоциативности?

Закон ассоциативности утверждает, что результат операции не зависит от того, какой порядок группировки используется при выполнении операций. Например, при сложении трех чисел 2, 3 и 4 результат будет одинаковым, независимо от того, сначала мы сложим 2 и 3, а затем результат сложим с 4, или наоборот.

Для чего нужен закон дистрибутивности?

Закон дистрибутивности позволяет распространять операции между числами при выполнении сложных выражений. Например, при умножении числа на сумму двух чисел, можно сначала умножить число на каждое слагаемое, а затем сложить результаты.

Какие еще законы математики существуют?

Помимо законов коммутативности, ассоциативности и дистрибутивности, существуют также законы и свойства отношений порядка, законы де Моргана, законы и свойства логарифмов, а также законы и свойства экспоненты.

Какие основные законы математики необходимо знать каждому?

Основные законы математики, которые необходимо знать каждому, включают законы арифметики (сложение, вычитание, умножение, деление), закон ассоциативности, закон коммутативности и закон дистрибутивности. Также важно знать закон эквивалентности, закон противоположных чисел, закон отрицания, закон дополнения и закон исключенного третьего.

Что такое закон ассоциативности в математике?

Закон ассоциативности является одним из основных законов математики. Он гласит, что порядок выполнения операций в арифметическом выражении не влияет на его результат, если операции выполняются над одним и тем же числом. Например, для любых трех чисел a, b и c, (a + b) + c = a + (b + c). Закон ассоциативности применяется в алгебре, геометрии и других областях математики.