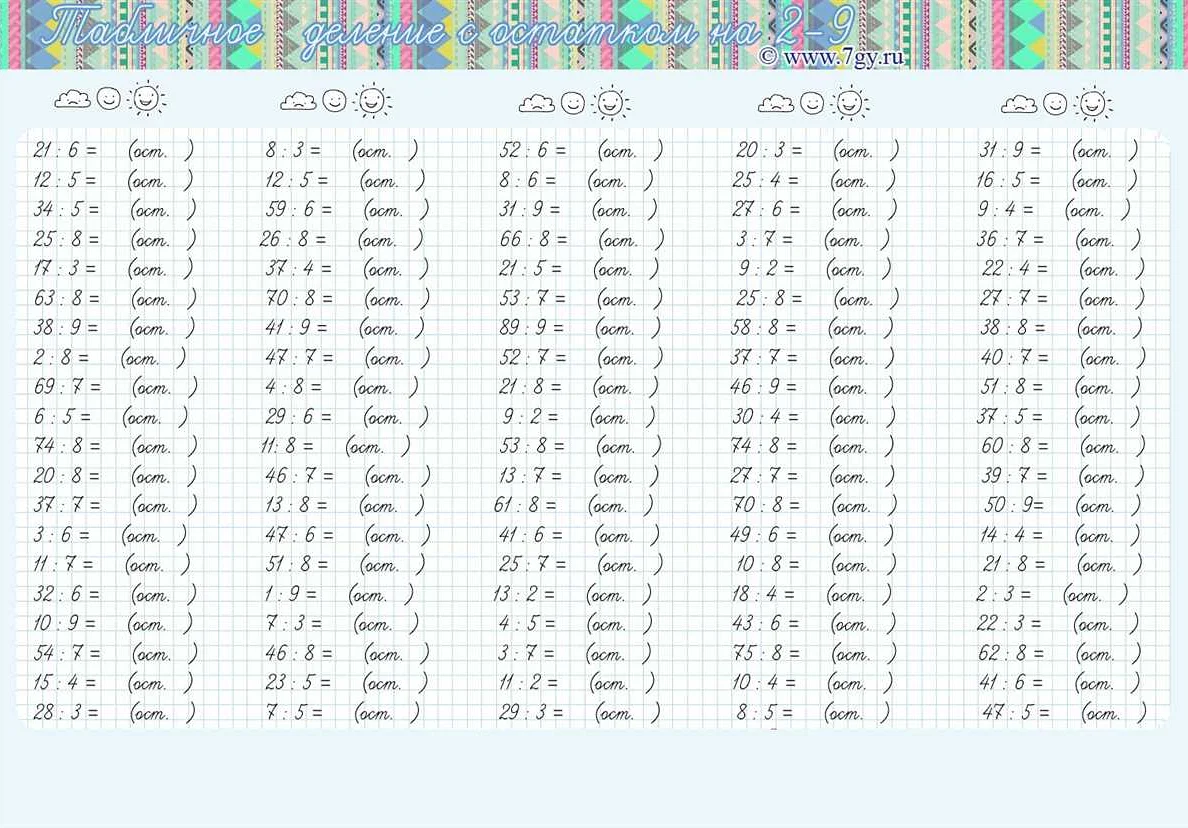
Остаток в математике 3 класс: что это такое и примеры расчетов
Содержимое
- 1 Остаток в математике 3 класс: что это такое и примеры расчетов
- 1.1 Остаток в математике 3 класс
- 1.2 Видео по теме:
- 1.3 Что такое остаток и зачем он нужен
- 1.4 Как находить остаток деления чисел и примеры
- 1.5 Вопрос-ответ:
- 1.5.0.1 Что такое остаток в математике?
- 1.5.0.2 Зачем нужен остаток?
- 1.5.0.3 Как вычислить остаток?
- 1.5.0.4 Можно ли остаток получить при делении на десять?
- 1.5.0.5 Как применять остаток на практике в школьной программе?
- 1.5.0.6 Можно ли получить остаток от деления дробного числа?
- 1.5.0.7 Как отличить остаток от частного?
- 1.6 Применение остатка в задачах на сложение и вычитание
- 1.7 Остаток и умножение чисел, задачи по упрощению выражений
- 1.8 Остаток как инструмент проверки корректности вычислений
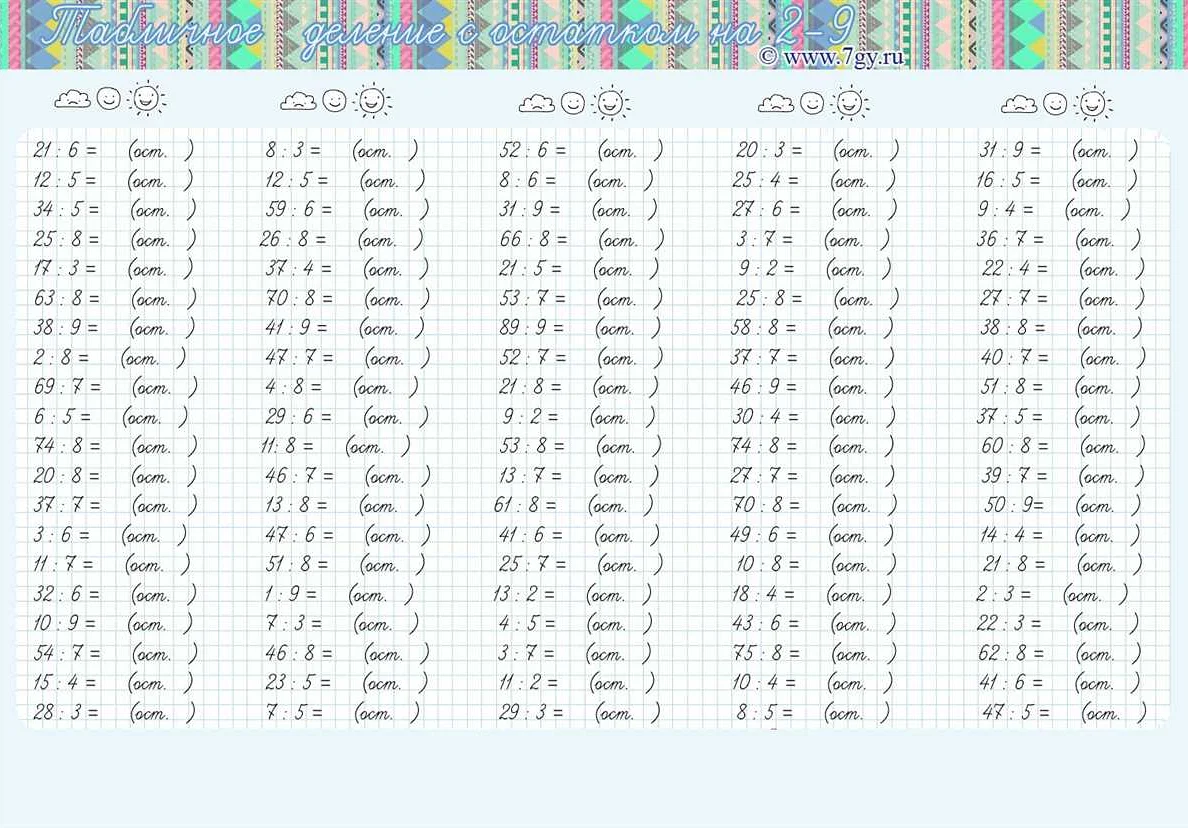
- 1.9 Таблица остатков для чисел от 1 до 10
- 1.10 Остаток и числа четные/нечетные, задачи на сумму и разность четных и нечетных чисел
- 1.11 Остаток как инструмент при решении задач на распределение предметов и вещей
- 1.12 Примеры задач на остаток в математике для 3 класса
- 1.13 Остаток и работа со временем: задачи на время и часы
- 1.14 Выводы о применении остатка в математике и его пользе для учеников
Остаток в математике для 3 класса – это число, которое остается после выполнения деления нацело. В статье приведены примеры задач с решением, помогающие лучше освоить эту тему в школьной программе.
Остаток — это математическое понятие, которое используется для определения остатка после деления одного числа на другое. В третьем классе ученики знакомятся с основами деления и могут начать изучать понятие остатка. Эта тема позволяет детям лучше понимать математические операции и решать различные задачи.
Применение остатка в математике может быть различным. Она может помочь ученикам определить четность или нечетность числа, найти остатки после деления и решить задачу, связанную с долей. Кроме того, знание остатка может помочь в решении задач на подбор чисел и ряда других математических задач.
В статье мы рассмотрим основное понятие остатка в математике 3 класса, а также покажем, как применять его на примерах. Мы проведем небольшой обзор идеи остатка и раскроем несколько тематических примеров, в которых четность, нечетность и остаток важны для решения задач. В конце статьи вы получите инструменты и информацию, которые помогут вам решать задачи с остатком в математике 3 класса.
Остаток в математике 3 класс
Остаток – это число, которое остается после того, как одно число делится на другое. В математике остаток обозначается символом %.
Например, если мы разделим число 17 на 5, мы получим остаток 2, потому что 17 = 3 * 5 + 2. Здесь 3 — это результат деления 17 на 5 без остатка, а 2 — это остаток.
В математике 3 класса остаток используется для решения задач на делимость и проверки правильности вычислений.
Например, задача может быть сформулирована так: Разделите 87 на 6 и найдите остаток. Решение: 87 = 14 * 6 + 3, поэтому остаток равен 3.
Если мы сделали вычисления с помощью остатка, то мы можем проверить свой ответ, подставив полученные значения обратно в задачу и убедившись, что равенство выполняется.
Знание того, что такое остаток и как его применять, поможет ученикам справляться с задачами по математике 3 класса и начать понимать более сложные понятия делимости.
Видео по теме:
Что такое остаток и зачем он нужен
Остаток — это число, которое остается после того, как мы разделили одно число на другое. Например, если мы разделим 10 на 3, то получим 3, в котором остается остаток 1.
Остаток имеет много применений. Он позволяет нам решать задачи на деление с остатком, например, определять остаток от деления числа на 2 (если остаток 0, то число четное, если 1 — нечетное).
Остаток также используется в модульной арифметике, которая широко применяется в криптографии, информатике и других областях. В модульной арифметике остаток вычисляется по определенному модулю.
Например, остаток числа 27 по модулю 5 равен 2, потому что 27 = 5 x 5 + 2. Это может быть полезным для кодирования информации и защиты данных.
В заключение, остаток — это важная математическая концепция, которая имеет много применений в различных областях знаний.
Как находить остаток деления чисел и примеры
Остаток – это число, которое остается после деления одного числа на другое. Остаток деления можно найти с помощью математической операции модуль (%). При делении числа A на число B с остатком получим остаток R. Это означает, что мы можем написать выражение для остатка: A % B = R.
Вот несколько примеров:
- 12 % 5 = 2, потому что 12 делится на 5 два раза с остатком 2
- 20 % 4 = 0, потому что 20 без остатка делится на 4
- 7 % 3 = 1, потому что 7 делится на 3 два раза с остатком 1
Найти остаток может быть полезно, когда мы работаем с массивами или когда нужно определить четность или нечетность числа. Также остаток может быть использован для нахождения цикличности в последовательности чисел.
Вопрос-ответ:
Что такое остаток в математике?
Остаток — это число, которое остается при делении одного числа на другое. Например, если мы делим 10 на 3, то остаток будет равен 1, так как 10 = 3 * 3 + 1.
Зачем нужен остаток?
Остаток используется в различных математических задачах. Например, если нужно поделить конфеты на группы равными порциями, то остаток покажет, сколько конфет останется после деления. Остаток также используется в математических алгоритмах.
Как вычислить остаток?
Остаток можно вычислить с помощью оператора % (модуль) в большинстве языков программирования, а также с помощью деления в столбик. Например, чтобы посчитать остаток от деления 10 на 3, нужно написать: 10 % 3 = 1.
Можно ли остаток получить при делении на десять?
Да, при делении на десять остаток будет равен последней цифре числа. Например, остаток от деления 456 на 10 будет равен 6.
Как применять остаток на практике в школьной программе?
Остаток используется, например, для определения четности или нечетности числа, для выделения цифр в числе, для определения кратности и для решения задач на деление.
Можно ли получить остаток от деления дробного числа?
Да, можно. Для этого нужно записать дробь в виде десятичной дроби и найти остаток от деления десятичной дроби на число. Например, остаток от деления 1,5 на 0,5 будет равен 0.
Как отличить остаток от частного?
Частное — это результат деления одного числа на другое, а остаток — остаток от деления. Например, если мы делим 10 на 3, то частное будет равно 3, а остаток будет равен 1.
Применение остатка в задачах на сложение и вычитание
Остаток может быть очень полезным инструментом в решении задач на сложение и вычитание. Например, рассмотрим задачу:
Ваня купил 15 конфет и 9 печенья. Сколько всего единиц товара купил Ваня?
Для решения этой задачи нужно сложить количество конфет и печенья:
15 + 9 = 24
Получаем, что Ваня купил 24 единицы товара. Однако, интересно знать, сколько товара осталось у Вани после покупки. Для этого можно применить остаток.
Остаток можно получить, вычитая из всего количества товара (24) количество купленного товара (15 конфет и 9 печенья):
24 — 15 — 9 = 0
Получается, что у Вани после покупки не осталось никакого товара. Эта информация также может быть полезна в решении некоторых задач.
Другой пример задачи, которую можно решить с помощью остатка:
У Ани было 37 рублей. Она потратила 15 рублей на мороженое и 8 рублей на сладости. Сколько раблей осталось у Ани?
Для решения этой задачи нужно вычесть из изначальной суммы (37) количество потраченных денег:
37 — 15 — 8 = 14
Ани осталось 14 рублей.
Таким образом, остаток может быть полезным инструментом в решении задач на сложение и вычитание, когда нужно знать, сколько товара или денег осталось после покупки или потраты.
Остаток и умножение чисел, задачи по упрощению выражений
Остаток в математике — это число, которое остается после того, как одно число делится на другое. Например, при делении 10 на 3, остаток будет равен 1. Остаток может быть положительным или отрицательным, но он всегда меньше делителя.
Умножение чисел — это операция, при которой два числа перемножаются, чтобы получить новое число. Например, умножение чисел 3 и 4 даст результат 12.
Для упрощения выражений с умножением чисел и остатком часто используется таблица умножения и таблица остатков. Эти таблицы могут помочь быстрее и проще решать задачи, связанные с математическими операциями.
Например, выражение 3·5 + 2 mod 6 может быть упрощено следующим образом: 3·5 равняется 15, а 15 + 2 дают в итоге 17. Затем, остаток от деления 17 на 6 будет равен 5.
Другой пример задачи на упрощение выражения: умножить число 4 на остаток от деления 15 на 7. В таблице остатков для делителя 7 найдем значение 15, которое будет равно 1. После этого, умножаем 4 на 1 и получаем ответ 4.
Таким образом, остаток и умножение чисел могут быть использованы для упрощения выражений в математике. Знание таблиц умножения и остатков может значительно облегчить решение задач и избежать ошибок при решении математических выражений.
Остаток как инструмент проверки корректности вычислений

Остаток – это число, оставшееся после того, как одно число разделено на другое без остатка. Например, если мы разделим 12 на 5, мы получим остаток 2.
Остаток может быть полезным инструментом для проверки корректности вычислений. Если мы знаем, что должно получиться определенное значение, мы можем использовать остаток для проверки, правильно ли выполняются вычисления.
Например, если мы хотим проверить, правильно ли мы выполняем вычисление 14 + 27 = 41, мы можем использовать остаток. Мы знаем, что 41 должно делиться на 7 без остатка, потому что 7 является делителем как 14, так и 27. Мы можем найти остаток от деления 41 на 7 и убедиться, что он равен нулю.
Еще один пример использования остатка для проверки корректности – это при вычислении площади прямоугольника. Если мы знаем, что площадь должна быть равна произведению длины и ширины, мы можем использовать остаток для проверки, правильно ли мы выполняем вычисления. Например, если длина равна 6, а ширина равна 4, мы должны получить площадь, равную 24. Мы можем использовать остаток, чтобы убедиться, что 24 делится на 6 без остатка, так как длина является делителем 24.
Таблица остатков для чисел от 1 до 10
Остаток числа — это число, которое остается при делении одного числа на другое.
Для примера, при делении числа 11 на 3, получится остаток 2, так как 11 = 3*3 + 2.
Таблица остатков для чисел от 1 до 10:
ДелительОстаток при делении 1Остаток при делении 2Остаток при делении 3Остаток при делении 4Остаток при делении 5Остаток при делении 6Остаток при делении 7Остаток при делении 8Остаток при делении 9Остаток при делении 10
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 |
| 4 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 |
| 5 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 0 |
| 6 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 |
| 7 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 |
| 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 0 | 1 |
| 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
Использование таблицы остатков может быть полезным при решении задач на деление и при поиске чисел, кратных определенному числу.
Остаток и числа четные/нечетные, задачи на сумму и разность четных и нечетных чисел

Прежде чем перейти к задачам на сумму и разность четных и нечетных чисел, нужно разобраться в понятии «четное» и «нечетное».
Четные числа — это числа, которые делятся на 2 без остатка. Например, 2, 4, 6, 8 и так далее.
Нечетные числа — это числа, которые не делятся на 2 без остатка. Например, 1, 3, 5, 7 и так далее.
Теперь можно приступить к задаче на сумму и разность четных и нечетных чисел. Например, требуется найти разность между суммой четных чисел от 1 до 10 и суммой нечетных чисел от 1 до 10.
Для решения этой задачи нужно вычислить сумму четных чисел от 1 до 10 (2 + 4 + 6 + 8 + 10 = 30) и сумму нечетных чисел от 1 до 10 (1 + 3 + 5 + 7 + 9 = 25).
Разность между этими суммами равна 30 — 25 = 5. Значит, разность между суммой четных чисел от 1 до 10 и суммой нечетных чисел от 1 до 10 равна 5.
Также можно задать обратную задачу — найти сумму четных чисел от 1 до 10 и сумму нечетных чисел от 1 до 10 и найти их сумму.
Сумма четных чисел от 1 до 10 равна 2 + 4 + 6 + 8 + 10 = 30, а сумма нечетных чисел от 1 до 10 равна 1 + 3 + 5 + 7 + 9 = 25. Сумма этих двух чисел равна 30 + 25 = 55. Значит, сумма четных и нечетных чисел от 1 до 10 равна 55.
Все задачи на сумму и разность четных и нечетных чисел можно решать с помощью подсчета сумм четных и нечетных чисел от заданного диапазона и дальнейшей арифметической операции.
Знание понятия «остаток» также может помочь в решении задач на сумму и разность чисел. Остаток — это число, оставшееся при делении одного числа на другое. Например, при делении 15 на 7 остаток равен 1.
При решении задач на сумму и разность чисел можно использовать остаток при делении на 2. Если число даёт остаток 0 при делении на 2, оно четное, в противном случае — нечетное.
Например, для решения задачи «Найдите произведение двух четных чисел» можно использовать остаток при делении на 2. Два четных числа дают остаток 0 при делении на 2. Произведение двух четных чисел также даст остаток 0 при делении на 2, что означает, что произведение также является четным числом.
Задачи на сумму и разность четных и нечетных чисел помогают закрепить знания о четных и нечетных числах, а использование остатка при делении на 2 позволяет упростить решение таких задач.
Остаток как инструмент при решении задач на распределение предметов и вещей
Понимание остатка в математике помогает решать различные задачи на распределение предметов и вещей между людьми или группами. Остаток — это количество, которое останется после того, как какое-то количество было поделено на определенную величину.
Допустим, у нас есть 16 мандаринов, и мы хотим разделить их поровну между 4 друзьями. Мы делим 16 на 4, и у нас получается остаток 0, что означает, что каждый друг получит по 4 мандарина.
Но что произойдет, если у нас будет 17 мандаринов? Если мы разделим их на 4, то у нас останется остаток 1. Это значит, что один из друзей получит на один мандарин больше, чем остальные.
Этот пример демонстрирует, как понимание остатка может быть полезным при решении задач на распределение предметов и вещей. Используя инструменты математики, мы можем рассчитать, сколько каждый человек получит и как распределить предметы наиболее справедливо.
Остаток — это важное понятие в математике, которое широко применяется в решении различных задач, таких как распределение предметов и вещей. Понимание этого понятия поможет ученикам успешно справляться с математическими задачами и научиться применять знания на практике.
Примеры задач на остаток в математике для 3 класса
Пример 1: В коробке лежит 28 яблок, а в ящике находится 10 коробок яблок. Сколько яблок останется в ящике, если из него вынуть две коробки?
Решение: Сначала найдем количество яблок в одной коробке — для этого нужно разделить 28 на 10, получим 2 ед. на одну коробку. Вынув две коробки, у нас останется 10 — 2 = 8 коробок. Значит, в ящике останется 8*2=16 яблок.
Пример 2: Мама испекла 30 пирожков и имеет 2 подноса по 12 ячеек. Сколько пирожков останется без подноса?
Решение: В каждом подносе 12 ячеек, а значит на двух подносах может поместиться 24 пирожка. Из всех 30 пирожков остается 30-24=6.
Пример 3: В аквариуме было 45 золотых и 25 серебряных рыбок. Несколько золотых и серебряных рыбок вытащили из аквариума и положили в новый рыбный круг. Оказалось, что в нем стало на 10 рыбок больше, чем было в аквариуме. Сколько золотых и серебряных рыбок вытащили из аквариума?
Решение: Пусть из аквариума было вытащено X золотых и Y серебряных рыбок. Тогда в новом круге стало (X+Y)+10 рыбок. С другой стороны, в аквариуме осталось (45-X)+(25-Y) рыбок, так как изначально было 45 золотых и 25 серебряных рыбок. Значит, у нас сейчас есть уравнение: (X+Y)+10=(45-X)+(25-Y). Решив его, получим, что X=20 и Y=5. Значит, из аквариума было вытащено 20 золотых и 5 серебряных рыбок.
Пример 4: В кино зал помещается 200 человек. На представлении было продано 140 билетов. Сколько мест осталось в зале?
Решение: Чтобы найти количество оставшихся мест, нужно вычесть количество проданных билетов из общего числа мест: 200-140=60. В зале осталось 60 свободных мест.
Пример 5: В магазине продали 2360 коробок конфет. На складе осталось еще 790 коробок. Сколько всего коробок конфет было на складе до продажи?
Решение: Чтобы найти количество коробок конфет до продажи, нужно сложить количество проданных коробок и количество оставшихся на складе: 2360+790=3150. Всего было 3150 коробок конфет на складе до продажи.
Остаток и работа со временем: задачи на время и часы
Работа со временем — один из самых распространенных вариантов применения остатка в математике. Решение задач на время и часы помогает развивать у детей не только математические навыки, но и компетенции в планировании и организации своего времени.
Например, задача: «в 7:30 было 300 мл воды в кувшине, а через каждые 15 минут мы добавляем еще 50 мл. Сколько будет воды в кувшине в 10:30?» Эта задача помогает научиться вычислять количество воды в кувшине на каждый отрезок времени с помощью деления с остатком и сложения, а также планировать свои действия во времени.
Другая задача на время и часы: «если мы вышли из дома в 8:15 и шли в школу 35 минут, то в какое время мы придем?» Задачи такого типа помогают научиться вычислять промежутки времени и использовать их для решения задач на конкретную дату или время. Также развиваются навыки планирования и оценки времени, необходимые для успешной организации дня.
Работа со временем и часами — это важные компетенции, которые помогают детям развивать логическое мышление, планирование и самоорганизацию. Решение задач с использованием остатка в математике помогает научиться решать задачи на время и часы не только в школе, но и в повседневной жизни.
Выводы о применении остатка в математике и его пользе для учеников
1. Остаток помогает понимать математические операции и связи между числами. Например, при делении чисел на цело остаток показывает, сколько останется после деления, и какие числа можно получить, если к заданному числу прибавить или отнять конкретное значение. Это помогает ученикам лучше понимать действия, которые происходят с числами и как они описываются.
2. Остаток полезен для решения задач и улучшения логического мышления. В задачах, связанных с делением чисел, ученики должны находить остаток, чтобы понять, какие числа можно получить при помощи математических операций. Это требует логического мышления, последовательности действий и аккуратности в работе. В результате решения задач ученики улучшают свои навыки в области логики и математического мышления.
3. Остаток продолжает использоваться в более продвинутых математических курсах. Он является основой для понимания смежных математических курсов, таких как алгебра и тригонометрия. Понимание концепции остатка в начальной школе является важным шагом для развития математических навыков и понимания различных математических операций и формул в более продвинутых курсах.
4. Остаток учит детей терпению и концентрации. Нахождение остатка требует от учеников терпения и концентрации, поскольку процесс требует внимания к деталям и связи между числами. Ученики должны быть готовы тратить время на решение проблем и уделять внимание подробностям, что может быть полезным для последующих математических занятий и школьной жизни в целом.
5. Остаток способствует развитию навыков самоконтроля и точности. Ученики должны быть внимательными при нахождении остатка, поскольку даже небольшая ошибка может привести к неправильному ответу. Это помогает детям развивать навыки самоконтроля, точности и аккуратности, что может быть полезным во многих аспектах школьной жизни.