Почему школьную математику иногда называют «элементарной геометрией 7»

Статья рассказывает о том, почему школьная математика включает элементарную геометрию и почему она обычно изучается в 7 классе. Вы узнаете, какие понятия из геометрии мы используем в повседневной жизни и почему они важны для математики.

Математика — один из самых важных и широко используемых предметов в школьной программе. В качестве первого уровня рассматривается элементарная геометрия, которую изучают в 7 классе. Но почему именно геометрию называют элементарной?

Основной причиной является то, что геометрия является первым курсом математики, который дети проходят в школе. Она знакомит школьников с базовыми понятиями, какие уже изученные в начальной школе, и даёт им понимание, как устроен мир. Геометрия помогает понимать свойства и взаимоотношения между фигурами и отношения между линиями, а также помогает развивать логическое мышление.

В процессе изучения элементарной геометрии школьники также изучают основы алгебры, которые используются для решения геометрических задач. Полученные знания помогают не только в школе, но и в жизни, например, при ремонте дома или установке мебели.

Таким образом, геометрия является важным шагом в учении математики и помогает школьникам получить базовые знания и навыки, необходимые для дальнейшего школьного образования.

Почему школьную математику называют элементарной геометрией 7: основы и причины

Школьная математика изучается начиная с первого класса и заканчивая выпускным экзаменом. Она является обязательным предметом для всех учеников и поэтому часто называется элементарной геометрией.

Основная причина такого названия заключается в том, что математика в школе уделяет большое внимание геометрии, которая также называется геометрией плоскости. В школьной программе геометрия является одним из основных разделов математики и изучается с первого по десятый класс.

Цель изучения геометрии в школе заключается в том, чтобы обучить учеников основам геометрии плоскости, теории пространственных фигур, аналитической геометрии и другие основы математики. Это позволяет в будущем легче изучать более сложные математические дисциплины, такие как алгебра и математический анализ.

Таким образом, школьная математика и геометрия являются основой для дальнейшего изучения математики и других наук. Именно поэтому ее называют элементарной геометрией. Кроме того, основы геометрии также применяются в повседневной жизни, в том числе при решении различных задач и при работе с компьютерной графикой.

Видео по теме:

Основные понятия

Геометрия — это отрасль математики, которая изучает пространственные фигуры, их свойства и взаимное расположение.

Геометрическая фигура — это замкнутая или незамкнутая плоская область, ограниченная линиями или кривыми.

Грань — это плоская поверхность, ограничивающая тело.

Угол — это взаимное расположение двух лучей, имеющих одну общую точку.

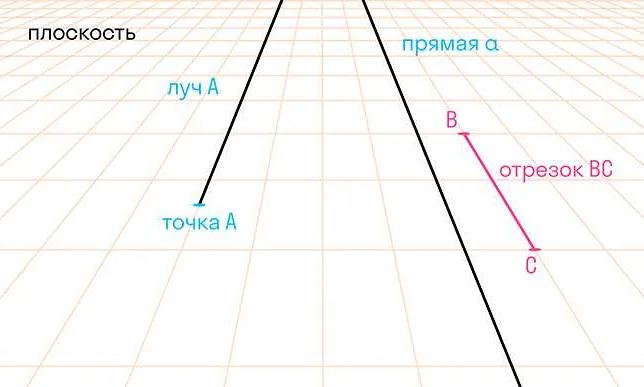
Луч — это прямая линия, исходящая из некоторой точки и не имеющая конца.

Отрезок — это часть прямой линии, между двумя её конечными точками.

Параллельные линии — это линии, которые всюду находятся на одинаковом расстоянии друг от друга и никогда не пересекаются.

Перпендикулярные линии — это линии, которые пересекаются под прямым углом.

Круг — это геометрическая фигура, которая образуется при вращении окружности вокруг её диаметра.

Площадь — это мера поверхности геометрической фигуры в квадратных единицах.

Объём — это мера трёхмерного пространства, занимаемого телом, выраженная в кубических единицах.

Теорема Пифагора — это одна из основных теорем в геометрии, которая устанавливает соотношение между длинами сторон прямоугольного треугольника: квадрат длины гипотенузы равен сумме квадратов длин катетов.

История возникновения геометрии

Геометрия — это одна из старейших наук, которая изучает форму, размеры, расположение и пространственное строение объектов. Ее истоки уходят в древнюю историю, когда люди начали заниматься измерением земли и строительством сооружений.

Первые записи о геометрии находятся в астрономической системе счета и измерения времени древних египтян в III тысячелетии до нашей эры. В дальнейшем геометрия развивалась в греческой цивилизации, благодаря работам Евклида, Пифагора и Аристотеля. Евклид создал известное произведение «Начала», которое по сей день является основополагающим учебником геометрии.

В средние века геометрия стала инструментом для выполнения различных строительных работ и измерений земли. В эпоху Возрождения геометрия вновь возродилась, а благодаря работам Ферма, Ньютона и Лейбница, она стала мощным инструментом математического анализа и расчетов.

Сегодня геометрия применяется во многих областях науки и техники, включая строительство, инженерию, архитектуру, информатику и теорию игр. Она является неотъемлемой частью образования и культуры человечества.

Объекты изучения элементарной геометрии

Геометрия — это наука, изучающая пространственные отношения и формы. Элементарная геометрия — это первый этап изучения геометрии в школе, который включает в себя основы планиметрии и стереометрии.

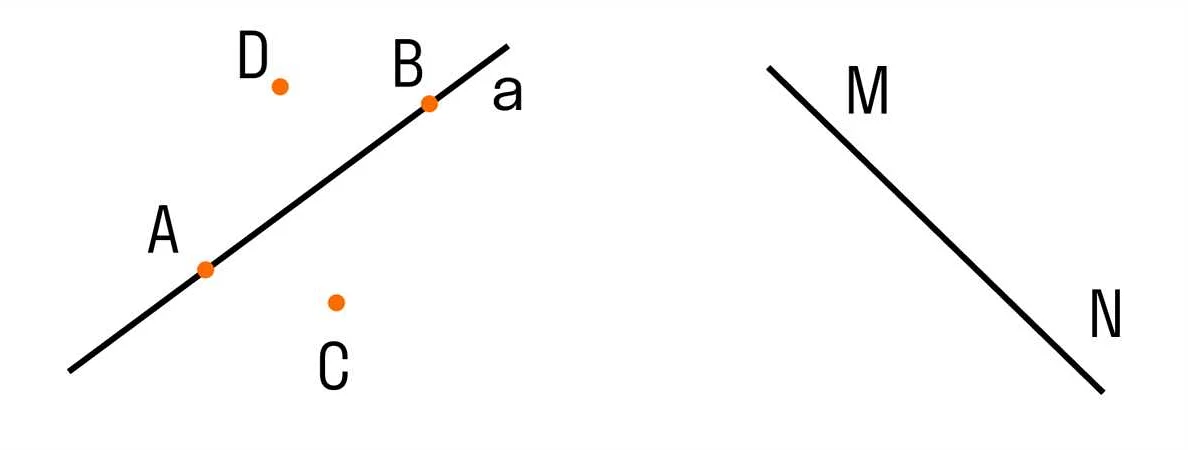
Основные объекты изучения элементарной геометрии — это точки, линии, плоскости, углы, многоугольники, окружности, треугольники и тела. Эти объекты являются базисом для понимания более сложных конструкций.

Точка — это самый простой объект в геометрии, который не имеет размеров и обозначается буквой. Линия — это множество бесконечных точек, которые расположены в пространстве в одном направлении. Плоскость — это множество точек, образующее плоскую поверхность без толщины.

Угол — это фигура, которая образуется двумя лучами, выходящими из одной точки, называемой вершиной. Многоугольник — это фигура, которая состоит из трех и более линий, закрывающих множество углов.

Окружность — это множество точек, которые расположены на одинаковом расстоянии от центра. Треугольник — это многоугольник, который состоит из трех линий. Тело — это трехмерный объект, который имеет длину, ширину и высоту.

Изучение этих объектов в элементарной геометрии позволяет развивать пространственное мышление и понимание геометрических закономерностей, использовать математический аппарат для решения задач и применять полученные знания в реальной жизни.

Принципы и методы геометрических исследований

Геометрические исследования являются важной частью математики и имеют широкое применение в реальной жизни, начиная от архитектуры и инженерии, до прикладной физики и географии.

Одним из основных принципов геометрических исследований является формулирование гипотез и доказательство их с использованием формальной логики и математических методов. В геометрическом исследовании часто используется метод описания свойств и фактов в терминах аксиом и теорем.

Еще одним принципом геометрических исследований является использование визуальных представлений, таких как диаграммы, графики и изображения, для облегчения восприятия информации и демонстрации связей между объектами.

Методы геометрических исследований включают в себя аналитический и синтетический подходы. Аналитический метод используется для изучения геометрических объектов и их свойств с использованием алгебраических и геометрических методов, таких как координатная геометрия и векторы. Синтетический метод использует геометрические построения и аксиоматические системы для изучения свойств геометрических объектов.

Важной частью методов геометрических исследований является решение геометрических задач, где требуется найти решение, используя геометрические свойства объектов. Эти методы могут включать использование теорем и правил, а также рассмотрение крайних случаев и аналогий с ранее решенными задачами.

Суммируя, геометрические исследования базируются на формализации свойств геометрических объектов, формулировании гипотез и доказательствах их, использовании визуальных представлений, а также аналитических и синтетических методов.

Современные направления развития геометрии

Современная геометрия включает в себя множество направлений. Одно из них – дифференциальная геометрия. Это раздел математики, который изучает свойства геометрических объектов в более высоких размерностях.

Другое направление – теория игр и топология. Топология изучает свойства геометрических объектов, которые не меняются при непрерывных преобразованиях. Теория игр, в свою очередь, изучает математические модели игр и их стратегии.

Также существуют разделы геометрии, которые занимаются исследованием симметрии и групп Ли. Геометрические трансформации и симметрии широко используются во многих сферах, включая физику и химию.

Важным направлением является компьютерная геометрия. Она занимается разработкой алгоритмов для решения геометрических задач и создания компьютерной графики. Компьютерная геометрия используется в различных областях, от проектирования до медицинских исследований.

Таким образом, геометрия продолжает оставаться важным разделом математики, и ее приложения охватывают множество областей. Развитие новых направлений и технологий открывает широкие возможности для исследований и применения геометрии в будущем.

Влияние геометрии на другие науки

Геометрия — одна из древнейших наук, которая изучает пространственные и фигурные свойства объектов. Благодаря своей универсальности и точности геометрия находит применение в других науках, помогая решать сложные задачи. Примерами могут служить:

• Физика — геометрия используется для описания и понимания движения тел, расположения в пространстве и рассчитывания оптических свойств материалов.
• Космология — геометрические принципы позволяют изучать гравитационные поля в космических объектах.
• Кристаллография — геометрия играет важную роль в определении структуры кристаллов и их свойств.
• География — геометрические принципы используются для определения формы Земли, расположения и формы ландшафтов, а также для создания карт и атласов.

Помимо перечисленных наук, геометрия находит применение в строительстве, проектировании и дизайне. Значительный вклад в развитие геометрии внесли именно эти отрасли, поскольку требуют точных расчетов и измерений.

Как геометрия помогает в повседневной жизни

Геометрия является одним из основных разделов математики и широко применяется в нашей повседневной жизни. Ее знание позволяет решать различные задачи и проблемы на работе, в учебе, дома и в других сферах жизни. Вот несколько примеров, как геометрия может пригодиться в повседневной жизни:

• Дизайн и строительство: Геометрия используется как в проектировании крупных строительных объектов, так и в дизайне пространства жилых помещений. Знание геометрии позволяет правильно выбирать пропорции, размеры и углы в интерьере и экстерьере.
• Финансы: Геометрические формулы используются в финансовых расчетах, таких как рассчитывание процентов, амортизационных выплат и других финансовых показателей.
• Навигация: Геометрия помогает в навигации по городу, на море и в воздухе. Карты, компасы, глобусы рассчитываются на основе геометрических принципов и формул.
• Кулинария: Геометрия используется при приготовлении блюд. Например, для вычисления объема емкости для порции теста для торта или венчика определенной формы.

Это только несколько примеров, как геометрия может помочь в повседневной жизни и применяется в различных областях жизни. Поэтому знание основ геометрии является необходимым навыком для каждого человека.

Примеры задач, решаемых при помощи геометрии

Геометрия используется для решения множества задач в различных областях. Она позволяет понимать и работать с пространственными формами и объектами. Ниже приведены некоторые области, в которых геометрия находит применение:

• Архитектура. Геометрия позволяет инженерам и архитекторам создавать планы, чертежи и модели проектов. Например, геометрия используется при проектировании зданий, мостов и дорог.
• Графика и дизайн. Геометрические принципы используются для создания иллюстраций, значков, логотипов, а также при оформлении интерьеров и экстерьеров.
• Физика. Геометрия и теория чисел играют важную роль в понимании законов физики, таких как закон сохранения энергии и закон сохранения импульса.
• Картография. Геометрические принципы используются при создании карт и глобусов, а также для измерения расстояний и определения географических координат.
• Байкинг. Геометрия применяется в измерении объема и формы различных продуктов, а также в создании декораций и оформлении кондитерских изделий.

Геометрические концепции помогают решать задачи, которые связаны с измерением и вычислением площадей, объемов и периметров. Например, геометрия помогает решать задачи вроде:

1. Найти площадь треугольника.
2. Рассчитать объем сферы.
3. Определить длину гипотенузы в прямоугольном треугольнике.
4. Найти длину окружности.
5. Рассчитать угол между двумя прямыми.

Кроме того, геометрия используется в технических и инженерных расчетах, для построения карт и моделей, а также в музыке и искусстве.

Почему геометрия является важным элементом образования

Геометрия — один из самых древних и фундаментальных разделов математики. Изучение геометрии начинается еще со школы, и это не случайно. Ведь геометрия помогает нам понимать пространственные отношения, строить и анализировать графики, планировать дороги и здания.

Геометрия важна также для развития мышления и логики. Решение геометрических задач требует не только знания теории, но и умение анализировать, строить логические цепочки и опираться на свои наблюдения и интуицию. Способность мыслить геометрически помогает нам решать не только математические задачи, но и повседневные проблемы.

Кроме того, геометрия является важным элементом подготовки к профессиям, связанным с наукой, техникой, архитектурой, дизайном и другими областями, где важен точный расчет и уверенное понимание пространственных отношений.

Изучение геометрии также способствует формированию способности абстрагироваться и видеть связи между вещами, что существенно для развития творческой личности и успешной жизни в обществе.

Какие профессии связаны с геометрией

Геометрия – это наука, изучающая форму, размер и свойства фигур, цифр и пространственных отношений. Так как геометрия присутствует в жизни каждого человека и используется в различных областях, многие профессии требуют знания геометрии.

Ниже приведены некоторые профессии, связанные с геометрией:

• Архитектор – проектирует здания, использует знания геометрии для расчета размеров и форм зданий, создает чертежи и модели;
• Инженер – разрабатывает, проектирует и строит инженерные сооружения, использует геометрические знания для расчета конструкций и определения прочности материалов;
• Дизайнер – работает с геометрическими формами и пропорциями при создании дизайнерских решений;
• Учитель математики – обучает учеников математике, включая геометрию;
• Врач – использует знания геометрии для расчета объемов органов и их расположения в теле человека;
• Геодезист – занимается измерением и созданием карт местности, использует знания геометрии для определения расстояний и углов;
• Механик – использует геометрию для создания точных инструментов и механизмов.

Целый ряд других профессий также использует геометрию, таких как художник, графический дизайнер, пилот и многие другие. Знание геометрии дает человеку возможность более точно понимать и моделировать окружающий мир.

Вопрос-ответ:

Почему математику в школе называют элементарной геометрией?

Прозвище «элементарная геометрия» получила школьная математика из-за основного направления изучения — планиметрической геометрии, которая занимается изучением фигур на плоскости, и не требует знания сложных математических понятий и формул.

Каковы основные причины изучения элементарной геометрии в школе?

Основная причина — это развитие логического мышления и умения использовать современные инструменты и технологии. Оно помогает развивать навыки абстрактного мышления, необходимого, чтобы быстро и легко осваивать новые знания. Кроме того, изучение геометрии способствует развитию способности к пространственному мышлению, которое полезно в повседневной жизни и профессиональной деятельности.

Можно ли обойтись без знания математики и элементарной геометрии в повседневной жизни?

В некоторых случаях можно, однако, знание математики и элементарной геометрии дают нам возможность решать повседневные задачи более точно и экономически выгодно, например, если мы хотим посчитать площадь стены перед покраской, или узнать к какой высоте поднялся шар, брошенный с крыши здания.

Какие навыки можно приобрести, изучая элементарную геометрию?

Изучая элементарную геометрию, можно научиться решать задачи, которые требуют логического мышления и пространственного воображения. Кроме того, она помогает совершенствовать навыки работы с геометрическими фигурами, что полезно в повседневной жизни и при решении профессиональных задач.

Какой математический курс считается продолжением изучения элементарной геометрии в школе?

После изучения элементарной геометрии в школе, ученики переходят к изучению алгебры, которая занимается изучением числовых выражений, уравнений и систем уравнений.

Почему многие школьники испытывают трудности при изучении элементарной геометрии?

Одна из основных причин трудностей в изучении элементарной геометрии состоит в том, что многие ученики не знают основ математики и попросту не умеют работать с формулами и понятиями. Кроме того, эта дисциплина требует хорошо развитого пространственного воображения и умения рассуждать логически, а не все ученики обладают этими навыками.

Зачем изучать геометрию, если в будущем я не буду работать в сфере науки или технологий?

Хотя умение решать геометрические задачи может быть необходимо только в определенных профессиях, навыки, приобретаемые при изучении элементарной геометрии, будут полезны в любой профессиональной деятельности. Они помогают узнавать шаблоны или правила в повседневных ситуациях, распознавать и устранять ошибки, анализировать данные и многое другое.