Что нужно повторить перед егэ по математике базовый уровень

Узнайте, какие темы и навыки нужно повторить перед сдачей экзамена по математике на базовом уровне ЕГЭ. Получите советы и рекомендации по подготовке к экзамену.

Единый государственный экзамен (ЕГЭ) по математике является одним из самых важных этапов в жизни старшеклассника. Успешное сдача этого экзамена открывает двери в вузы и предоставляет возможность выбирать желаемую профессию. Однако, подготовка к ЕГЭ требует времени, усилий и стратегического подхода.

В данной статье мы рассмотрим основные темы, которые следует изучать перед ЕГЭ по математике базового уровня. Материалы, которые будут рассмотрены, помогут вам обрести уверенность в своих знаниях и подготовиться к экзамену на высоком уровне.

Одной из ключевых тем, которая встречается на ЕГЭ по математике базового уровня, является алгебра. Важно освоить различные методы решения уравнений и неравенств, а также понять основы работы с функциями и графиками. Умение анализировать и применять алгебраические преобразования в решении задач является неотъемлемой частью успеха на экзамене.

Уверенное владение геометрией также является важным навыком для успешной сдачи ЕГЭ по математике. Понимание основных понятий и правил решения геометрических задач поможет вам справиться с любыми заданиями этой темы. Проанализируйте основные типы задач, которые могут встретиться на экзамене, и научитесь применять соответствующие формулы и методы решения.

Наконец, важно не забывать о вероятности и статистике. Эти темы также являются неотъемлемой частью экзамена по математике базового уровня. Изучите основные понятия и принципы вычисления вероятностей, а также научитесь анализировать и интерпретировать статистические данные. Тщательная подготовка к этим темам позволит вам успешно решать задачи на экзамене и получить высокий балл.

В целом, подготовка к ЕГЭ по математике базового уровня требует систематического подхода и практики. Изучите основные темы и методы решения задач, проводите время на решение практических заданий и принимайте участие в симуляционных экзаменах. Только так вы сможете достичь успеха и справиться с экзаменом на отлично!

Вводная часть

Основная цель сдачи ЕГЭ по математике – получение высокого балла, который будет учитываться при поступлении в вузы. Чем выше балл, тем больше возможностей открывается перед выпускником – выбор специальности, университета и даже страны для обучения за рубежом.

В данной статье мы рассмотрим основные темы, которые следует изучить перед сдачей ЕГЭ по математике базового уровня. Мы также расскажем о техниках подготовки, которые помогут вам успешно справиться с экзаменом.

Важность подготовки к ЕГЭ по математике базового уровня

Подготовка к ЕГЭ по математике базового уровня играет ключевую роль в достижении высоких результатов. Успех в этом экзамене требует от учеников не только знания математических концепций и умений, но и умения применять их на практике. Правильная подготовка помогает учащимся развить необходимые навыки, такие как аналитическое мышление, логика и решение сложных задач.

Подготовка к ЕГЭ по математике базового уровня также помогает снять стресс и тревожность, связанные с экзаменом. Чем лучше подготовлен ученик, тем увереннее он будет чувствовать себя во время экзамена, что может положительно сказаться на его результате.

Однако, подготовка к ЕГЭ по математике базового уровня требует времени и усилий. Регулярные занятия, самостоятельное изучение теории и практика решения задач позволят ученику улучшить свои навыки и повысить шансы на успешное сдачу экзамена.

В целом, подготовка к ЕГЭ по математике базового уровня является необходимым условием для достижения хороших результатов. Она дает ученикам возможность закрепить свои знания, развить необходимые навыки и повысить уверенность в себе, что важно как для успешной сдачи экзамена, так и для дальнейшего образования и карьеры.

Основные разделы подготовки

Подготовка к ЕГЭ по математике базового уровня включает в себя несколько основных разделов, которые необходимо изучить и усвоить перед экзаменом.

1. Алгебра. В этом разделе рассматриваются основные алгебраические операции, уравнения, неравенства, системы уравнений и неравенств, функции и их свойства.
2. Геометрия. Здесь изучаются геометрические фигуры, их свойства и характеристики, а также различные методы решения геометрических задач.
3. Теория вероятностей и математическая статистика. В этом разделе изучаются основные понятия и методы теории вероятностей, а также применение статистических методов для анализа данных.
4. Математическая логика и дискретная математика. Здесь рассматриваются основные понятия и методы математической логики, теории множеств, теории графов и комбинаторики.

Кроме того, для успешной подготовки к ЕГЭ по математике базового уровня необходимо много практиковаться, решая задачи различной сложности. Полезно также использовать специальные пособия и учебники, которые содержат теоретический материал и большое количество заданий для тренировки.

Важно помнить, что подготовка к ЕГЭ по математике базового уровня требует систематического и упорного труда. Регулярные занятия, разбитые на небольшие блоки материала, помогут улучшить понимание и запоминание материала, а также развить навыки решения задач.

Алгебра: основные темы и методы решения

Одной из основных тем алгебры является работа с алгебраическими выражениями. В этом случае необходимо уметь выполнять операции сложения, вычитания, умножения и деления с алгебраическими выражениями. Также важно уметь сокращать дроби и преобразовывать выражения разных видов.

Еще одной темой алгебры является решение уравнений и неравенств. Здесь требуется умение находить корни уравнений и решать неравенства с неизвестными значениями. Для решения задач в этой области необходимо знать различные методы решения и применять их в зависимости от вида уравнения или неравенства.

Также в алгебре важным является работа с функциями. Необходимо уметь определять область определения и область значений функций, строить и анализировать графики функций, находить значения функций в заданных точках и решать уравнения, содержащие функции.

ТемаМетоды решения

Алгебраические выражения	Операции со сложными выражениями, преобразование выражений
Уравнения и неравенства	Методы решения: подстановка, перенос, приведение к каноническому виду
Функции	Определение области определения и области значений функций, построение графиков, решение уравнений с функциями

Важно уделять достаточно времени изучению каждой из этих тем и отрабатывать навыки решения задач. Помимо этого, необходимо регулярно тренироваться на выполнение тестовых заданий, чтобы привыкнуть к формату ЕГЭ и научиться решать задачи в ограниченное время.

Итак, основные темы алгебры в программе подготовки к ЕГЭ по математике базового уровня включают работу с алгебраическими выражениями, решение уравнений и неравенств, а также работу с функциями. Отличное владение этими темами и методами решения задач позволит успешно справиться с экзаменом и получить высокий балл.

Геометрия: главные темы и стратегии решения задач

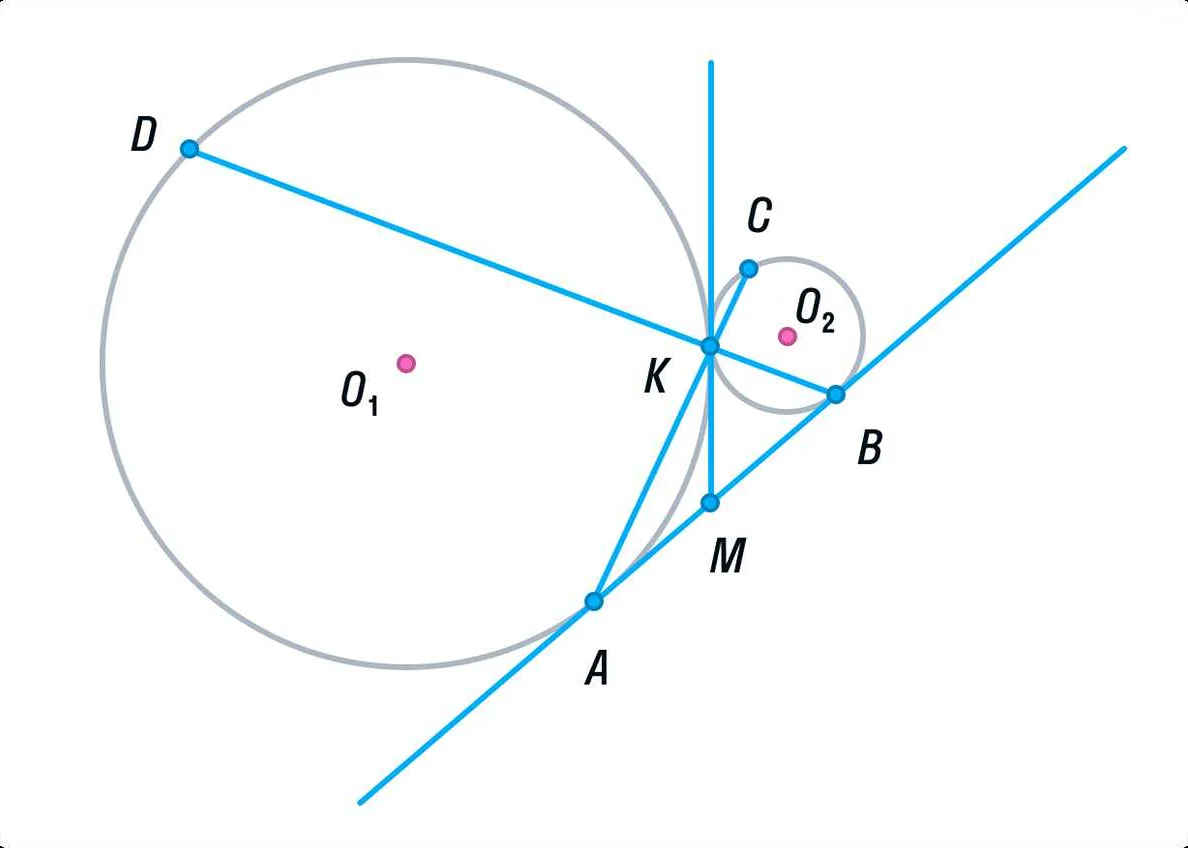
Одной из главных тем геометрии на ЕГЭ является треугольник. Знание его свойств, формул и теорем позволяет успешно решать задачи, связанные с треугольниками. Например, задачи на нахождение площади, периметра, высот, медиан и других характеристик треугольника.

Важной темой геометрии является также круг. Знание основных формул и теорем, связанных с кругом, позволяет решать задачи на нахождение его радиуса, длины окружности, площади круга.

Некоторые другие главные темы геометрии на ЕГЭ включают в себя прямоугольник, квадрат, параллелограмм, трапецию, прямоугольный треугольник и окружность. Знание свойств, формул и теорем по этим фигурам также является необходимым для успешного решения задач.

Основной стратегией решения геометрических задач на ЕГЭ является анализ условия задачи и построение дополнительных геометрических построений, которые позволят свести задачу к более простой форме. Также важно знать основные теоремы и свойства геометрических фигур, чтобы применять их в процессе решения задачи.

Итак, геометрия является важной темой на ЕГЭ по математике базового уровня. Понимание основных тем и стратегий решения задач в геометрии позволит успешно справиться с этим разделом экзамена и получить высокий балл.

Теория вероятностей и статистика: ключевые понятия и подходы

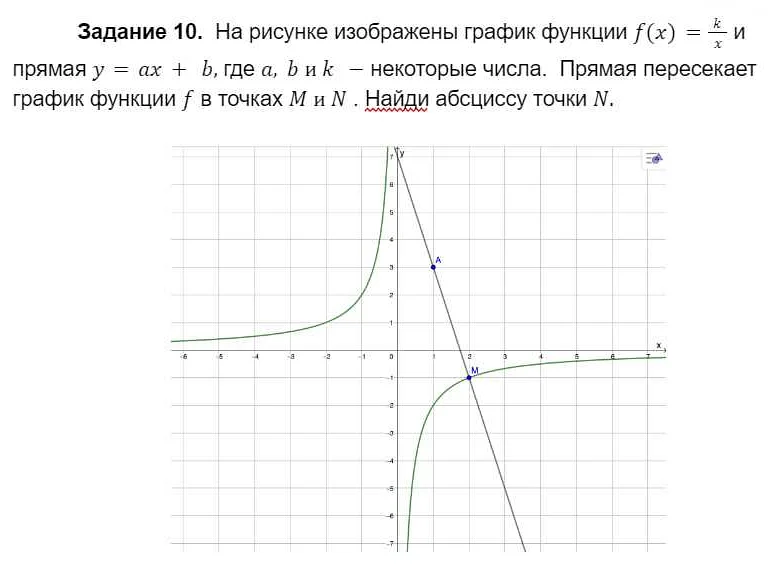
Вероятность — это мера того, насколько событие возможно или вероятно. Она измеряется числом от 0 до 1, где 0 означает невозможность события, а 1 — его полную уверенность.

Случайная величина — это функция, которая сопоставляет каждому исходу случайного эксперимента числовое значение. Она может быть дискретной, принимающей только определенные значения, или непрерывной, принимающей любое значение из определенного диапазона.

Распределение вероятностей — это функция, которая определяет вероятность появления каждого возможного значения случайной величины. Оно может быть описано с помощью таблицы, графика или математической формулы.

Математическое ожидание — это среднее значение случайной величины, учитывающее вероятности ее возможных значений. Оно вычисляется умножением каждого значения на его вероятность и сложением результатов.

Дисперсия — это мера разброса значений случайной величины относительно ее математического ожидания. Она вычисляется суммой квадратов разностей значений от среднего значения, умноженных на вероятности.

Выборка — это подмножество из генеральной совокупности, которое используется для получения информации и делает возможным статистические выводы о генеральной совокупности.

Статистика — это наука, которая изучает сбор, анализ, интерпретацию и представление данных. Она использует математические методы и модели для извлечения информации из данных и принятия статистических выводов.

Гипотеза — это предположение о связи между переменными, которое проверяется на основе данных. Гипотезы могут быть принятыми или отвергнутыми на основе статистического анализа.

В данном разделе мы ознакомились с основными понятиями и подходами в теории вероятностей и статистике. Эти знания будут полезны при решении задач и анализе данных на ЕГЭ по математике базового уровня.

Математическая логика: принципы и типы задач

Принципы математической логики основаны на идее формализации и строгой логической структуре. Основной принцип — это принцип исключенного третьего, который гласит, что любое высказывание либо истинно, либо ложно, без третьего варианта. Также в математической логике используются принципы конъюнкции (логическое И) и дизъюнкции (логическое ИЛИ), а также отрицания (логическое НЕ).

В задачах математической логики часто используются таблицы истинности, которые позволяют определить значения логических выражений в зависимости от значений истинности их компонентов. Задачи могут быть связаны с доказательством истинности высказываний, построением логических цепочек рассуждений или определением логических связей между высказываниями.

Типы задач, связанных с математической логикой, могут включать задачи на определение пропозиций, выполнение логических операций, составление таблиц истинности, построение логических цепочек, решение задач на логическое следование и вывод.

Подготовка к ЕГЭ по математике базового уровня включает изучение основ математической логики, в том числе основных принципов и методов решения задач. Правильное понимание и применение математической логики поможет учащимся успешно справиться с заданиями ЕГЭ и достичь высоких результатов.

Тригонометрия: основные функции и применение в задачах

Основными тригонометрическими функциями являются синус, косинус и тангенс. Синус угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе. Тангенс угла равен отношению противоположного катета к прилежащему катету.

Тригонометрические функции широко применяются в задачах, связанных с измерением углов и расчетами в различных областях науки, техники и естественных наук. Например, используя тригонометрические функции, можно рассчитать высоту башни, не имея возможности измерить ее напрямую. Также тригонометрия используется в геодезии, физике, астрономии и других научных дисциплинах.

В задачах ЕГЭ по математике базового уровня часто встречаются задачи, требующие применения тригонометрических функций. Важно уметь правильно сформулировать задачу, построить треугольник и применить соответствующую тригонометрическую функцию для решения задачи.

Успешная подготовка к ЕГЭ по математике базового уровня требует от ученика глубокого понимания основных тригонометрических функций и умения применять их в различных задачах. Правильное использование тригонометрических функций позволит решать задачи более эффективно и точно, что поможет достичь хороших результатов на экзамене.

Аналитическая геометрия: координаты, уравнения и связанные задачи

Один из основных инструментов аналитической геометрии – это система координат. В двумерном пространстве используется декартова система координат, состоящая из двух взаимно перпендикулярных осей – оси абсцисс (Ox) и оси ординат (Oy). Каждая точка в этой системе задается упорядоченной парой чисел (x, y), где x – это координата по оси абсцисс, а y – по оси ординат.

Уравнения могут использоваться для описания геометрических объектов на плоскости. Например, уравнение прямой в декартовой системе координат имеет вид y = kx + b, где k – наклон прямой, а b – ее смещение по вертикальной оси. С помощью такого уравнения можно определить координаты точек, принадлежащих прямой, а также провести график этой прямой на плоскости.

Аналитическая геометрия также включает в себя решение задач, связанных с геометрическими фигурами. Например, задачи на пересечение прямых или нахождение расстояния между точками. Для решения таких задач необходимо применять знания координат и уравнений.

Изучение аналитической геометрии позволяет увидеть связь между алгеброй и геометрией, а также развить навыки работы с координатами и уравнениями. Это очень полезный навык при решении задач по математике и может быть полезен не только в школьном курсе, но и в дальнейшей профессиональной деятельности.

Математический анализ: основные концепции и методы решения

Основной концепцией математического анализа является предел функции. Предел функции определяет, как функция ведет себя вблизи определенной точки или в бесконечности. Он позволяет определить, насколько близко значение функции может быть к определенному числу.

Методы решения задач в математическом анализе включают такие понятия, как производная и интеграл. Производная функции определяет ее скорость изменения в каждой точке. Она позволяет решать задачи оптимизации, находить экстремумы функций и анализировать их поведение. Интеграл функции, в свою очередь, определяет площадь под кривой и позволяет решать задачи, связанные с накоплением и суммированием.

Основные методы решения задач математического анализа включают использование формул и свойств функций, применение правил дифференцирования и интегрирования, а также использование геометрических и графических методов. Для успешной подготовки к ЕГЭ по математике базового уровня необходимо усвоить эти методы и научиться их применять для решения различных задач.

Важно отметить, что математический анализ является одной из наиболее сложных и объемных тем на ЕГЭ по математике. Поэтому регулярная тренировка и практика решения задач являются основными компонентами успешной подготовки к этому разделу экзамена. Стратегия успешного решения задач включает в себя четкое понимание теоретических концепций, правильный подход к анализу и решению задач, а также умение применять полученные знания на практике.

Видео по теме:

Какие основные темы нужно изучать для подготовки к ЕГЭ по математике базового уровня?

Для успешной подготовки к ЕГЭ по математике базового уровня необходимо изучить следующие основные темы: алгебраические выражения и уравнения, функции и графики, системы линейных уравнений, геометрия, вероятность и статистика.

Какие техники помогут справиться с заданиями ЕГЭ по математике базового уровня?

Для успешного выполнения заданий ЕГЭ по математике базового уровня рекомендуется использовать следующие техники: четкое формулирование условий задачи, систематическое решение заданий, использование графических методов, проверка ответов, а также умение работать с графическим калькулятором.

Какие сложности могут возникнуть при подготовке к ЕГЭ по математике базового уровня?

При подготовке к ЕГЭ по математике базового уровня могут возникнуть сложности в понимании математических понятий и алгоритмов, в решении сложных задач, в умении работать с графическим калькулятором. Также могут возникнуть трудности в организации учебного процесса и в распределении времени на подготовку к разным темам.

Какую литературу можно использовать для подготовки к ЕГЭ по математике базового уровня?

Для подготовки к ЕГЭ по математике базового уровня можно использовать учебники по математике для 10-11 классов, пособия по подготовке к ЕГЭ, сборники заданий и тестов, а также интерактивные ресурсы и онлайн-курсы.

Какую роль играет практика в подготовке к ЕГЭ по математике базового уровня?

Практика является очень важным элементом подготовки к ЕГЭ по математике базового уровня. Она помогает отработать навыки решения задач разных типов, улучшить скорость выполнения заданий, а также повысить уверенность в своих знаниях и умениях. Рекомендуется регулярно решать задания из разных источников и анализировать ошибки.

Какие основные темы должен знать ученик для успешной подготовки к ЕГЭ по математике базового уровня?

Для успешной подготовки к ЕГЭ по математике базового уровня ученик должен знать основные темы, такие как: алгебраические операции, уравнения и неравенства, системы уравнений, пропорции и проценты, функции, графики функций, геометрия (в том числе планиметрия и стереометрия), тригонометрия, комбинаторика и вероятность. Важно уделить время каждой из этих тем и научиться решать задачи, связанные с ними.