Что нужно знать для сдачи егэ по математике профильный уровень

Узнайте ключевые аспекты и стратегии для успешной сдачи ЕГЭ по математике на профильном уровне. Откройте секреты подготовки, полезные советы и рекомендации от экспертов, чтобы достичь высоких результатов на этом важном экзамене.

Единый государственный экзамен (ЕГЭ) по математике является одним из важнейших испытаний для абитуриентов, которые планируют поступать в вузы. Профильный уровень ЕГЭ по математике предназначен для тех, кто выбирает технические и естественнонаучные специальности. Подготовка к этому экзамену требует серьезного и систематического подхода, а также глубоких знаний в математике.

В программе ЕГЭ по математике профильного уровня содержатся различные разделы: алгебра, геометрия, математический анализ и статистика. Каждый из этих разделов имеет свои особенности и специфику. Подготовка к экзамену включает в себя изучение теоретического материала, решение практических задач, а также проведение самостоятельных тренировок.

Одним из ключевых аспектов подготовки к ЕГЭ по математике является умение анализировать и решать сложные задачи. Экзамен требует не только знания формул и алгоритмов, но и умение применять их на практике. Поэтому рекомендуется регулярно выполнять задания различного уровня сложности, чтобы развить навык анализа и применения математических знаний.

Кроме того, для успешной подготовки к ЕГЭ по математике профильного уровня важно уметь работать с графиками, таблицами и формулами. Это поможет вам быстро и точно анализировать информацию и находить необходимые решения. Также рекомендуется использовать различные учебные пособия, интернет-ресурсы и обучающие программы, которые помогут вам систематизировать и углубить свои знания в математике.

Наконец, не забывайте о регулярной самопроверке и контроле знаний. Решайте тесты и задания, анализируйте свои ошибки и работайте над их исправлением. Только так вы сможете максимально эффективно подготовиться к ЕГЭ по математике профильного уровня и достичь высоких результатов.

Вводный курс для подготовки к ЕГЭ по математике профильный уровень

Подготовка к ЕГЭ по математике профильный уровень требует усиленного изучения основных тем и задач этого предмета. В данном вводном курсе мы рассмотрим основные темы, которые необходимо знать для успешной подготовки и сдачи экзамена.

• Алгебра и аналитическая геометрия. В этой части курса рассматриваются основные понятия алгебры и геометрии, включая работу с уравнениями, неравенствами, функциями, системами уравнений и преобразованиями графиков.
• Геометрия. В данном разделе курса изучаются основные геометрические фигуры и их свойства, а также решение задач на нахождение площадей, объемов и углов.
• Тригонометрия. В этой части курса рассматриваются основные тригонометрические функции, их свойства и применение в решении задач.
• Вероятность и статистика. В данном разделе курса изучаются основные понятия вероятности и статистики, а также методы решения задач на их основе.
• Математический анализ. В этой части курса рассматриваются основные понятия математического анализа, такие как пределы, производные и интегралы, а также их применение в решении задач.

Вся материальная часть курса сопровождается примерами и задачами для закрепления полученных знаний. Постепенное изучение и практика по решению задач помогут укрепить навыки и подготовиться к успешной сдаче ЕГЭ по математике на профильном уровне.

Основные темы и разделы математики

Алгебра:

1. Рациональные числа
2. Степени и корни
3. Линейные уравнения и неравенства
4. Квадратные уравнения и неравенства
5. Системы линейных уравнений
6. Функции и графики
7. Последовательности и ряды
8. Матрицы и определители
9. Комплексные числа

Геометрия:

1. Основные понятия геометрии
2. Треугольники
3. Четырехугольники
4. Площади фигур
5. Правильные многогранники
6. Тригонометрия
7. Планиметрия
8. Стереометрия
9. Преобразования плоскости и пространства

Математический анализ:

1. Последовательности и пределы
2. Функции и их свойства
3. Дифференциальное исчисление
4. Интегральное исчисление
5. Дифференциальные уравнения
6. Ряды и их сходимость

Вероятность и статистика:

1. Вероятность событий
2. Случайные величины
3. Распределения случайных величин
4. Математическая статистика

Дискретная математика:

1. Множества и операции над ними
2. Теория графов
3. Теория чисел
4. Комбинаторика
5. Логика и алгебра логики

Математическая логика и методы доказательств:

1. Методы доказательств
2. Теория множеств
3. Математическая индукция
4. Математическое рассуждение
5. Теория вероятностей

Другие темы:

1. Компьютерная математика
2. Математическая физика
3. Математическая экономика
4. Дифференциальные уравнения в частных производных
5. Теория управления
6. Криптография

Примеры типовых заданий и их решения

Задание 1:

Найдите корни квадратного уравнения: x2 — 6x + 9 = 0.

Решение:

Для решения данного квадратного уравнения можно воспользоваться формулой дискриминанта:

D = b2 — 4ac

где a, b и c — коэффициенты уравнения.

В данном случае:

a = 1, b = -6 и c = 9.

Вычислим дискриминант:

D = (-6)2 — 4 * 1 * 9 = 36 — 36 = 0

Так как дискриминант равен нулю, уравнение имеет один корень:

x = -b/2a = -(-6)/2 * 1 = 3

Ответ: корень уравнения x = 3.

Задание 2:

Решите систему уравнений:

{

2x — 3y = 5

x + y = 1

}

Решение:

Мы можем решить данную систему уравнений методом подстановки.

Из второго уравнения выразим x: x = 1 — y.

Подставим это значение в первое уравнение:

2(1 — y) — 3y = 5

2 — 2y — 3y = 5

-5y = 3

y = -3/5

Теперь найдем x из второго уравнения:

x = 1 — y = 1 — (-3/5) = 1 + 3/5 = 8/5

Ответ: x = 8/5 и y = -3/5.

Алгебра и арифметика

Арифметика изучает основные операции над числами: сложение, вычитание, умножение и деление. Также в арифметике изучаются различные системы счисления, десятичные дроби, проценты, пропорции и другие базовые математические понятия.

Алгебра занимается изучением алгебраических выражений, уравнений, неравенств, функций и графиков. В алгебре используются различные операции, такие как сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.

Во время подготовки к ЕГЭ по математике профильного уровня необходимо усвоить основные понятия алгебры и арифметики, а также научиться применять их в решении различных задач. Важно понимать логику и принципы этих разделов математики, чтобы успешно справиться с экзаменом.

В рамках подготовки к ЕГЭ по математике профильного уровня стоит познакомиться с основными темами алгебры и арифметики, такими как уравнения, неравенства, системы уравнений и неравенств, функции, графики функций, пропорции, проценты, десятичные дроби и другие. Уделите внимание решению задач и практике, чтобы укрепить свои знания и навыки.

Раздел «Алгебра и арифметика» является одним из основных разделов программы ЕГЭ по математике профильного уровня. Он включает в себя множество тем и концепций, которые необходимо усвоить для успешного сдачи экзамена. Постепенное изучение и практика по этому разделу помогут вам подготовиться к ЕГЭ и достигнуть высоких результатов.

Геометрия и теория чисел

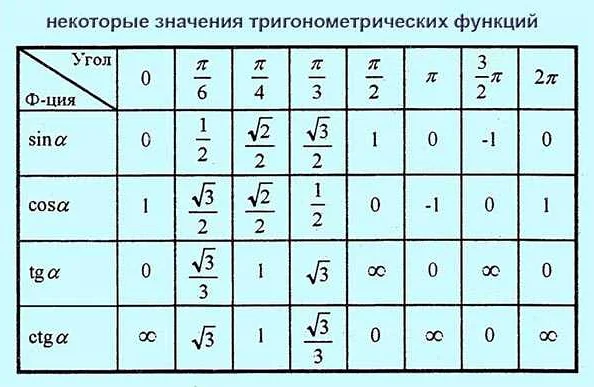
В геометрии важно знать основные геометрические фигуры, их свойства и взаимосвязи. Нужно уметь находить периметр, площадь и объем различных фигур, а также решать задачи на их нахождение. Также важно знать основные теоремы и правила геометрии: теоремы Пифагора, Талеса, синусов и косинусов, а также правила подобия и равенства треугольников.

В теории чисел необходимо знать основные понятия и методы работы с числами. Важно уметь разложить число на простые множители, найти наибольший общий делитель и наименьшее общее кратное. Также нужно знать свойства чисел, например, свойства четных и нечетных чисел, свойства делимости и простых чисел.

В этом разделе ЕГЭ по математике профильного уровня обычно встречаются задачи, требующие применения геометрических и числовых знаний. Важно понимать, как применять эти знания для решения задач и уметь проводить логические рассуждения.

Темы геометрии и теории чиселПримеры задач

Геометрические фигуры и свойства	Найти площадь треугольника, зная его высоту
Теоремы и правила геометрии	Доказать, что треугольник является прямоугольным
Разложение чисел на множители	Найти все простые делители числа 36
Свойства чисел	Доказать, что сумма двух четных чисел является четным числом

Чтобы успешно справиться с заданиями по геометрии и теории чисел, необходимо хорошо знать теоретический материал и уметь применять его на практике. Рекомендуется решать много различных задач и тренироваться в логическом мышлении.

Таблицы и графики

Таблицы представляют собой упорядоченный набор данных, разделенный на строки и столбцы. Они часто используются для организации и представления числовых значений, фактов или информации. Таблицы могут быть простыми или сложными, в зависимости от количества переменных и степени детализации.

Графики, с другой стороны, позволяют визуально представить данные в виде точек, линий, столбцов или других геометрических фигур. Они помогают исследователям и аналитикам видеть и понимать закономерности, тренды и взаимосвязи между данными. Графики бывают разных типов, таких как линейные, столбчатые, круговые и т. д.

При подготовке к ЕГЭ по математике профильный уровень, необходимо уметь читать и анализировать таблицы и графики, а также использовать их для решения задач. Необходимо знать основные типы графиков и таблиц, уметь определить зависимости и тренды по данным, а также уметь проводить интерполяцию и экстраполяцию данных.

Статистика и вероятность

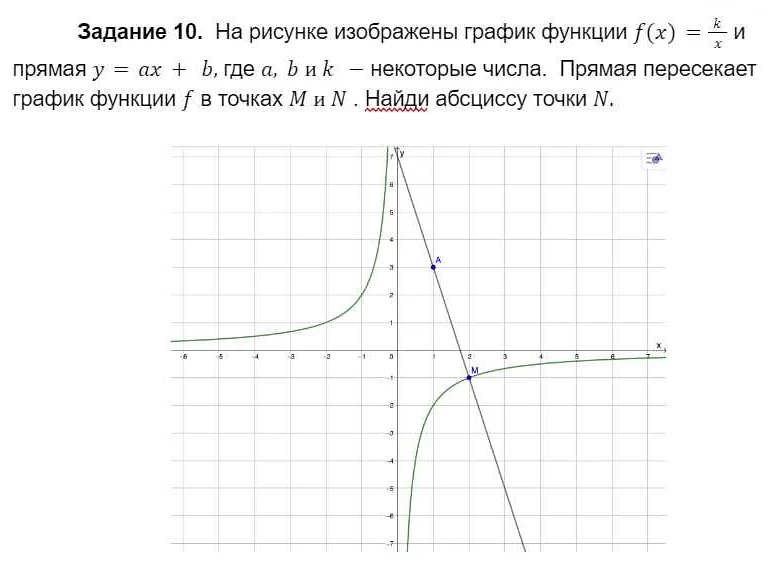
В статистике обычно используются различные методы сбора данных, такие как опросы, эксперименты и наблюдения. Затем полученные данные анализируются и интерпретируются с помощью различных статистических методов, таких как среднее значение, медиана, мода и корреляция.

Вероятность изучает случайные события и их вероятность. Вероятность события определяется как отношение числа благоприятных исходов к общему числу возможных исходов. Она может быть выражена в виде десятичной дроби, процента или отношения.

Важно знать основные понятия и формулы, связанные со статистикой и вероятностью, чтобы успешно решать задачи. Например, стандартное отклонение, выборочное среднее, зависимые и независимые события — все это важные понятия, которые пригодятся при решении задач на ЕГЭ.

ПонятиеОписание

Стандартное отклонение	Мера разброса значений вокруг среднего значения
Выборочное среднее	Среднее значение наблюдаемых данных
Зависимые события	События, которые влияют друг на друга
Независимые события	События, которые не влияют друг на друга

Знание статистики и вероятности поможет вам не только на ЕГЭ, но и в повседневной жизни. Вы сможете анализировать данные, прогнозировать результаты и принимать обоснованные решения на основе вероятностных моделей.

Теория функций и дифференциальные уравнения

Теория функций изучает свойства математических функций, их графики и основные операции с функциями. Основные типы функций, которые необходимо знать, включают линейные функции, квадратичные функции, показательные и логарифмические функции. Для каждого типа функции важно знать их графики, особенности поведения и способы решения уравнений с их участием.

Дифференциальные уравнения являются уравнениями, содержащими производные. Они используются для моделирования различных явлений в физике, экономике, биологии и других науках. Знание дифференциальных уравнений позволяет решать задачи на определение функций, удовлетворяющих определенным условиям. Основные типы дифференциальных уравнений, которые нужно знать, включают линейные дифференциальные уравнения первого порядка, уравнения в полных дифференциалах и уравнения с разделяющимися переменными.

Для успешной подготовки к ЕГЭ по математике профильный уровень необходимо уделить достаточно времени изучению теории функций и дифференциальных уравнений. Помимо теоретических знаний, также важно научиться решать задачи на применение этих знаний. Решение множества задач из разных областей позволит закрепить материал и улучшить навыки решения задач с использованием функций и дифференциальных уравнений.

Основные понятияПримеры функцийТипы дифференциальных уравнений

Линейные функции	y = 3x + 5	Линейные дифференциальные уравнения первого порядка
Квадратичные функции	y = x^2 + 2x + 1	Уравнения в полных дифференциалах
Показательные функции	y = e^x	Уравнения с разделяющимися переменными
Логарифмические функции	y = ln(x)

Практические рекомендации и советы по подготовке

Подготовка к ЕГЭ по математике на профильном уровне требует систематического и упорного труда. Вот несколько практических рекомендаций, которые помогут вам эффективно использовать свое время и достичь успеха:

1. Организуйте свое время. Разбейте свой учебный процесс на небольшие ежедневные задания и придерживайтесь определенного расписания. Это поможет вам регулярно повторять и укреплять материал, а также снизит стресс перед экзаменом.

2. Постепенно повышайте уровень сложности задач. Начните с простых упражнений и постепенно переходите к более сложным. Это поможет вам укрепить основы и развить навыки решения сложных задач.

3. Практикуйтесь в решении типовых заданий. Изучите структуру и особенности каждого типа задания, и решайте их в большом количестве. Знание особенностей каждого типа задания поможет вам быстро и точно решать задачи во время экзамена.

4. Работайте над ошибками. Анализируйте свои ошибки и старайтесь понять, почему вы совершили их. Это поможет вам избегать повторения ошибок и улучшать свои навыки.

5. Не забывайте о теории. Регулярно повторяйте основы математики, чтобы сохранить свои знания на должном уровне. Помимо решения задач, изучайте теорию и разбирайте примеры из учебника или дополнительной литературы.

6. Сотрудничайте с другими учащимися. Обсуждайте задачи с одноклассниками или товарищами по учебе. Взаимное обучение и обмен опытом помогут вам лучше понять материал и найти новые подходы к решению задач.

7. Занимайтесь физическими упражнениями и поддерживайте здоровый образ жизни. Физическая активность поможет вам сохранять хорошую концентрацию и выносливость во время подготовки и экзамена.

Следуя этим практическим рекомендациям, вы сможете эффективно подготовиться к ЕГЭ по математике профильного уровня и достичь хорошего результата.

Видео по теме:

Какой профильный уровень ЕГЭ по математике существует и что нужно знать для его сдачи?

ЕГЭ по математике имеет два профильных уровня: базовый и профильный. Для сдачи ЕГЭ по профильному уровню необходимо знать все материалы базового уровня, а также дополнительные темы, которые указаны в программе. Важно обратить внимание на геометрические задачи, задачи на комбинаторику и задачи на преобразование уравнений.

Какие особенности есть у профильного уровня ЕГЭ по математике?

Особенности профильного уровня ЕГЭ по математике заключаются в том, что задания более сложные по сравнению с базовым уровнем. Они требуют умения анализировать и решать сложные математические проблемы. Также в заданиях профильного уровня часто встречаются задачи, в которых нужно применять знания из разных разделов математики.

Какие основные темы нужно знать для успешной подготовки к ЕГЭ по математике профильный уровень?

Для успешной подготовки к ЕГЭ по математике профильный уровень необходимо хорошо знать такие основные темы, как алгебраические выражения и уравнения, системы уравнений, функции и графики функций, геометрические фигуры и пространства, комбинаторика и вероятность. Эти темы являются основой для дальнейшего изучения математики и позволяют решать разнообразные задачи на экзамене.

Какие навыки нужно развивать для успешной подготовки к ЕГЭ по математике профильный уровень?

Для успешной подготовки к ЕГЭ по математике профильный уровень необходимо развивать навыки анализа задач, умение применять математические знания на практике, умение строить логические цепочки решения задач, умение работать с графиками и табличными данными, умение решать задачи на время и контролировать свою работу. Также важно развивать навыки самостоятельной работы, умение находить информацию в учебниках и справочных материалах, умение формулировать и аргументировать свои решения.

Какие ресурсы и материалы можно использовать для подготовки к ЕГЭ по математике профильный уровень?

Для подготовки к ЕГЭ по математике профильный уровень можно использовать различные ресурсы и материалы. Наиболее полезными могут быть учебники по математике для подготовки к ЕГЭ, пособия с разбором типовых заданий, задач и тестов, интерактивные программы и приложения для тренировки навыков решения задач, онлайн-курсы и видеоуроки по математике, примеры реальных заданий из предыдущих экзаменов, сайты с задачами и тестами по математике, а также консультации и занятия с преподавателями по математике. Важно выбрать те ресурсы и материалы, которые наиболее подходят для вашего уровня и стиля обучения.