Что такое последовательность в математике

Последовательность в математике — это упорядоченный набор элементов, расположенных в определенном порядке. Она может быть конечной или бесконечной, и каждый элемент последовательности имеет свой номер или индекс. Последовательности широко используются в математике для изучения различных свойств и моделей, и они играют важную роль в анализе, алгебре и других областях математики.

В математике последовательность — это упорядоченный набор чисел или элементов, в котором каждый элемент имеет определенное положение относительно предыдущих и последующих элементов. Понятие последовательности является одним из основных понятий в анализе и алгебре, играющее важную роль в решении различных задач и проблем.

Последовательности можно классифицировать по различным признакам. Наиболее распространенные типы последовательностей включают арифметическую, геометрическую и рекуррентную. Арифметическая последовательность — это последовательность, в которой каждый следующий элемент получается прибавлением к предыдущему элементу одного и того же числа, называемого разностью. Геометрическая последовательность — это последовательность, в которой каждый следующий элемент получается умножением предыдущего элемента на одно и то же число, называемое знаменателем. Рекуррентная последовательность — это последовательность, в которой каждый элемент определяется с помощью предыдущих элементов с помощью некоторого правила или формулы.

Примеры последовательностей могут быть найдены в различных областях математики и физики. Например, арифметическая последовательность может представлять числовую прогрессию, где каждый элемент увеличивается на одно и то же число. Геометрическая последовательность может представлять геометрическую прогрессию, где каждый элемент получается умножением предыдущего элемента на одно и то же число. Рекуррентная последовательность может представлять последовательность Фибоначчи, где каждый элемент определяется суммой двух предыдущих элементов.

Последовательности являются важным инструментом в математике и используются для моделирования и анализа различных явлений и процессов. Они позволяют нам лучше понять и изучить закономерности и свойства числовых последовательностей, а также применять их в решении реальных проблем и задач.

Что такое последовательность в математике?

Последовательности используются в математике для изучения свойств числовых рядов, пределов, геометрических фигур и многих других объектов. С их помощью можно изучать различные закономерности и осуществлять анализ различных моделей.

Существует несколько типов последовательностей, включая арифметические, геометрические и рекуррентные последовательности. Арифметическая последовательность представляет собой последовательность, в которой каждый следующий член получается путем прибавления одной и той же константы к предыдущему члену. Геометрическая последовательность представляет собой последовательность, в которой каждый следующий член получается путем умножения предыдущего члена на одну и ту же константу. Рекуррентная последовательность имеет определенное правило, с помощью которого можно вычислить любой член последовательности через предыдущие члены.

Примеры последовательностей в математике могут быть следующими: арифметическая последовательность {2, 5, 8, 11, 14, …}, где каждый следующий член получается путем добавления 3 к предыдущему члену; геометрическая последовательность {2, 6, 18, 54, 162, …}, где каждый следующий член получается путем умножения предыдущего члена на 3; и рекуррентная последовательность Фибоначчи {0, 1, 1, 2, 3, 5, 8, 13, …}, где каждый следующий член получается путем сложения двух предыдущих членов.

Определение и основные понятия

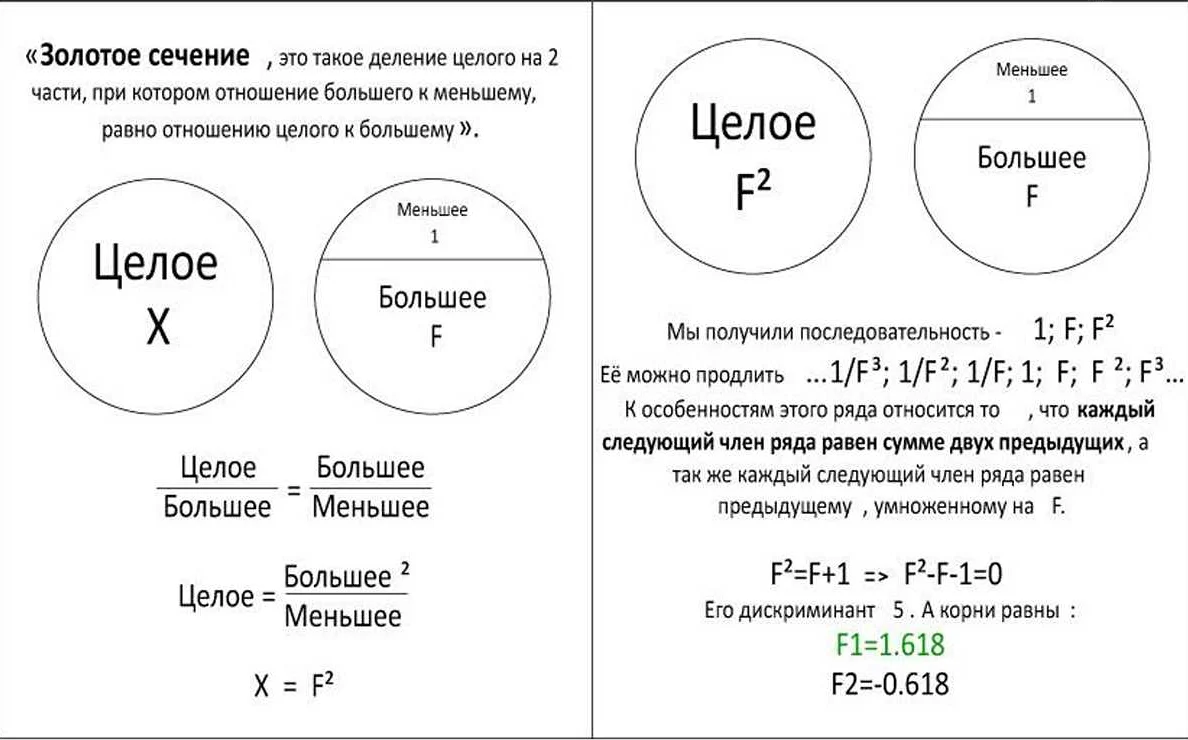
Последовательность может быть конечной или бесконечной. Конечная последовательность содержит только конечное количество элементов, например, последовательность чисел 1, 2, 3, 4, 5. Бесконечная последовательность имеет бесконечное количество элементов, например, последовательность натуральных чисел 1, 2, 3, 4, …

Типы последовательностей зависят от элементов, из которых они состоят. Некоторые основные типы последовательностей включают арифметическую и геометрическую последовательности.

Арифметическая последовательность — это последовательность, в которой каждый следующий элемент получается прибавлением одного и того же числа, называемого разностью, к предыдущему элементу. Например, последовательность 2, 5, 8, 11, 14 является арифметической с разностью 3.

Геометрическая последовательность — это последовательность, в которой каждый следующий элемент получается умножением предыдущего элемента на одно и то же число, называемое знаменателем. Например, последовательность 2, 6, 18, 54 является геометрической с знаменателем 3.

Последовательности играют важную роль в математике, физике, информатике и других науках. Они используются для описания и решения различных задач, а также для разработки алгоритмов и моделей.

ТерминОписание

Последовательность	Упорядоченный набор элементов, следующих друг за другом в определенном порядке.
Конечная последовательность	Последовательность с конечным количеством элементов.
Бесконечная последовательность	Последовательность с бесконечным количеством элементов.
Арифметическая последовательность	Последовательность, в которой каждый следующий элемент получается прибавлением разности к предыдущему элементу.
Геометрическая последовательность	Последовательность, в которой каждый следующий элемент получается умножением знаменателя на предыдущий элемент.

Типы последовательностей

В математике существует несколько типов последовательностей, каждый из которых имеет свои особенности и свойства. Ниже приведены основные типы последовательностей:

ТипОписание

Арифметическая последовательность	Последовательность, в которой каждый следующий элемент получается путем добавления к предыдущему одного и того же числа, называемого разностью. Например, 2, 5, 8, 11, 14…
Геометрическая последовательность	Последовательность, в которой каждый следующий элемент получается путем умножения предыдущего элемента на одно и то же число, называемое знаменателем. Например, 2, 6, 18, 54, 162…
Рекуррентная последовательность	Последовательность, в которой каждый следующий элемент зависит от одного или более предыдущих элементов. Например, последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, 13…
Арифметико-геометрическая последовательность	Последовательность, в которой каждый следующий элемент получается как сумма арифметической и геометрической прогрессий. Например, 1, 3, 7, 13, 21, 31…

Каждый из этих типов последовательностей имеет свои специфические свойства, которые могут быть использованы для исследования и анализа различных математических моделей и задач.

Арифметическая последовательность

Разность арифметической последовательности обозначается буквой d. Если первый элемент последовательности равен a1, то каждый следующий элемент можно выразить формулой:

an = a1 + (n — 1) * d,

где n — номер элемента последовательности.

Пример арифметической последовательности:

1. Разность (d) = 3
2. Первый элемент (a1) = 2
3. Второй элемент (a2) = 2 + (2 — 1) * 3 = 5
4. Третий элемент (a3) = 2 + (3 — 1) * 3 = 8
5. Четвертый элемент (a4) = 2 + (4 — 1) * 3 = 11
6. Пятый элемент (a5) = 2 + (5 — 1) * 3 = 14

В данном примере разность арифметической последовательности равна 3, а первый элемент равен 2. Каждый следующий элемент получается путем увеличения предыдущего элемента на 3.

Геометрическая последовательность

Формула общего члена геометрической последовательности:

an = a1 * rn-1

где an — n-ый член последовательности, a1 — первый член последовательности, r — знаменатель, n — номер члена последовательности.

Примеры геометрической последовательности:

1. 1, 2, 4, 8, 16, 32, … — каждый следующий член получается умножением предыдущего члена на 2.
2. 3, 6, 12, 24, 48, 96, … — каждый следующий член получается умножением предыдущего члена на 2.
3. -5, 10, -20, 40, -80, … — каждый следующий член получается умножением предыдущего члена на -2.

Формула общего члена

Формула общего члена может быть разной в зависимости от типа последовательности. Например, для арифметической последовательности формула общего члена будет иметь вид:

• an = a1 + (n — 1)d, где an — n-ый член последовательности, a1 — первый член последовательности, d — разность между соседними членами.

Для геометрической последовательности формула общего члена будет иметь вид:

• an = a1 * r^(n — 1), где an — n-ый член последовательности, a1 — первый член последовательности, r — знаменатель пропорциональной прогрессии.

Зная формулу общего члена, мы можем легко вычислить любой член последовательности, что позволяет нам проводить различные операции и исследования над последовательностями в математике.

Рекуррентная последовательность

Общая формула для рекуррентной последовательности имеет вид:

an = f(an-1, an-2, …, an-k)

где an — n-й элемент последовательности, f — функция, определяющая зависимость элементов от предыдущих, и k — количество предыдущих элементов, участвующих в определении следующего элемента.

Рекуррентные последовательности широко применяются в различных областях математики, физики, компьютерных наук и других дисциплин. Они позволяют описывать сложные и упорядоченные процессы, моделировать поведение систем и решать различные задачи.

Примеры рекуррентных последовательностей:

• Последовательность Фибоначчи: an = an-1 + an-2, где a0 = 0, a1 = 1.
• Последовательность простых чисел: an = an-1 + 1, где a0 = 2.
• Последовательность Пелла: an = 2an-1 + an-2, где a0 = 0, a1 = 1.

Изучение рекуррентных последовательностей позволяет развить навыки анализа и обработки данных, а также применять их для решения различных задач и вычислений.

Примеры последовательностей

В математике существует множество различных типов последовательностей. Вот некоторые из них:

• Арифметическая последовательность: {2, 5, 8, 11, 14, …}
• Геометрическая последовательность: {1, 2, 4, 8, 16, …}
• Фибоначчиева последовательность: {0, 1, 1, 2, 3, 5, 8, 13, …}
• Последовательность простых чисел: {2, 3, 5, 7, 11, 13, 17, 19, …}
• Последовательность квадратных чисел: {1, 4, 9, 16, 25, …}

Это лишь некоторые примеры последовательностей, которые могут встречаться в математике. Каждая из них имеет свои особенности и может быть использована для решения различных задач.

Применение последовательностей в математике и реальной жизни

Одним из примеров использования последовательностей в математике является решение задач на арифметическую и геометрическую прогрессии. Например, в экономике последовательности используются для моделирования роста или убывания цен на товары, для прогнозирования спроса и предложения, а также для определения оптимальных стратегий в бизнесе.

В физике последовательности применяются для описания временных рядов, например, при изучении движения тела или изменения физических параметров в пространстве. Они помогают установить закономерности и предсказать будущие значения.

В статистике последовательности используются для анализа данных и проверки гипотез. Например, при исследовании влияния различных факторов на результаты эксперимента или определении закономерностей в поведении случайных процессов.

Кроме того, последовательности находят применение в компьютерных науках, в особенности при разработке алгоритмов сортировки и поиска данных, а также в криптографии для создания шифровальных алгоритмов.

Таким образом, понимание и применение последовательностей позволяет решать различные задачи, связанные с анализом данных, прогнозированием, моделированием и оптимизацией процессов в математике и реальной жизни.

Вопрос-ответ:

Что такое последовательность в математике?

Последовательность в математике — это упорядоченная коллекция элементов, где каждый элемент определен в соответствии с некоторым правилом или закономерностью.

Какие бывают типы последовательностей в математике?

В математике существует несколько типов последовательностей, включая арифметическую последовательность, геометрическую последовательность, фибоначчиеву последовательность и т.д.

Чем отличается арифметическая последовательность от геометрической?

Арифметическая последовательность является последовательностью, в которой каждый следующий элемент получается путем прибавления одного и того же числа (называемого разностью) к предыдущему элементу. Геометрическая последовательность, в свою очередь, получается путем умножения каждого элемента на одно и то же число (называемое знаменателем).

Какие примеры последовательностей можно привести?

Примерами последовательностей могут служить арифметическая последовательность чисел 1, 4, 7, 10, 13, 16 и геометрическая последовательность чисел 2, 6, 18, 54, 162, 486.

Зачем нужны последовательности в математике?

Последовательности в математике используются для изучения различных моделей и закономерностей, а также для решения задач из различных областей науки, экономики и физики.

Что такое последовательность в математике?

Последовательность в математике — это набор чисел, записанных в определенном порядке. Каждое число в последовательности называется элементом, и они следуют друг за другом в определенной последовательности.

Какие типы последовательностей существуют в математике?

В математике существует несколько типов последовательностей. Одним из наиболее распространенных типов являются арифметические последовательности, где каждый следующий элемент получается прибавлением фиксированного числа (шага) к предыдущему элементу. Еще одним типом последовательности являются геометрические последовательности, где каждый следующий элемент получается умножением предыдущего элемента на фиксированное число (знаменатель). Кроме того, существуют также фибоначчиевы последовательности, последовательности Фарея и другие.

Видео по теме: