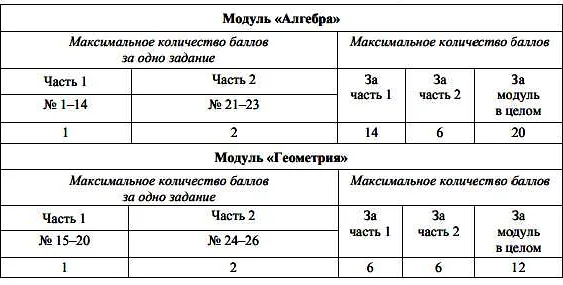
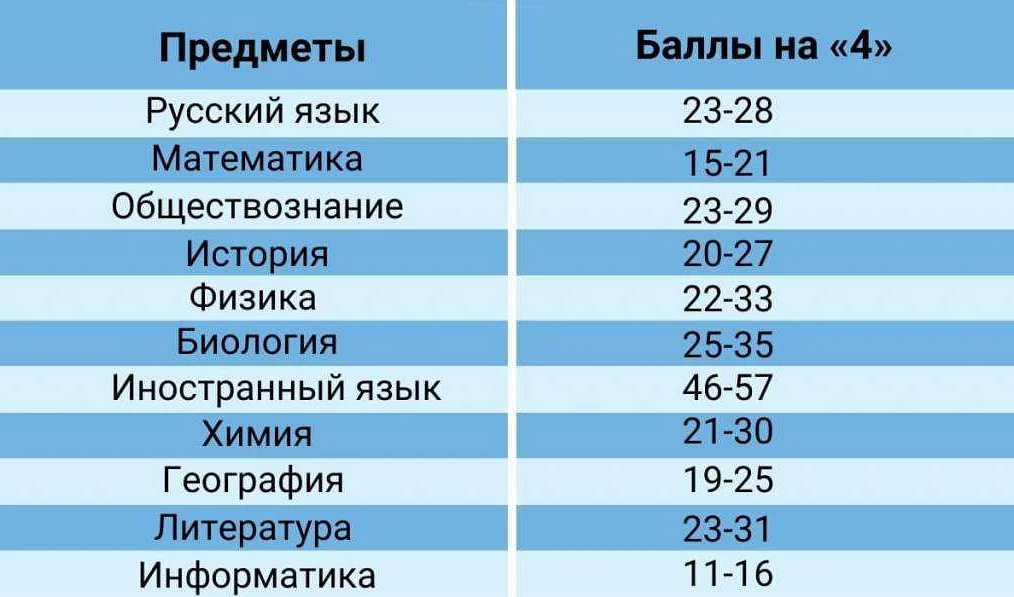
Как успешно решать задачи по геометрии в ОГЭ по математике: советы и примеры

Узнайте, как эффективно решать задачи по геометрии в ОГЭ по математике: какие формулы и правила необходимо знать, как правильно подходить к решению задачи и как избежать распространенных ошибок. Подготовьтесь к экзамену и получите максимальный результат с помощью наших советов и рекомендаций.

ОГЭ по математике – это важный этап для всех школьников, которые хотят успешно поступить в вуз. Одним из трудных разделов этого экзамена является геометрия, вызывающая беспокойство и страх у многих учеников. К счастью, с помощью некоторых практических советов и стратегий вы можете стать увереннее в решении задач по геометрии, что заметно повысит вашу успеваемость и улучшит шансы на успешный экзамен.

Хорошее владение геометрическими фигурами и условиями задач – это важный инструмент для решения задач по геометрии. Убедитесь, что вы знакомы с терминологией и определениями, связанными с углами, лицами, сторонами и другими элементами геометрических фигур. Это поможет вам лучше понимать условия задач и использовать правильные термины в решении задач.

Для успешного решения задач по геометрии очень важно уметь визуализировать геометрические фигуры и условия задачи на бумаге. При решении задач по геометрии на ОГЭ помните, что существует множество способов изобразить фигуры и условия задачи на бумаге. Выберите то, что лучше всего соответствует задаче и позволяет вам видеть все необходимые элементы графического решения.

Подготовка к решению задач

Правильная подготовка к решению задач по геометрии является важной частью успешной сдачи ОГЭ по математике. В этом разделе мы расскажем о нескольких стратегиях, которые помогут вам подготовиться к решению геометрических задач.

1. Понимайте теоремы и определения

Перед тем, как приступить к решению задач, важно хорошо знать теоремы и определения геометрии. Обратите особое внимание на теоремы, которые относятся к углам, прямолинейным и параллельным линиям, а также на определения геометрических фигур.

2. Рисуйте схемы

При решении геометрических задач очень важно нарисовать схему, которая поможет вам лучше понять условие задачи и выбрать правильное решение. Рисуйте все линии, углы и отметки, которые указаны в условии задачи.

3. Разбирайте типовые задачи

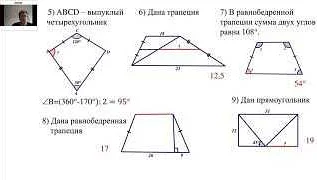
На ОГЭ часто встречаются типовые задачи, которые имеют определенный алгоритм решения. Изучите эти задачи заранее и разбейте их на небольшие шаги. Это поможет вам быстрее решать задачи на экзамене и не запутаться в условиях.

4. Надежные формулы

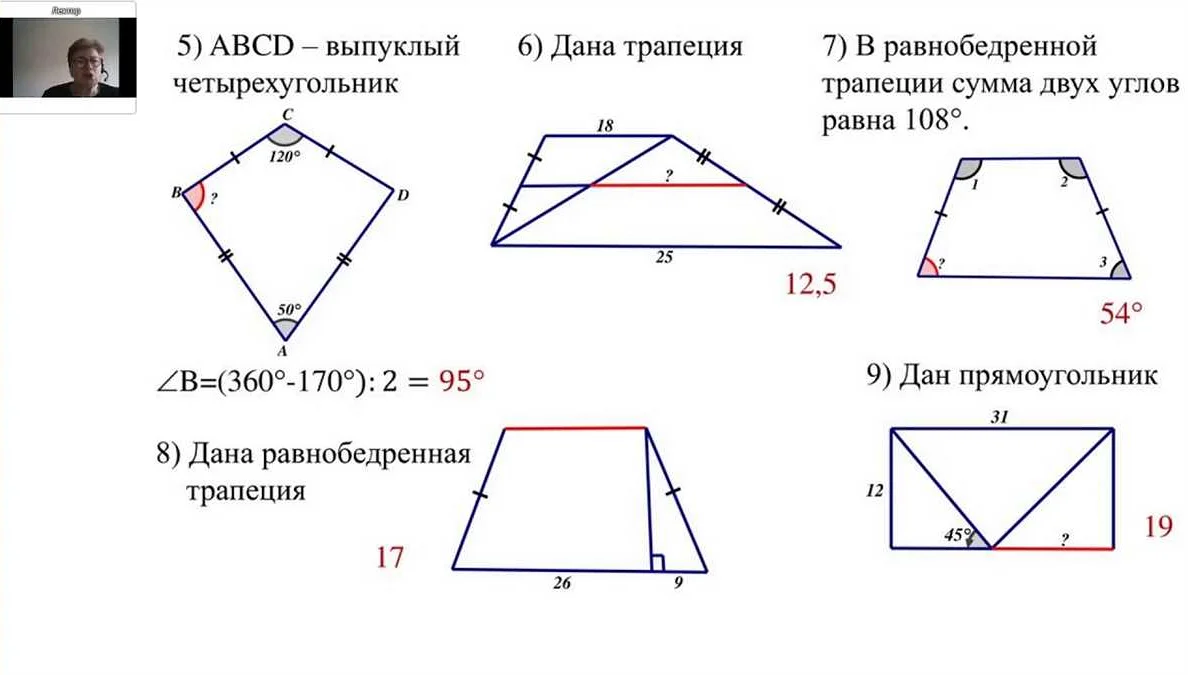
При решении задач по геометрии часто используются формулы для расчета площади, периметра и объема фигур. Важно знать все формулы заранее, чтобы не тратить время на их поиск на экзамене.

Соответствующая подготовка к сдаче заданий ГИА по математике может быть очень эффективной и существенно улучшить итоговый результат.

Видео по теме:

Изучение свойств геометрических фигур

Для успешного решения задач по геометрии в ОГЭ необходимо уметь определять различные свойства геометрических фигур. Одна из основных задач — определение типа фигуры по её характеристикам.

Например, треугольник можно классифицировать по длинам его сторон и углам между ними. Различные типы треугольников — прямоугольные, тупоугольные и остроугольные — обладают разными свойствами, которые можно использовать при решении задач.

Круг — это фигура, которая происходит из окружности. Он имеет радиус, диаметр и центр. Круг может быть использован для определения площади, длины окружности и других свойств.

Важно понимать также, что некоторые геометрические фигуры — квадрат, прямоугольник, параллелограмм — являются частными случаями более общих классов фигур. Например, прямоугольник — это частный случай параллелограмма, у которого все углы прямые. Это знание может помочь при решении задач, если недостаточно информации для определения типа фигуры точно.

• Стоит отметить, что знание свойств геометрических фигур является необходимым, но недостаточным условием для успешного решения задач по геометрии.
• Часто задачи могут содержать неожиданные и нестандартные решения, поэтому наряду с изучением теории, важная роль отводится и тренировке абстрактного мышления.
• Регулярная практика решения задач поможет улучшить умение оперировать свойствами геометрических фигур и повысить шансы на успешный результат при ОГЭ.

Разбор типовых задач на нахождение периметра и площади

Задача №1: Найти периметр и площадь прямоугольника со сторонами 8 см и 12 см.

Решение: Периметр прямоугольника равен сумме длин его сторон, то есть 2 * (8 см + 12 см) = 40 см. Площадь прямоугольника равна произведению длины и ширины, то есть 8 см * 12 см = 96 кв. см.

Задача №2: Найти периметр и площадь квадрата со стороной 6 см.

Решение: Периметр квадрата равен 4 * (6 см) = 24 см. Площадь квадрата равна сторона в квадрате, то есть (6 см) * (6 см) = 36 кв. см.

Задача №3: Найти периметр и площадь треугольника со сторонами 5 см, 7 см и 10 см.

Решение: Периметр треугольника равен сумме длин его сторон, то есть 5 см + 7 см + 10 см = 22 см. Для нахождения площади треугольника можно воспользоваться формулой Герона:

S = √p(p — a)(p — b)(p — c), где p = (a + b + c)/2

В данном случае p = (5 см + 7 см + 10 см)/2 = 11 см

S = √11(11 — 5)(11 — 7)(11 — 10) = √11 * 6 * 4 * 1 = 12 кв. см

Задача №4: Найти периметр и площадь ромба со стороной 6 см и углом 60° между сторонами.

Решение: Периметр ромба равен 4 * (6 см) = 24 см. Для нахождения площади ромба нужно перемножить длину диагоналей и разделить на 2:

S = (d1 * d2)/2, где d1 и d2 — диагонали ромба

Так как угол между сторонами ромба 60°, то диагонали ромба равны:

d1 = 2 * (6 см * sin 60°/2) = 2 * (6 см * 0.87/2) = 5.22 см,

d2 = 2 * (6 см * cos 60°/2) = 2 * (6 см * 0.5/2) = 3 см.

Следовательно, S = (5.22 см * 3 см)/2 = 7.83 кв. см.

Вопрос-ответ:

Какие общие тактики можно использовать для решения задач по геометрии в ОГЭ по математике?

Перед началом решения задач по геометрии важно четко представлять себе картинку и структуру фигуры. Затем, следует применять основные геометрические теоремы, такие как теорема Пифагора, равенство треугольников, соотношения между сторонами и углами треугольника и т.д. Важно также обращать внимание на подобные треугольники и пропорции между сторонами. Наконец, необходимо понимать, как решать задачи на построение геометрических фигур.

Какие типы задач по геометрии бывают на ОГЭ по математике?

Можно выделить несколько типов задач: задачи на расчет длин сторон и углов геометрических фигур, задачи на построение геометрических фигур, задачи на вычисление площадей и объемов, задачи на применение теорем и свойств геометрических фигур.

Как решать задачи на построение геометрических фигур?

Перед началом построения важно понять условия задачи, например, длину или угол, который необходимо построить. Затем, нужно использовать свойства геометрических фигур, чтобы определить, какие линии необходимо провести и какие углы необходимо построить. В конце, нужно проверить, что построение удовлетворяет всем условиям задачи и выполнить дополнительные действия, например, найти площадь фигуры.

Как найти площадь треугольника?

Формула для нахождения площади треугольника — это S=(a*h)/2, где a — длина одной из сторон, а h — высота, опущенная на эту сторону. Если высота неизвестна, то ее можно найти, используя теорему Пифагора или равенство треугольников.

Как найти длину стороны в прямоугольном треугольнике?

Для нахождения длины стороны прямоугольного треугольника можно воспользоваться теоремой Пифагора: c²=a²+b², где c — гипотенуза, а и b — катеты. Для нахождения катета может быть переписана как a или b = квадратный корень(c²-б²).

Как определить, являются ли два треугольника подобными?

Два треугольника считаются подобными, если соотношение их сторон пропорционально друг другу. Можно также использовать свойство соответствующих углов — если углы между соответствующими сторонами двух треугольников равны, то эти треугольники подобны.

Как найти объем куба?

Объем куба вычисляется по формуле V=a³, где a — длина ребра куба. Для нахождения длины ребра можно использовать информацию о площади грани, если такая информация предоставлена в условии задачи.

Решение задач на соотношение между сторонами

Для решения задач на соотношение между сторонами треугольника необходимо в первую очередь выявить данные о сторонах, углах или высотах треугольника. После этого можно применить соответствующие теоремы и формулы для вычисления соотношений между сторонами.

Одной из самых известных теорем на соотношение между сторонами является теорема синусов. Ее формула гласит:

sin α/a = sin β/b = sin γ/c

где α, β, γ – углы треугольника, а, b, с – соответствующие стороны.

Если известны две стороны и угол между ними, можно использовать теорему косинусов:

c^2 = a^2 + b^2 — 2ab cos γ

где c – третья сторона треугольника, a и b – известные стороны, γ – угол между ними.

Для решения задач на соотношение высот треугольника используют теорему о высотах:

a1/a2 = c2/c1

где a1 и a2 – высоты, проведенные к основаниям c1 и c2 соответственно.

Важно помнить, что для применения этих формул необходимо знать значение углов и/или сторон треугольника. При решении задач на соотношение между сторонами треугольника не забывайте выводить ответ с необходимой точностью и указывать единицы измерения.

Решение задач на нахождение высоты и биссектрисы

Решение задач на нахождение высоты и биссектрисы треугольника включает в себя использование базовых геометрических знаний и формул. Рассмотрим на примере задачу:

Пример задачи: В треугольнике ABC проведены высота AH и биссектриса BL. Известно, что AB=8, BC=10, AC=6. Найдите AH и BL.

Решение:

1. Найдем площадь треугольника ABC по формуле Герона. Для этого нужно найти полупериметр треугольника, который равен (AB+BC+AC)/2=12. Вычисляем площадь треугольника по формуле Герона: √(12(12-8)(12-10)(12-6))= 24.
2. Найдем высоту треугольника, проведенную к основанию AB. Для этого воспользуемся формулой площади треугольника: S=0.5*AB*AH. Подставляем значения, получаем: AH=2S/AB=48/8=6.
3. Найдем биссектрису угла B. Для этого воспользуемся формулой: BL=2*sqrt(AC*BC*p*(p-AB))/(BC+AC), где p – полупериметр треугольника. Подставляем значения, получаем: BL=8.

Таким образом, ответом на задачу являются длины высоты AH, равной 6, и биссектрисы угла B, равной 8.

Знание формул и базовых алгоритмов позволит решать задачи на нахождение высот и биссектрис треугольников в ОГЭ по математике.

Решение задач на касательные и радикальные оси

В задачах на касательные и радикальные оси нужно использовать знания о том, как устроена окружность, ее радиус и диаметр. Также нужно иметь понимание о том, что касательная — это прямая, касающаяся окружности в точке пересечения. Радикальная ось — это прямая, на которой лежат касательные, проведенные к окружности.

Чтобы решить задачу на касательные и радикальные оси, нужно сначала найти уравнение окружности, которая дана в условии. Это позволит найти ее радиус и диаметр. Затем нужно использовать свойства радикальных осей и касательных, чтобы найти нужные величины.

Если задача находится в координатной плоскости, то можно использовать уравнение окружности в виде (x-a)^2+(y-b)^2=r^2, где (a, b) — координаты центра окружности, r — радиус. Если задача не находится в координатной плоскости, то можно использовать геометрическую конструкцию, чтобы найти уравнение окружности.

Если в условии задачи дана радикальная ось, нужно найти ее уравнение. Обычно это просто прямая, перпендикулярная радиусу окружности и проходящая через центр окружности. Далее нужно найти точки пересечения радикальной оси с окружностью и длину отрезка между этими точками. В задачах на касательные нужно найти точку касания касательной с окружностью и использовать ее для решения задачи.

Важно помнить, что в задачах на касательные и радикальные оси нужно использовать знания о том, как устроена окружность, ее радиус и диаметр, а также свойства касательных и радикальных осей. Правильно примененные знания помогут легко и быстро решить задачу.

Решение задач на подобие и гомотетию

Задачи на подобие и гомотетию встречаются довольно часто в ОГЭ по математике. Чтобы успешно решать такие задачи, необходимо знать определения и правила подобия и гомотетии.

Подобные фигуры – это фигуры, которые имеют одинаковые формы, но разные размеры. Для того, чтобы убедиться в подобии двух фигур, необходимо проверить, что их соответствующие углы равны, а соответствующие отрезки имеют одинаковые пропорции.

Гомотетия – это преобразование, при котором фигура увеличивается или уменьшается в заданную число раз. Для того, чтобы убедиться в гомотетии двух фигур, необходимо проверить, что их центры гомотетии лежат на одной прямой, а соответствующие отрезки имеют одинаковые пропорции.

Как правило, в задачах на подобие и гомотетию требуется найти длину некоторого отрезка или площадь фигур. Для решения таких задач необходимо использовать основные формулы подобия и гомотетии.

Если фигуры подобны, то отношение длин соответствующих сторон равно коэффициенту подобия, а отношение площадей равно квадрату этого коэффициента.

Якорными точками в задачах на гомотетию обычно являются центр гомотетии и его одна из точек. Если даны соответствующие стороны двух подобных фигур, то коэффициент гомотетии может быть найден как отношение длин этих сторон.

Важно понимать, что при решении задач на подобие и гомотетию необходимо быть внимательным и аккуратным. Ошибки в расчетах могут привести к неверному ответу.

Решение задач, связанных с кругами

В задачах, связанных с кругами, необходимо уметь работать с радиусом, диаметром, центром и дугой круга. Основой решения задач являются формулы, связанные с этими элементами.

К примеру, если известен диаметр круга, то радиус можно вычислить по формуле: R = D/2. Если известен радиус, то диаметр вычисляется как: D = 2R. Также можно вычислить длину окружности по формуле: L = 2πR, где π равно 3,14 (в приближении).

Для решения задач на расстояние между точками на окружности, необходимо использовать формулу: s = R∠α, где s — длина дуги между точками, α — центральный угол в радианах и R — радиус окружности.

Когда задача связана с вписанными и описанными окружностями, необходимо знать следующие свойства:

• Диаметр, проведенный касательно к окружности, является основанием равнобедренной трапеции;
• Перпендикуляр, проведенный касательно к окружности, проходит через центр этой окружности;
• Вписанный угол равен половине соответствующего центрального угла;
• Описанный угол равен углу, составленному хордой, соединяющей точки пересечения хорды и окружности.

Зная эти свойства, можно подобрать необходимые формулы и решить задачу.

Отработка навыков на тестах и контрольных работах

Чтобы успешно справиться с задачами по геометрии на ОГЭ, необходимо оттачивать свои навыки и умения на тестах и контрольных работах. Следует регулярно заниматься решением различных заданий, выбранных из разных разделов геометрии.

Одной из важных задач на этапе отработки навыков является выборка тестов и контрольных работ по классическим геометрическим конструкциям, которые могут встретиться на ОГЭ:

• Построение перпендикуляра, биссектрисы, медианы и высоты треугольника
• Нахождение площади треугольника
• Нахождение площади четырехугольника
• Нахождение объема тела или площади поверхности призмы

Помимо этого, необходимо уметь работать с теоремами и правилами, связанными с разными геометрическими фигурами (треугольник, круг, прямоугольник, параллелограмм, трапеция и др.). Важно не только знать эти правила, но и уметь их применять при решении задач разной сложности.

Для отработки навыков можно использовать следующие рекомендации:

1. Регулярно решать тесты и контрольные работы с заданиями по геометрии. На начальном этапе это могут быть упражнения на простейшие геометрические конструкции, а затем можно переходить к более сложным заданиям.
2. Анализировать ошибки в процессе решения и находить причины их возникновения. Например, это может быть неправильный выбор теоремы или формулы, ошибка в расчетах, невнимательность при чтении условия задачи.
3. Решать задачи в различных условиях. Например, можно найти решения заданий, используя геометрический чертеж или без него, на рисунке или на «сухую» (без изображения фигуры).

Чем больше практики, тем лучше закрепляются навыки и умения в геометрии. Именно поэтому постоянное решение задач и контрольных работ очень важно на этапе подготовки к ОГЭ по математике.

Актуальные темы геометрии в ОГЭ по математике

Одним из крупных блоков заданий на ОГЭ по математике являются задания по геометрии. Поэтому, важно хорошо подготовиться к этой теме и знать, как решать задачи на геометрию.

Актуальными темами геометрии на ОГЭ являются: построение фигур и применение школьной геометрии. Для решения заданий по геометрии необходимо иметь представление о геометрических фигурах, их свойствах и способах их измерения. Также полезно знать, какими инструментами можно воспользоваться, чтобы построить определенную фигуру.

Важно отметить, что многие задания по геометрии на ОГЭ являются составными и включают в себя несколько этапов. Поэтому, чтобы успешно решать задачи по геометрии, необходимы навыки анализа условия и выделения ключевых моментов, логического мышления и умения распределять время на каждый этап решения задачи.

Необходимо также отметить, что регулярная практика решения задач по геометрии поможет накопить опыт и уверенность в своих знаниях, что будет полезно не только на ОГЭ, но и на ЕГЭ и при поступлении в вуз.

Итак, для успешного прохождения ОГЭ по математике необходимо хорошо подготовиться к заданиям по геометрии, узнать актуальные темы и общие принципы решения задач, приобрести практические навыки и уверенность в своих знаниях.

Стратегии повышения успеваемости по геометрии в ОГЭ по математике

Если вы хотите улучшить свою успеваемость по геометрии в ОГЭ по математике, то следующие стратегии могут вам помочь:

1. Понимание теории. Геометрия требует хорошего понимания теории и определений. Необходимо углублять свои знания в этой области и лучше освоить основные понятия и правила до того, как начать решать задачи.
2. Практика. Чем больше задач вы решите, тем больше у вас будет навыков и опыта. Попробуйте решать разнообразные задачи из разных источников, чтобы научиться применять теорию на практике.
3. Обращение к учителю. Если у вас возникли трудности с какой-то темой, не стесняйтесь обращаться за помощью к учителю. Он всегда готов помочь и объяснить материал более подробно и доступно.
4. Использование графических средств. Графические средства, такие как линейка и угольник, могут очень помочь при решении геометрических задач. Не забывайте использовать их при решении задач.
5. Проверка своих решений. После того, как вы решили задачу, проверьте свое решение. Это поможет увидеть свои ошибки и избежать их в будущем.

Следование этим стратегиям поможет вам улучшить свою успеваемость по геометрии в ОГЭ по математике и достичь более высоких результатов на экзамене.