Прикладная математика в агробиологическом профиле что это

Прикладная математика в агробиологическом профиле – это область науки, которая использует математические методы и моделирование для решения задач, связанных с агробиологическими исследованиями. Эта статья рассказывает о том, как прикладная математика помогает оптимизировать процессы в агробиологии, улучшить урожайность и эффективность сельскохозяйственных культур, а также предсказывать и анализировать различные аспекты развития растений.

Агробиология – это научное направление, которое изучает жизнь растений и животных в агроэкосистемах. Она включает в себя множество дисциплин, в том числе биологию, агрономию, экологию и генетику. Однако одним из ключевых инструментов агробиологии является прикладная математика.

Прикладная математика в агробиологическом профиле помогает решать сложные задачи, связанные с управлением и оптимизацией процессов в сельском хозяйстве. Она позволяет анализировать и моделировать различные агроэкосистемы, предсказывать динамику роста и развития растений, а также оптимизировать использование ресурсов, таких как вода, удобрения и пестициды.

Прикладная математика в агробиологии играет важную роль в разработке эффективных стратегий борьбы с вредителями, оптимизации процессов полива и удобрения, а также прогнозировании урожайности и качества продукции. С помощью математических моделей можно оптимизировать распределение растений на поле, чтобы максимизировать урожайность и снизить затраты на удобрения и воду.

Кроме того, математические методы позволяют проводить анализ данных, полученных в результате экспериментов и наблюдений, и на их основе делать прогнозы о возможных изменениях в агроэкосистемах. Такая информация позволяет агробиологам принимать обоснованные решения и разрабатывать стратегии для повышения устойчивости сельского хозяйства к изменению климата и другим неблагоприятным факторам.

Таким образом, прикладная математика играет ключевую роль в агробиологическом профиле, позволяя решать сложные задачи и улучшать эффективность сельскохозяйственного производства. Она является неотъемлемой частью современной агробиологии и открывает новые возможности для развития устойчивого и инновационного сельского хозяйства.

Прикладная математика и ее значение в агробиологическом профиле

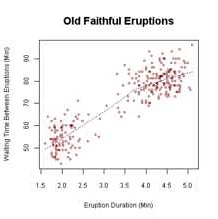
Прикладная математика играет важную роль в агробиологическом профиле, предоставляя инструменты для анализа и решения проблем, связанных с сельским хозяйством и биологией. Она помогает ученым и специалистам разрабатывать и оптимизировать методы и модели, которые позволяют повысить урожайность, улучшить качество продукции и улучшить устойчивость растений к болезням и вредителям.

Одной из основных областей применения прикладной математики в агробиологическом профиле является анализ данных. С помощью статистических методов и моделей можно изучать взаимосвязи между различными факторами и событиями, например, между условиями выращивания растений и их урожайностью. Это позволяет выявлять закономерности и оптимизировать процессы в сельском хозяйстве.

Еще одна область применения прикладной математики в агробиологическом профиле — моделирование. Модели помогают ученым предсказывать результаты различных сценариев и оценивать эффективность различных стратегий. Например, с помощью математических моделей можно определить оптимальные условия выращивания определенной культуры или оптимальное количество удобрений для достижения максимальной урожайности.

Также прикладная математика играет важную роль в генетике и селекции растений. С помощью математических моделей и статистических методов можно анализировать генетические данные и исследовать различные генетические механизмы. Это помогает ученым понять, какие гены отвечают за определенные свойства растений, и разрабатывать новые сорта с улучшенными характеристиками.

Таким образом, прикладная математика является неотъемлемой частью агробиологического профиля, обеспечивая ученым и специалистам необходимые инструменты для анализа данных, моделирования и оптимизации процессов в сельском хозяйстве. Благодаря ей возможно совершенствование методов выращивания растений, разработка новых сортов и повышение эффективности сельскохозяйственного производства.

Видео по теме:

Определение

Прикладная математика в агробиологическом профиле использует такие математические методы, как статистика, оптимизация, моделирование и численные методы, чтобы анализировать данные, оценивать риски, предсказывать результаты и принимать рациональные решения в области агробиологии.

Она находит применение в различных областях агробиологии, включая селекцию растений и животных, генетику, экологию, растениеводство, животноводство, пестициды и удобрения, а также в управлении и планировании сельского хозяйства.

Прикладная математика в агробиологическом профиле играет важную роль в разработке новых методов и подходов к решению сложных проблем, связанных с сельским хозяйством и биологией. Она помогает ученым и практикам принимать обоснованные решения на основе математического анализа и моделирования, что способствует повышению эффективности и устойчивости агробиологических систем.

Основные понятия и принципы прикладной математики

Основными понятиями прикладной математики являются:

Модель	Математическое описание реальной системы или процесса с использованием символов и формул. Модель позволяет анализировать и прогнозировать поведение системы.
Математическое программирование	Метод решения задач оптимизации с использованием математических моделей и алгоритмов. Позволяет находить оптимальные решения при заданных ограничениях.
Статистика	Наука о сборе, анализе, интерпретации и представлении данных. Используется для изучения случайных явлений и принятия решений на основе статистических выводов.
Дифференциальные уравнения	Уравнения, описывающие изменение некоторой величины в зависимости от ее производной. Часто используются для моделирования динамических систем.

Принципы прикладной математики включают:

• Моделирование — создание математических моделей, которые адекватно описывают реальные системы и процессы.
• Анализ — изучение свойств и поведения математических моделей с помощью аналитических и численных методов.
• Оптимизация — нахождение оптимальных решений с использованием математических моделей и алгоритмов оптимизации.
• Статистический анализ — использование статистических методов для анализа и интерпретации данных.

Прикладная математика позволяет решать сложные задачи в агробиологии, такие как оптимизация рационов животных, прогнозирование урожайности и моделирование воздействия пестицидов на экосистемы. Она является мощным инструментом для повышения эффективности и устойчивости сельского хозяйства.

Математические модели

Математические модели позволяют анализировать сложные биологические системы, описывать их динамику и предсказывать результаты изменений внешних условий. Они помогают исследователям и практикам принимать обоснованные решения на основе математических расчетов и экспериментальных данных.

Применение математических моделей в агробиологическом профиле позволяет оптимизировать процессы растениеводства и животноводства, прогнозировать урожайность и рост животных, оценивать влияние различных факторов на их развитие и здоровье.

Для создания математических моделей используются различные методы и подходы, такие как дифференциальные уравнения, статистические модели, оптимизационные методы и другие. Важным этапом в создании моделей является верификация их адекватности – сравнение результатов моделирования с экспериментальными данными и проверка их соответствия.

Математические модели в агробиологическом профиле могут использоваться для решения различных задач, таких как оптимизация распределения удобрений, прогнозирование роста и развития растений и животных, моделирование влияния климатических условий на урожайность и другие.

В итоге, математические модели являются мощным инструментом для анализа и прогнозирования различных аспектов агробиологии. Они помогают улучшить эффективность и устойчивость сельскохозяйственного производства, а также разработать новые методы и технологии для повышения его результативности.

Создание и использование математических моделей в агробиологическом профиле

Математические модели позволяют ученым проводить виртуальные эксперименты, получать предсказания и оценивать эффективность различных сельскохозяйственных практик. Они позволяют прогнозировать и оптимизировать уровень урожайности, управлять использованием ресурсов, определять оптимальные условия для роста и развития растений.

При создании математической модели в агробиологическом профиле необходимо учитывать различные факторы, такие как погодные условия, свойства почвы, наличие вредителей и т. д. Для этого используются различные математические методы и подходы, такие как дифференциальные уравнения, стохастическое моделирование, оптимизация и другие.

Использование математических моделей в агробиологическом профиле позволяет принимать обоснованные решения, основанные на количественных данных и результаты исследований. Они помогают сократить время и затраты на проведение физических экспериментов и оптимизировать процессы в сельском хозяйстве.

Таким образом, создание и использование математических моделей является важным инструментом в агробиологическом профиле, позволяющим эффективно изучать и управлять агробиологическими системами с целью повышения урожайности и улучшения сельскохозяйственных практик.

Статистические методы

Статистические методы оказывают важное влияние на агробиологические исследования, позволяя проводить анализ полученных данных и делать выводы на основе статистических закономерностей.

Одним из наиболее распространенных статистических методов является анализ дисперсии. Этот метод позволяет выявить различия между группами данных и оценить их статистическую значимость. Анализ дисперсии часто применяется для сравнения урожайности разных сортов растений или влияния различных факторов на рост и развитие растений.

Другим важным статистическим методом является корреляционный анализ. Он позволяет определить статистическую связь между двумя или более переменными. Например, корреляционный анализ может быть использован для определения взаимосвязи между уровнем осадков и урожайностью сельскохозяйственных культур.

Статистические методы также позволяют проводить регрессионный анализ, который позволяет оценить зависимость одной переменной от другой. Регрессионный анализ может быть использован для прогнозирования урожайности на основе различных факторов, таких как количество солнечного света, температура и влажность почвы.

Кроме того, статистические методы позволяют проводить анализ временных рядов, сравнивать группы данных с помощью t-теста и проводить множественное сравнение средних значений с помощью анализа дисперсии.

В целом, статистические методы являются неотъемлемой частью агробиологических исследований, позволяя сделать обоснованные выводы на основе полученных данных и повысить эффективность агробиотехнологий и сельскохозяйственного производства.

Применение статистических методов в агробиологии для анализа данных

Статистические методы играют важную роль в анализе данных в агробиологии. Они позволяют исследователям делать выводы о влиянии различных факторов на развитие растений, здоровье животных, качество почвы и другие агробиологические параметры.

Одним из основных статистических методов, применяемых в агробиологии, является анализ вариации. Этот метод позволяет оценить значимость различий между группами, например, между разными сортами растений или различными условиями выращивания. Анализ вариации позволяет оценить вклад каждого фактора в общую вариацию данных и определить, является ли различие статистически значимым.

Другим широко используемым статистическим методом в агробиологии является корреляционный анализ. Этот метод позволяет выявить связь между различными переменными, например, между уровнем удобрений и урожаем или между погодными условиями и ростом растений. Корреляционный анализ помогает исследователям понять, какие факторы влияют на исследуемые агробиологические показатели и насколько сильна эта связь.

Также в агробиологии широко используются дисперсионный анализ, регрессионный анализ, факторный анализ и другие статистические методы. Все они позволяют проводить более точные и надежные исследования, определять важные закономерности и делать обоснованные выводы на основе собранных данных в агробиологических исследованиях.

Оптимизация процессов

Одним из основных применений оптимизации процессов в агробиологии является оптимизация сельскохозяйственного производства. С помощью математических моделей и методов можно определить оптимальное соотношение факторов производства, таких как выбор семенного материала, удобрений, агротехнических приемов и т.д. Это позволяет увеличить урожайность и качество продукции, а также снизить затраты на производство.

Оптимизация процессов также применяется в управлении растениеводством. Математические модели позволяют определить оптимальные условия выращивания растений, такие как температура, освещение, полив и т.д. Это позволяет повысить урожайность и качество продукции, а также снизить риски возникновения болезней и вредителей.

Другим применением оптимизации процессов в агробиологии является оптимизация использования ресурсов. С помощью математических моделей и методов можно определить оптимальное распределение ресурсов, таких как вода, энергия, удобрения и т.д. Это позволяет снизить затраты на производство, а также улучшить экологическую устойчивость агробиологических систем.

В заключение, оптимизация процессов является важным инструментом в агробиологическом профиле. Применение прикладной математики позволяет выбрать оптимальные решения и стратегии, а также повысить эффективность и улучшить результаты работы. Оптимизация процессов в агробиологии способствует увеличению урожайности, улучшению качества продукции и снижению затрат на производство.

Математическое моделирование и оптимизация процессов в агробиологии

Математическое моделирование в агробиологии основано на использовании математических уравнений и статистических методов для описания и анализа процессов, которые происходят в агробиологических системах. Оно позволяет исследовать такие явления, как рост и развитие растений, динамика популяций вредителей, воздействие погодных условий на урожайность и другие важные аспекты агробиологии.

Оптимизация процессов в агробиологии основана на использовании математических моделей для нахождения оптимальных параметров или стратегий воздействия на биологические системы. Например, можно оптимизировать количество удобрений или пестицидов, необходимых для достижения максимальной урожайности при минимальных затратах. Также можно оптимизировать расписание полива или сбора урожая, чтобы получить наилучшие результаты.

Математическое моделирование и оптимизация процессов в агробиологии позволяют принимать обоснованные решения на основе количественных данных и предсказаний, что способствует повышению эффективности и устойчивости сельскохозяйственного производства. Эти методы широко применяются для исследования и улучшения сельскохозяйственных процессов, а также для разработки инновационных методов и технологий в агробиологии.

Вопрос-ответ:

Чем занимается прикладная математика в агробиологическом профиле?

Прикладная математика в агробиологическом профиле занимается разработкой и применением математических методов и моделей для анализа и оптимизации процессов, связанных с сельским хозяйством и биологией. Это включает в себя прогнозирование урожайности, оптимизацию использования ресурсов, моделирование генетических процессов и многое другое.

Какие математические методы используются в агробиологии?

В агробиологии используются различные математические методы, такие как статистика, теория вероятностей, дифференциальные уравнения, оптимизация, моделирование и другие. Эти методы позволяют анализировать данные, прогнозировать результаты экспериментов, оптимизировать параметры процессов и разрабатывать математические модели для описания биологических явлений.

Какую практическую пользу приносит применение прикладной математики в агробиологическом профиле?

Применение прикладной математики в агробиологическом профиле позволяет повысить эффективность и устойчивость сельскохозяйственного производства. С помощью математических методов и моделей можно оптимизировать использование ресурсов, увеличить урожайность, снизить затраты на производство и предсказать результаты экспериментов. Это помогает сельским хозяйственным предприятиям и ученым принимать обоснованные решения и более эффективно управлять процессами.

Какие примеры прикладной математики в агробиологии можно привести?

Примеры прикладной математики в агробиологии включают в себя разработку моделей для прогнозирования урожайности, оптимизацию полива и удобрений, моделирование генетических процессов, анализ данных сельскохозяйственных экспериментов, прогнозирование распространения вредителей и болезней, а также многое другое. Эти методы и модели помогают сельскому хозяйству стать эффективнее, устойчивее и экологически безопаснее.

Какая роль математики в агробиологическом профиле?

Математика играет важную роль в агробиологическом профиле. Она помогает анализировать и моделировать различные процессы, связанные с ростом и развитием растений, оптимизировать использование ресурсов, прогнозировать урожайность, а также планировать и оптимизировать эксперименты. Без математического подхода в агробиологии было бы сложно понять и объяснить многие явления, происходящие в растительном мире.

Какие методы математики применяются в агробиологическом профиле?

В агробиологическом профиле применяются различные методы математики, такие как статистика, математическое моделирование, оптимизация, анализ данных и т.д. Статистика позволяет анализировать и интерпретировать полученные данные, выявлять закономерности и делать выводы. Математическое моделирование помогает создавать математические модели, которые описывают различные процессы роста и развития растений, а также прогнозировать их поведение в различных условиях. Оптимизация позволяет находить оптимальные решения для различных задач, например, оптимальное распределение ресурсов или оптимальное время посева. Анализ данных позволяет обрабатывать и интерпретировать полученную информацию, выявлять тенденции и закономерности, а также делать прогнозы и принимать решения на основе этих данных.