Что такое произведения чисел в математике 4 класс

Произведение чисел в математике 4 класса — это результат умножения двух или более чисел. Узнайте, как находить произведение чисел и применять его в решении задач в 4 классе.

Одной из основных операций в математике является умножение, которое позволяет находить произведение двух или более чисел. Произведение чисел — это результат умножения. В четвертом классе ученики изучают основные понятия и правила умножения, а также применяют их на практике.

Одно из ключевых понятий, которое изучают в четвертом классе, — это таблица умножения. Таблица умножения представляет собой специальную таблицу, в которой перечислены все произведения чисел от 1 до 10. Она помогает детям запомнить основные результаты умножения и использовать их в решении различных задач.

Например, чтобы найти произведение двух чисел, нужно найти значение пересечения строки и столбца, в которых находятся данные числа в таблице умножения. Например, если нужно найти произведение 3 и 4, то нужно найти пересечение третьей строки и четвертого столбца. В результате получается число 12, которое является произведением 3 и 4.

В четвертом классе также изучают основные свойства умножения, такие как коммутативность и ассоциативность. Коммутативное свойство гласит, что порядок множителей не влияет на результат умножения. Например, произведение 2 и 3 равно произведению 3 и 2. Ассоциативное свойство умножения гласит, что порядок скобок при умножении не влияет на результат. Например, произведение (2 * 3) * 4 равно произведению 2 * (3 * 4).

Что такое произведение чисел?

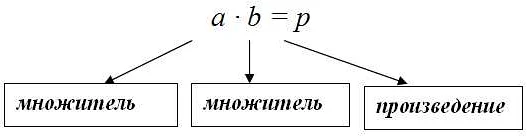
В произведении чисел каждое из них называется множителем. Множители могут быть любыми числами: целыми, дробными или отрицательными. Произведение двух одинаковых чисел называется квадратом этого числа. Например, произведение числа 5 на само себя будет 5×5=25 или 5⋅5=25, и это будет квадрат числа 5.

Произведение чисел имеет ряд свойств. Например, свойства коммутативности и ассоциативности. Свойство коммутативности означает, что результат умножения двух чисел не зависит от порядка этих чисел. Например, 2×3=6 и 3×2=6. Свойство ассоциативности означает, что результат умножения трех или более чисел не зависит от того, в каком порядке производить умножение. Например, (2×3)×4=24 и 2×(3×4)=24.

Произведение чисел играет важную роль в математике и имеет множество применений в реальной жизни. Например, оно используется для нахождения площади прямоугольника или квадрата, для определения количества предметов в группе, для вычисления стоимости товаров и многое другое.

Определение и основные понятия

Основные понятия, связанные с произведением чисел:

1. Множители – числа, которые участвуют в произведении. В умножении 3×4, числа 3 и 4 являются множителями.
2. Произведение – результат умножения множителей. В умножении 3×4, произведением будет число 12.
3. Умножение – операция, при которой происходит сложение одного числа с собой несколько раз.

Произведение чисел можно рассматривать как повторение одного и того же числа несколько раз. Например, произведение числа 5 на 3 (5×3) можно представить как сумму пяти пятерок (5+5+5), что равно 15.

Умножение чисел имеет свои особенности, такие как коммутативность и ассоциативность. Коммутативность означает, что порядок умножения множителей не влияет на результат, например, 3×4=4×3. Ассоциативность означает, что результат умножения не зависит от расстановки скобок при умножении трех и более чисел, например, (2×3)×4=2×(3×4).

Умножение является одной из основных арифметических операций и широко применяется в различных областях науки и повседневной жизни.

Как найти произведение чисел?

Произведение двух чисел можно найти, умножив их друг на друга. Например, чтобы найти произведение чисел 4 и 5, нужно умножить 4 на 5 и получить результат 20. В математике произведение обозначается знаком умножения «x» или точкой «·».

Для нахождения произведения нескольких чисел нужно умножить все эти числа между собой. Например, чтобы найти произведение чисел 2, 3 и 4, нужно умножить 2 на 3, а затем полученный результат умножить на 4, итоговое произведение будет равно 24.

При умножении чисел важно помнить, что порядок умножения не влияет на результат. Например, произведение чисел 2 и 3 будет равно произведению чисел 3 и 2, то есть 6.

В математике также существуют особые случаи произведения чисел. Произведение числа на 0 всегда будет равно 0. Например, произведение числа 7 на 0 будет равно 0. Также произведение любого числа на 1 будет равно этому числу. Например, произведение числа 9 на 1 будет равно 9.

Нахождение произведения чисел является одной из основных операций в математике. Умение правильно находить произведение чисел помогает в решении различных задач и проблем, а также является основой для более сложных математических операций.

Примеры произведения чисел

Например, произведение чисел 3 и 4 равно 12, так как 3 умножить на 4 равно 12.

Другой пример: произведение чисел 5 и 2 равно 10, так как 5 умножить на 2 равно 10.

Произведение числа на единицу всегда равно этому числу. Например, произведение числа 7 на 1 равно 7.

Таблица ниже показывает еще несколько примеров произведений чисел:

Первое числоВторое числоПроизведение

2	3	6
4	5	20
6	2	12

В этих примерах, мы умножаем первое число на второе число и получаем произведение.

Свойства произведения чисел

Свойство коммутативности умножения гласит, что порядок сомножителей не влияет на результат произведения. Например, произведение чисел 3 и 4 равно 12, и это же произведение можно получить, поменяв местами сомножители: произведение чисел 4 и 3 также равно 12.

Свойство ассоциативности умножения гласит, что порядок скобок при умножении трех или более чисел не влияет на результат. Например, произведение чисел 2, 3 и 4 можно вычислить двумя способами: (2 * 3) * 4 = 6 * 4 = 24 или 2 * (3 * 4) = 2 * 12 = 24. В обоих случаях результат будет равен 24.

Свойство нулевого элемента умножения гласит, что произведение числа на ноль всегда равно нулю. Например, любое число, умноженное на ноль, будет равно нулю: 2 * 0 = 0 и 5 * 0 = 0.

Свойство единичного элемента умножения гласит, что произведение числа на единицу всегда равно этому числу. Например, любое число, умноженное на единицу, будет равно самому себе: 3 * 1 = 3 и 7 * 1 = 7.

Знание этих свойств поможет упростить вычисления и понять особенности произведения чисел.

Произведение чисел в математике 4 класс: примеры задач

Рассмотрим несколько примеров задач, в которых требуется найти произведение чисел:

Пример 1: Найдите произведение чисел 5 и 2.

Решение: Чтобы найти произведение чисел, нужно умножить эти числа. В данном случае, 5 × 2 = 10. Таким образом, произведение чисел 5 и 2 равно 10.

Пример 2: Найдите произведение чисел 7 и 3.

Решение: Для нахождения произведения чисел 7 и 3, нужно перемножить эти числа. 7 × 3 = 21. Таким образом, произведение чисел 7 и 3 равно 21.

Пример 3: Найдите произведение чисел 4, 5 и 2.

Решение: Чтобы найти произведение трех чисел, нужно перемножить все эти числа. В данном случае, 4 × 5 × 2 = 40. Таким образом, произведение чисел 4, 5 и 2 равно 40.

Произведение чисел может быть использовано для решения различных задач и вычислений в математике. Знание этого понятия позволяет ученикам легче справляться с задачами и улучшает их навыки в умножении.

Вопрос-ответ:

Что такое произведение двух чисел?

Произведение двух чисел — это результат умножения этих чисел. Например, произведение чисел 5 и 3 равно 15.

Как записать произведение чисел?

Произведение чисел можно записать в виде умножения. Например, произведение чисел 2 и 4 можно записать как 2 * 4.

Как найти произведение чисел с помощью таблицы умножения?

Для нахождения произведения чисел с помощью таблицы умножения нужно найти в ней число, соответствующее первому множителю, а затем в этом столбце найти число, соответствующее второму множителю. Найденное число и будет произведением данных чисел.

Как найти произведение чисел, если одно из них ноль?

Если одно из чисел, которые нужно умножить, равно нулю, то произведение всегда будет равно нулю. Например, произведение чисел 0 и 6 равно 0.

Можно ли найти произведение чисел с помощью сложения?

Да, произведение чисел можно найти с помощью сложения. Например, произведение чисел 3 и 4 можно найти, сложив число 4 три раза: 4 + 4 + 4 = 12.

Практическое применение произведения чисел

Одним из примеров практического применения произведения чисел является вычисление площади прямоугольника или квадрата. Площадь прямоугольника можно вычислить, умножив длину одной из сторон на длину другой стороны. Например, если длина прямоугольника равна 5 см, а ширина – 3 см, то площадь будет равна 5 * 3 = 15 см².

Другим примером применения произведения чисел является умножение количества предметов на их стоимость. Например, если у вас есть 2 яблока, стоимость которого составляет 10 рублей за штуку, то общая стоимость яблок будет равна 2 * 10 = 20 рублей.

Также произведение чисел может использоваться для вычисления времени или расстояния. Например, если вы двигаетесь со скоростью 40 км/час в течение 3 часов, то расстояние, которое вы пройдёте, можно вычислить, умножив скорость на время: 40 * 3 = 120 км.

В общем случае, произведение чисел может быть полезным инструментом для решения различных задач в повседневной жизни, инженерии, экономике и других областях.

Примеры практического применения произведения чисел:

Вычисление площади прямоугольника или квадрата

Умножение количества предметов на их стоимость

Вычисление времени и расстояния

Решение задач в различных областях

Видео по теме: