Произведения это в математике что это

Произведение является одной из основных операций в математике. Оно позволяет умножать числа, выражения, функции и многое другое. Узнайте, как работает произведение и как его применять в различных математических задачах.

Произведения являются одним из важнейших понятий в математике. Они используются для умножения чисел, но их значение и применение выходят далеко за рамки элементарной арифметики.

Произведение двух чисел представляет собой результат их умножения. Например, произведение чисел 3 и 4 равно 12. Но произведения также могут быть выражены в виде символов и переменных, что позволяет использовать их для решения более сложных математических задач.

Произведения широко применяются в различных областях математики, включая алгебру, геометрию, анализ, теорию вероятностей и дискретную математику. Они позволяют описывать и анализировать связи и взаимодействия между числами, объектами и явлениями.

Произведения также играют ключевую роль в формулировке и доказательстве математических теорем. Они позволяют установить закономерности, выявить общие свойства чисел и объектов, а также разработать эффективные методы и алгоритмы для решения задач.

Особое значение произведений имеет векторное произведение, которое используется в линейной алгебре, физике, геометрии и других науках. Оно позволяет определить ортогональность, параллельность и другие важные характеристики векторов и плоскостей.

Что такое произведения в математике?

Произведение также может быть представлено в виде таблицы умножения, где каждое число из первого множества умножается на каждое число из второго множества. Например, таблица умножения для чисел от 1 до 5 будет содержать все возможные произведения пар чисел от 1 до 5.

Произведение имеет несколько важных свойств. Одно из них — коммутативность. Это значит, что порядок, в котором умножаются числа, не влияет на результат. Например, произведение чисел 2 и 3 равно 6, и произведение чисел 3 и 2 также равно 6.

Другое важное свойство — ассоциативность. Это означает, что при умножении трех или более чисел результат не зависит от порядка, в котором они умножаются. Например, произведение чисел 2, 3 и 4 будет одинаковым, независимо от того, сначала умножим 2 на 3, а затем полученное произведение на 4, или сначала умножим 3 на 4, а затем полученное произведение на 2.

Произведения в математике широко используются для решения различных задач и применяются во многих областях, таких как физика, экономика и программирование. Они помогают представить взаимосвязь между различными величинами и найти значения неизвестных величин.

Определение и основные понятия

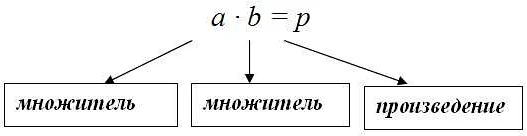
Главное понятие, связанное с произведением, — это множители. Множители — это числа, которые участвуют в операции произведения и влияют на ее результат.

Произведение двух чисел обозначается знаком «×» или «*», и записывается в виде a × b или a * b, где a и b — множители.

Основные свойства произведения:

• Коммутативность: a × b = b × a
• Ассоциативность: (a × b) × c = a × (b × c)
• Дистрибутивность: a × (b + c) = (a × b) + (a × c)

Произведение также имеет нейтральный элемент, который называется единицей. Умножение на единицу не изменяет значение числа.

Произведения широко используются в различных областях математики, таких как алгебра, геометрия, теория вероятностей и других. Они позволяют решать задачи, моделировать явления и выражать зависимости между величинами.

Значение произведений в математике

Произведения в математике играют важную роль и имеют различные значения. Они позволяют умножать числа, объединять группы объектов и выражать повторяющиеся операции.

В основе произведений лежит операция умножения, которая позволяет увеличивать значение числа в определенное количество раз. Например, произведение 5 * 3 означает умножение числа 5 на число 3 и дает результат 15. Это основное значение произведений в математике — получение нового числа путем повторения операции умножения.

Однако произведения могут иметь и другие значения. Например, они могут использоваться для объединения групп объектов. Например, если у нас есть 3 корзины, в каждой из которых лежит по 4 яблока, то общее количество яблок можно выразить как произведение 3 * 4 = 12. Таким образом, произведения могут помочь нам объединить группы и определить общее количество объектов.

Также произведения могут использоваться для выражения повторяющихся операций. Например, если мы хотим посчитать сумму чисел от 1 до 10, то можем использовать произведение 10 * (10 + 1) / 2, где 10 — это количество чисел, а (10 + 1) / 2 — среднее значение суммы первого и последнего числа. Таким образом, произведение позволяет нам выразить сложные вычисления и упростить задачу.

Таким образом, произведения в математике имеют различные значения и позволяют нам умножать числа, объединять группы объектов и выражать повторяющиеся операции. Они являются важным инструментом для решения различных задач и исследования математических закономерностей.

Роль произведений в решении задач

Произведения играют важную роль в математике и часто используются для решения задач различных типов. Они позволяют нам учитывать взаимосвязь между различными величинами и выражать ее с помощью одного числа.

Первая и самая простая роль произведений заключается в умножении чисел. Умножение позволяет нам находить произведение двух или более чисел и получать результат, который является их общей мерой или количественным выражением их взаимосвязи.

Кроме того, произведения используются для нахождения площади прямоугольника или квадрата. Площадь — это произведение длины и ширины фигуры, и она позволяет нам измерять площадь поверхности или площадь ограниченной области.

Для решения задач на пропорциональное деление или распределение произведения используется для нахождения отношения между различными частями целого. Например, если мы имеем две части, и одна часть составляет 3/4 от всего, то мы можем выразить это отношение с помощью произведения: (3/4) * целое.

В произведениях также используются для вычисления вероятности событий. Вероятность — это отношение числа благоприятных исходов к общему числу исходов, и произведение позволяет нам вычислить эту вероятность.

Таким образом, произведения играют важную роль в решении задач различных типов и позволяют нам выражать взаимосвязь между различными величинами с помощью одного числа.

Примеры применения произведений

Произведения в математике имеют широкий спектр применений и используются для решения различных задач. Вот несколько примеров их применения:

1. Умножение чисел: Произведение двух чисел показывает, насколько большое будет итоговое значение, когда одно число умножается на другое. Это основное применение произведений в арифметике.

2. Вычисление площади: В геометрии произведения используются для вычисления площади различных фигур. Например, площадь прямоугольника равна произведению его длины и ширины.

3. Решение уравнений: Произведения часто используются при решении уравнений и систем уравнений. Они позволяют выразить связь между различными переменными и найти значения, удовлетворяющие уравнению.

4. Вероятность: В теории вероятности произведения используются для вычисления вероятности совместного наступления нескольких событий. Например, вероятность выпадения двух определенных чисел на игральной кости равна произведению их вероятностей.

5. Производная: В математическом анализе произведения используются для вычисления производной функции. Например, производная произведения двух функций равна произведению производной каждой из них.

Это только некоторые примеры применения произведений в математике. Они являются важным инструментом при решении различных задач и находят применение во многих областях науки и техники.

Произведения в различных областях математики

В арифметике произведение часто используется для определения общего количества элементов в нескольких группах. Например, если у нас есть 3 коробки, каждая из которых содержит по 4 яблока, мы можем узнать общее количество яблок, умножив число коробок на число яблок в каждой коробке (3 * 4 = 12).

В алгебре произведение часто используется для выражения зависимости между двумя или более переменными. Например, если у нас есть две переменные x и y, мы можем записать их произведение как xy. Это позволяет нам описывать и анализировать различные математические отношения и модели.

В теории вероятности произведение часто используется для вычисления вероятности двух или более независимых событий. Например, если вероятность события A равна 0.5, а вероятность события B равна 0.3, вероятность того, что оба события произойдут, будет равна произведению их вероятностей (0.5 * 0.3 = 0.15).

В теории чисел произведение часто используется для анализа свойств простых чисел и их разложения на множители. Например, можно разложить число 12 на простые множители 2, 2 и 3, и записать его как 2 * 2 * 3. Это позволяет нам лучше понять структуру чисел и решать различные задачи.

Произведения также имеют важное значение в других областях математики, таких как геометрия, математическая логика и математическая физика. Они предоставляют нам универсальный инструмент для работы с числами, объектами и идеями, и позволяют нам строить сложные модели и решать различные задачи.

Произведения и их свойства

Произведения имеют свои особенности и свойства, которые позволяют более эффективно работать с ними. Некоторые из них:

Коммутативность: Произведение двух чисел не зависит от порядка, в котором они умножаются. Другими словами, для любых чисел a и b выполняется равенство a * b = b * a.

Ассоциативность: Произведение трех или более чисел не зависит от порядка, в котором они умножаются. Другими словами, для любых чисел a, b и c выполняется равенство (a * b) * c = a * (b * c).

Дистрибутивность: Произведение числа a на сумму чисел b и c равно сумме произведений a на b и a на c. Другими словами, для любых чисел a, b и c выполняется равенство a * (b + c) = (a * b) + (a * c).

Единичный элемент: Умножение числа на 1 не меняет его значения. Другими словами, для любого числа a выполняется равенство a * 1 = a.

Ноль: Умножение числа на 0 дает 0. Другими словами, для любого числа a выполняется равенство a * 0 = 0.

Произведения и их свойства широко применяются в различных областях математики, физики, экономики и других науках. Они являются важным инструментом для решения задач и проведения исследований.

Вопрос-ответ:

Какие произведения существуют в математике?

В математике существует множество видов произведений, включая числовое произведение, векторное произведение, матричное произведение и т. д.

Зачем нужны произведения в математике?

Произведения в математике используются для решения различных задач и моделирования реальных явлений. Они позволяют умножать числа, комбинировать векторы, перемножать матрицы и многое другое.

Какими свойствами обладают произведения в математике?

Произведения в математике обладают рядом свойств, таких как ассоциативность (порядок умножения не влияет на результат), коммутативность (умножение можно менять местами), дистрибутивность (умножение распространяется на сложение), идемпотентность (умножение числа на себя даёт тот же результат) и многие другие.

Как применяются произведения в физике и инженерии?

В физике и инженерии произведения используются для моделирования и анализа различных явлений. Например, векторное произведение используется для определения момента силы, матричное произведение — для преобразования координат и решения систем линейных уравнений, числовое произведение — для вычисления работы и многого другого.

Какие примеры произведений можно привести из повседневной жизни?

Произведения можно встретить в различных ситуациях повседневной жизни. Например, при покупке продуктов в магазине мы считаем сумму произведения количества товаров на их цену. Также, произведения используются при расчете площади фигур, объема жидкостей и многих других вещей.

Какие произведения существуют в математике?

В математике существует множество различных произведений, таких как произведение чисел, произведение множеств, произведение матриц и т.д.

Произведения в теории вероятностей и статистике

В теории вероятностей произведение вероятностей двух или более событий используется для определения вероятности исхода, который происходит при наступлении всех этих событий одновременно. Например, если вероятность того, что событие А произойдет, равна 0.8, а вероятность того, что событие В произойдет, равна 0.6, то вероятность того, что и событие А, и событие В произойдут одновременно, равна 0.8 * 0.6 = 0.48.

В статистике произведения используются, например, для определения совместной плотности вероятности или среднего значения случайных величин, которые зависят друг от друга. Например, при рассмотрении зависимости двух случайных величин X и Y, произведение плотностей вероятности f(x) и g(y) позволяет определить совместную плотность вероятности f(x, y). Аналогично, произведение математических ожиданий E(X) и E(Y) позволяет определить среднее значение совместной случайной величины E(XY).

Произведения в теории вероятностей и статистике являются важным инструментом для анализа случайных явлений, моделирования и принятия решений на основе данных. Они позволяют учитывать зависимости между событиями или случайными величинами и предсказывать их поведение в сложных ситуациях.

Видео по теме: