Что такое распределительное свойство в математике 6 класс

Распределительное свойство в математике 6 класс – это одно из основных правил, которое позволяет упростить вычисления с использованием операций сложения и умножения. Ученики 6 класса узнают, как применять распределительное свойство для упрощения математических выражений и решения уравнений. В этой статье рассмотрены примеры и объяснения распределительного свойства в математике 6 класса.

Распределительное свойство – одно из основных понятий в математике, которое активно изучается в 6 классе. Это свойство операций сложения и умножения, которое позволяет производить вычисления с числами в произвольной последовательности. Понимание распределительного свойства является важным элементом формирования математической грамотности у учащихся.

Распределительное свойство гласит, что при выполнении операции умножения числа на сумму двух других чисел, результат будет равен сумме произведений каждого из этих чисел на данное число. Другими словами, умножение распределяется на сложение. Это свойство позволяет упростить вычисления и решение задач, а также существенно ускоряет процесс работы с числами.

Пример:

Дано выражение 2 * (3 + 4).

Согласно распределительному свойству, мы можем сначала выполнить операцию в скобках: 3 + 4 = 7. Затем умножаем 2 на результат: 2 * 7 = 14.

Таким образом, значение выражения 2 * (3 + 4) равно 14.

Распределительное свойство широко используется в различных областях математики, а также в решении задач из реального мира. Понимание и умение применять это свойство поможет учащимся успешно решать задачи на уровне 6 класса, а также будет полезным в дальнейшем изучении математики.

Распределительное свойство в математике 6 класс

Распределительное свойство гласит: при сложении (или вычитании) нескольких чисел с одним числом можно выполнить операцию с каждым из них по отдельности, а затем сложить (или вычесть) полученные результаты.

Например, пусть дано выражение 3 * (2 + 4). Согласно распределительному свойству, мы можем сначала выполнить операцию в скобках, получив 3 * 6, а затем умножить полученный результат на 3, что даст итоговый ответ 18.

Также распределительное свойство применяется и при работе со сложением. Например, если у нас есть выражение 2 * (3 + 5), то мы можем сначала выполнить операцию в скобках, получив 2 * 8, а затем умножить полученный результат на 2, что даст итоговый ответ 16.

Распределительное свойство позволяет существенно упростить вычисления и делает их более удобными. Оно широко применяется в математике и других науках, где требуется работа с арифметическими операциями.

Основные понятия

Например, для сложения чисел выполняется следующее распределительное свойство: если даны числа a, b и c, то сумма a + (b + c) будет равна (a + b) + c. То есть, порядок чисел в сумме не влияет на ее результат.

Аналогично, для умножения чисел выполняется распределительное свойство: если даны числа a, b и c, то произведение a * (b * c) будет равно (a * b) * c. То есть, порядок чисел в произведении не влияет на его результат.

Распределительное свойство является одним из основных понятий в математике и активно используется при работе с числовыми выражениями и алгебраическими формулами.

Примеры распределительного свойства

Умножение числа на сумму двух чисел:

Для любых чисел a, b и c выполняется следующее равенство:

a(b + c) = a·b + a·c

Например, для чисел a = 2, b = 3 и c = 4, мы можем записать:

2(3 + 4) = 2·3 + 2·4

Это можно упростить до:

2·7 = 6 + 8

Таким образом, мы получаем:

14 = 14

Что доказывает, что распределительное свойство выполняется.

Распределительное свойство с вычитанием:

Распределительное свойство также распространяется на операцию вычитания. Для любых чисел a, b и c выполняется следующее равенство:

a(b — c) = a·b — a·c

Например, для чисел a = 5, b = 8 и c = 2, мы можем записать:

5(8 — 2) = 5·8 — 5·2

Это можно упростить до:

5·6 = 40 — 10

Таким образом, мы получаем:

30 = 30

Что также доказывает, что распределительное свойство выполняется.

Распределительное свойство позволяет упростить выражения и легче выполнять операции с числами. Оно является важным инструментом в алгебре и применяется во многих математических задачах.

Понятие операций

Основными операциями в математике являются сложение, вычитание, умножение и деление. Они обладают свойствами, которые позволяют их комбинировать и выполнять в определенном порядке. Одно из таких свойств — распределительное свойство.

Распределительное свойство гласит, что умножение числа на сумму двух чисел равно сумме произведений этого числа на каждое из этих чисел по отдельности.

Распределительное свойство:

a * (b + c) = a * b + a * c

Например, если у нас есть выражение 2 * (3 + 4), то по распределительному свойству мы можем сначала выполнить операцию в скобках: 2 * 7. Затем полученный результат 14 мы можем умножить на 2: 14 * 2. Итоговый результат равен 28.

Распределительное свойство позволяет упростить выражения и выполнить операции в определенном порядке, что является важным понятием в математике.

Сложение и умножение чисел

Например, при сложении чисел 3 и 4 получается сумма 7: 3 + 4 = 7. Здесь 3 и 4 называются слагаемыми, а 7 — суммой.

При умножении числа на другое число, оно повторяется столько раз, сколько указано во втором числе. Например, при умножении числа 5 на 3 получается произведение 15: 5 × 3 = 15. Здесь 5 называется множителем, 3 — множителем, а 15 — произведением.

Сложение и умножение чисел обладают рядом важных свойств, включая коммутативность, ассоциативность и распределительное свойство. Знание этих свойств поможет вам легче решать задачи и делать математические операции.

Использование распределительного свойства

Распределительное свойство гласит, что умножение или деление числа на сумму (или разность) двух других чисел эквивалентно умножению (или делению) этого числа на каждое из двух других чисел, а затем сложению (или вычитанию) полученных произведений.

Например, для выражения (3 + 4) * 5, мы можем использовать распределительное свойство и умножить каждое из чисел в скобках на 5, а затем сложить полученные произведения: 3 * 5 + 4 * 5 = 15 + 20 = 35.

Также распределительное свойство может быть использовано при делении. Например, для выражения (10 + 6) / 2, мы можем использовать распределительное свойство и разделить каждое из чисел в скобках на 2, а затем сложить полученные частные: 10 / 2 + 6 / 2 = 5 + 3 = 8.

Использование распределительного свойства позволяет значительно упростить сложные выражения и сделать их более понятными и удобными для вычислений. Это одно из основных инструментов в алгебре, которое помогает решать различные задачи и применять математические операции.

Примеры с распределительным свойством

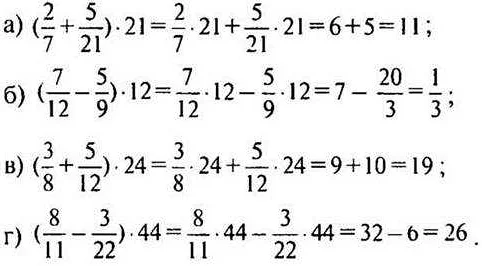
Рассмотрим несколько примеров с применением распределительного свойства:

1. 1. Упростим выражение: 2 * (3 + 4).

Сначала выполним операцию внутри скобок: 3 + 4 = 7.

Затем умножим полученную сумму на 2: 2 * 7 = 14.

Таким образом, выражение 2 * (3 + 4) равно 14.

1. 1. Преобразуем выражение: (5 — 2) * (4 + 3).

Выполним операции внутри скобок: 5 — 2 = 3 и 4 + 3 = 7.

Затем умножим полученные значения: 3 * 7 = 21.

Итак, выражение (5 — 2) * (4 + 3) равно 21.

1. 1. Раскроем скобки в выражении: 3 * (2 — 5) + 4 * (3 — 1).

Операции внутри первой скобки: 2 — 5 = -3.

Операции внутри второй скобки: 3 — 1 = 2.

Умножим первое значение на 3: 3 * (-3) = -9.

Умножим второе значение на 4: 4 * 2 = 8.

Сложим полученные произведения: -9 + 8 = -1.

Таким образом, выражение 3 * (2 — 5) + 4 * (3 — 1) равно -1.

Приведенные примеры демонстрируют применение распределительного свойства при выполнении операций с числами. Это позволяет упростить выражения и получить более компактный и понятный результат.

Выводы о распределительном свойстве

Основные выводы о распределительном свойстве:

1. Распределительное свойство гласит, что при выполнении операции над числами, результат не изменяется, если соединить два числа с помощью данной операции, а затем выполнить ту же операцию над полученным результатом.
2. Это свойство выполняется для операций сложения и умножения.
3. Распределительное свойство можно использовать для упрощения выражений и выполнения операций.
4. Например, при умножении числа на сумму двух чисел, можно сначала выполнить умножение каждого числа на данное число, а затем сложить полученные результаты.
5. Также, при сложении двух сумм чисел, можно сначала сложить числа внутри каждой суммы, а затем сложить полученные результаты.

Распределительное свойство является важным инструментом в алгебре и помогает упростить вычисления и решение уравнений.

Видео по теме:

Что такое распределительное свойство в математике?

Распределительное свойство в математике — это особое свойство операций сложения и умножения, которое позволяет переставлять и складывать или умножать числа в любом порядке.

Как можно применить распределительное свойство в математике?

Распределительное свойство можно применять для упрощения арифметических операций. Например, при сложении или умножении числа на скобку можно распределить операцию на каждый член скобки.

Как распределительное свойство помогает в решении математических задач?

Распределительное свойство позволяет упростить сложные выражения и сократить количество операций. Это помогает решать задачи более эффективно и быстро.