Что такое разность в математике 1 класс в примерах

Разность в математике 1 класса — это операция вычитания, которая позволяет найти разницу между двумя числами. В данной статье представлены примеры разных задач, где требуется найти разность, чтобы помочь ученикам лучше понять эту математическую операцию.

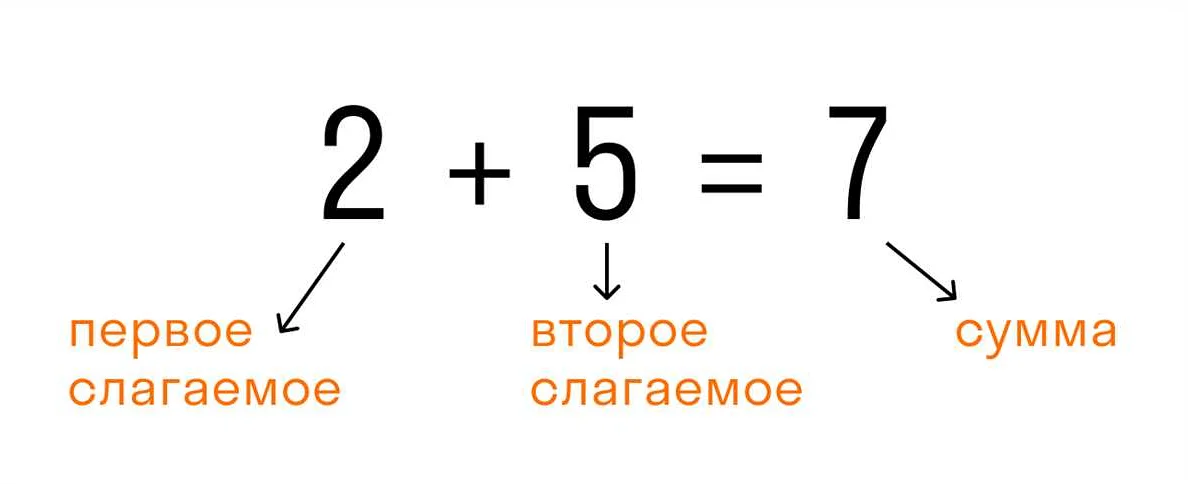
Разность — одно из основных понятий в математике, которое изучается уже в первом классе. Разность — это результат вычитания одного числа из другого. Изучение разности помогает детям понять основы математических операций и развить навыки решения простых задач.

В первом классе, дети начинают изучать простые примеры вычитания, чтобы научиться находить разность двух чисел. Например, если у нас есть 5 яблок и мы съедаем 2, то разность будет равна 3. Это можно записать как 5 — 2 = 3. Такие примеры помогают детям понять, что разность — это то, сколько осталось после вычитания.

Помимо простых примеров, дети также учатся работать с большими числами и находить разность между ними. Например, если у нас есть число 10 и мы вычитаем из него число 7, то разность будет равна 3. Такие задачи помогают детям развить навыки вычитания и понять, как можно вычитать числа даже в случае, когда одно число больше другого.

Изучение разности в математике 1 класса является важным шагом в математическом развитии ребенка. Это позволяет им научиться работать с числами, развить логическое мышление и решать простые задачи. Понимание понятия разности помогает детям развить навыки работы с числами и подготавливает их к изучению более сложных математических операций в будущем.

Что такое разность в математике?

Например, если у нас есть два числа: 5 и 3, то разность между ними будет 2 (5 — 3 = 2). В данном случае, число 5 является уменьшаемым, а число 3 — вычитаемым. Разность показывает, сколько больше или меньше уменьшаемое число относительно вычитаемого.

Также разность может быть вычислена для более сложных выражений, содержащих переменные или другие операции. В этом случае, мы используем те же самые правила для вычитания чисел, но применяем их к каждому члену выражения по отдельности.

Например, если у нас есть выражение 2x — 3y, то разность между этими двумя членами будет представлена как (2x) — (3y). Мы вычитаем одно выражение из другого, применяя правила вычитания к каждому члену отдельно.

Таким образом, разность в математике позволяет нам определить, насколько больше или меньше одно число или выражение относительно другого. Она является важной операцией и используется в различных областях математики и повседневной жизни.

Понятие разности

В математике понятие разности относится к операции вычитания. Разность двух чисел можно найти, вычитая из большего числа меньшее число. Например, разность чисел 9 и 4 равна 5, так как 9 минус 4 равно 5.

Разность можно представить с помощью вычитания:

9 — 4 = 5

Разность чисел также можно представить на числовой прямой. Например, если на числовой прямой отметить число 9 и от него отложить 4 единицы влево, то получится число 5.

Разность может быть как положительной, так и отрицательной. Например, разность чисел 4 и 9 равна -5, так как 4 минус 9 равно -5.

Разность чисел можно находить не только с помощью вычитания, но и с помощью других операций. Например, разность чисел 9 и 4 можно также найти, сложив число 4 с некоторым числом, чтобы получить 9. В этом случае разность будет равна 5, так как 9 минус 4 равно 5.

Понимание понятия разности является важным для решения математических задач, а также для дальнейшего изучения арифметики и алгебры.

Примеры разности в математике

Пример 1:

У нас есть 5 яблок, и мы съедаем 2 из них. Какое количество яблок останется?

Для решения этой задачи мы можем вычесть количество съеденных яблок из общего количества:

5 — 2 = 3

Таким образом, останется 3 яблока.

Пример 2:

Есть 10 книг на полке, а мы взяли 4 книги. Сколько книг останется на полке?

Мы можем использовать вычитание, чтобы найти количество книг, оставшихся на полке:

10 — 4 = 6

На полке останется 6 книг.

Пример 3:

У нас есть 8 конфет, а мы отдали 3 конфеты другу. Сколько конфет у нас осталось?

Вычитаем количество отданных конфет из общего количества:

8 — 3 = 5

У нас осталось 5 конфет.

Пример 4:

На столе лежат 15 шариков, а мы забрали 7 шариков. Сколько шариков осталось на столе?

Вычитаем количество забранных шариков:

15 — 7 = 8

На столе осталось 8 шариков.

Пример 5:

У нас есть 20 рублей, а мы потратили 12 рублей. Сколько денег у нас осталось?

Вычитаем потраченные деньги из общей суммы:

20 — 12 = 8

У нас осталось 8 рублей.

Как вычислять разность

В математике, разность двух чисел можно вычислить, вычитая одно число из другого. Разность показывает, насколько одно число отличается от другого.

Для вычисления разности, необходимо взять число, от которого нужно отнять (уменьшаемое), и число, которое нужно вычесть (вычитаемое). Затем, вычитаемое число вычитается из уменьшаемого числа, что дает нам разность.

Например, если у нас есть выражение «5 — 3», то уменьшаемое равно 5, а вычитаемое равно 3. Вычитаем 3 из 5, получим разность равную 2.

Также, можно представить разность как сравнение двух чисел на числовой оси. Если одно число находится слева от другого, то разность будет положительной. Если одно число находится справа от другого, то разность будет отрицательной.

Например, если у нас есть выражение «3 — 5», то уменьшаемое равно 3, а вычитаемое равно 5. Так как 3 находится слева от 5 на числовой оси, то разность будет отрицательной и равной -2.

Практическое применение разности

В бухгалтерии и финансовой сфере разность используется для вычисления разницы между доходами и расходами. Например, если у вас был доход в размере 1000 рублей, а расходы составили 500 рублей, то разность между ними будет равна 500 рублей. Это позволяет оценить финансовое положение и определить прибыль или убыток.

В торговле и экономике разность используется для вычисления изменения цен. Например, если цена на товар составляла 200 рублей, а затем увеличилась до 250 рублей, то разность между ними будет равна 50 рублям. Это помогает оценить изменение стоимости товара и принять решения по поводу ценообразования и маркетинговой стратегии.

В геометрии разность используется для вычисления разницы между длинами сторон или углами. Например, для нахождения разности двух углов нужно вычесть из большего угла меньший. Это позволяет определить, насколько один угол больше или меньше другого и провести соответствующие измерения и расчеты.

ПримерВычисление разности

Доход	1000 рублей
Расходы	500 рублей
Разность	500 рублей

Таким образом, разность имеет много практических применений и помогает нам решать различные задачи в разных областях знаний.

Разность чисел в первом классе

В первом классе дети изучают понятие разности чисел до 10. Например, если у нас есть число 7 и мы отнимаем от него число 3, то разность будет равна 4 (7 — 3 = 4).

Для более наглядного представления разности чисел в первом классе применяются различные игры и упражнения. Например, детям предлагается решить задачку: «У Маши было 8 яблок, она съела 3. Сколько яблок осталось у Маши?» Дети должны будут вычислить разность чисел (8 — 3 = 5) и дать правильный ответ — у Маши осталось 5 яблок.

Понимание и умение вычислять разность чисел в первом классе является важным этапом в освоении математических навыков. Это помогает детям развивать логическое мышление, аналитические способности и умение решать простые задачи.

Использование игр и практических заданий помогает детям запомнить правила вычисления разности чисел и применять их на практике.

Подготовка к изучению разности

Перед тем, как мы начнем изучать понятие разности в математике, необходимо подготовиться и ознакомиться с некоторыми базовыми понятиями. Это поможет нам лучше понять и освоить новый материал.

Во-первых, важно хорошо знать арифметические операции: сложение и вычитание. Разница это результат вычитания двух чисел, поэтому необходимо уметь правильно вычислять разность. Если мы знаем, что разность это отнимание одного числа от другого, то сможем легко справиться с этой задачей.

Во-вторых, необходимо уметь работать с числами и считать в уме. Чтобы изучать разность чисел, нужно иметь представление о том, как выглядят числа и как они устроены. Знание числового ряда и навык счета помогут нам легко определить разность между двумя числами.

Наконец, важно понимать, что разность может быть как положительной, так и отрицательной. В зависимости от величины и расположения чисел на числовой оси, разность может быть положительной (если первое число больше второго) или отрицательной (если первое число меньше второго).

Таким образом, подготовка к изучению разности включает знание арифметических операций, умение считать в уме и понимание особенностей разности между числами. Если вы уверены в своих навыках и понимаете эти понятия, то готовы приступить к изучению разности в математике.

Ошибки при вычислении разности

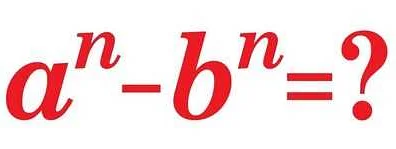
ОшибкаОбъяснение

Перепутывание порядка вычитания	Очень часто дети перепутывают порядок вычитания и вычитают из большего числа меньшее. Например, вместо вычитания 8 — 3 они могут написать 3 — 8.
Ошибки в вычислениях	Дети могут допускать ошибки при вычислении разности, особенно при работе с большими числами или сложных выражениях. Например, они могут неправильно выполнить промежуточные вычисления или сложить числа вместо их вычитания.
Неправильное использование знаков	Дети могут неправильно использовать знаки при вычитании. Например, они могут забыть поставить знак «-» перед числом или знак «=» после вычисления.

Важно помнить, что вычисление разности требует внимания и аккуратности. Чтобы избежать ошибок, рекомендуется внимательно проверять каждый шаг вычисления и использовать различные методы проверки, например, проводить обратное вычисление или использовать другие операции для подтверждения правильности ответа.

Вопрос-ответ:

Как объяснить разность в математике 1 класс?

Разность в математике — это результат вычитания одного числа из другого. Например, разность чисел 7 и 3 равна 4, так как 7 — 3 = 4. Разность можно представить как расстояние между двумя значениями.

Какие примеры разности можно привести из повседневной жизни?

В повседневной жизни можно привести множество примеров разности. Например, если у вас было 10 яблок, а вы съели 3, то разность будет равна 7. Если у вас было 15 шариков, а вы отдале 8 другу, то разность будет равна 7. В обоих случаях мы вычитаем одно число из другого, чтобы найти разность.

Как можно представить разность на числовой оси?

Разность можно представить на числовой оси, используя отрезки. Например, если есть точка A на числовой оси, которая представляет число 5, и точка B, которая представляет число 2, то разность между ними будет равна отрезку AB. Длина этого отрезка будет равна разности чисел 5 и 2, то есть 3.

Могут ли числа быть отрицательными при вычислении разности?

Да, числа могут быть отрицательными при вычислении разности. Например, если вы вычитаете число 5 из числа 2, то получите отрицательное число -3. Это значит, что разность между 2 и 5 равна -3. В таких случаях разность можно представить как направление движения на числовой оси.

Как можно использовать разность в повседневной жизни?

Разность можно использовать в повседневной жизни для решения различных задач. Например, если у вас есть определенная сумма денег, и вы хотите купить несколько товаров, то можно вычислить разность между суммой денег и стоимостью товаров, чтобы узнать, сколько денег у вас останется. Также разность можно использовать для измерения изменений величин, например, сколько килограммов веса потерял человек за неделю.

Что такое разность в математике? Как она определяется?

Разность — это результат вычитания одного числа из другого. Она определяется путем вычитания одного числа (вычитаемого) из другого числа (уменьшаемого).

Видео по теме: