Разрядная единица в математике что это
Содержимое
- 1 Разрядная единица в математике что это
Разрядная единица в математике – это понятие, которое определяет позицию цифры в числе и ее вклад в общую стоимость числа. Разрядная единица имеет значение, определяющее количество умножений числа на 10 в зависимости от ее позиции. Узнайте больше о разрядных единицах и их роли в математике.
Разрядная единица — это понятие, которое широко используется в математике для представления чисел. Она является основой для составления и понимания числовых значений, а также выполняет важную роль при выполнении арифметических операций.
Разрядная единица представляет собой позицию, которую занимает цифра в числе. Каждая цифра в числе имеет свой разряд, начиная с самого младшего (правого) разряда и продолжая до самого старшего (левого) разряда. Каждый разряд имеет свою степень десяти, которая определяет его весовой коэффициент.
Например, в числе 425, цифра 5 занимает самый младший (правый) разряд и имеет весовой коэффициент 1. Цифра 2 занимает средний разряд и имеет весовой коэффициент 10. Цифра 4 занимает самый старший (левый) разряд и имеет весовой коэффициент 100.
Разрядная единица позволяет представить числа любого размера и выполнить с ними арифметические операции. Она обеспечивает структуру числа и позволяет нам понимать его внутреннюю организацию. Благодаря разрядной единице мы можем узнать, что число 425 состоит из 4 сотен, 2 десятков и 5 единиц.
Понятие разрядной единицы

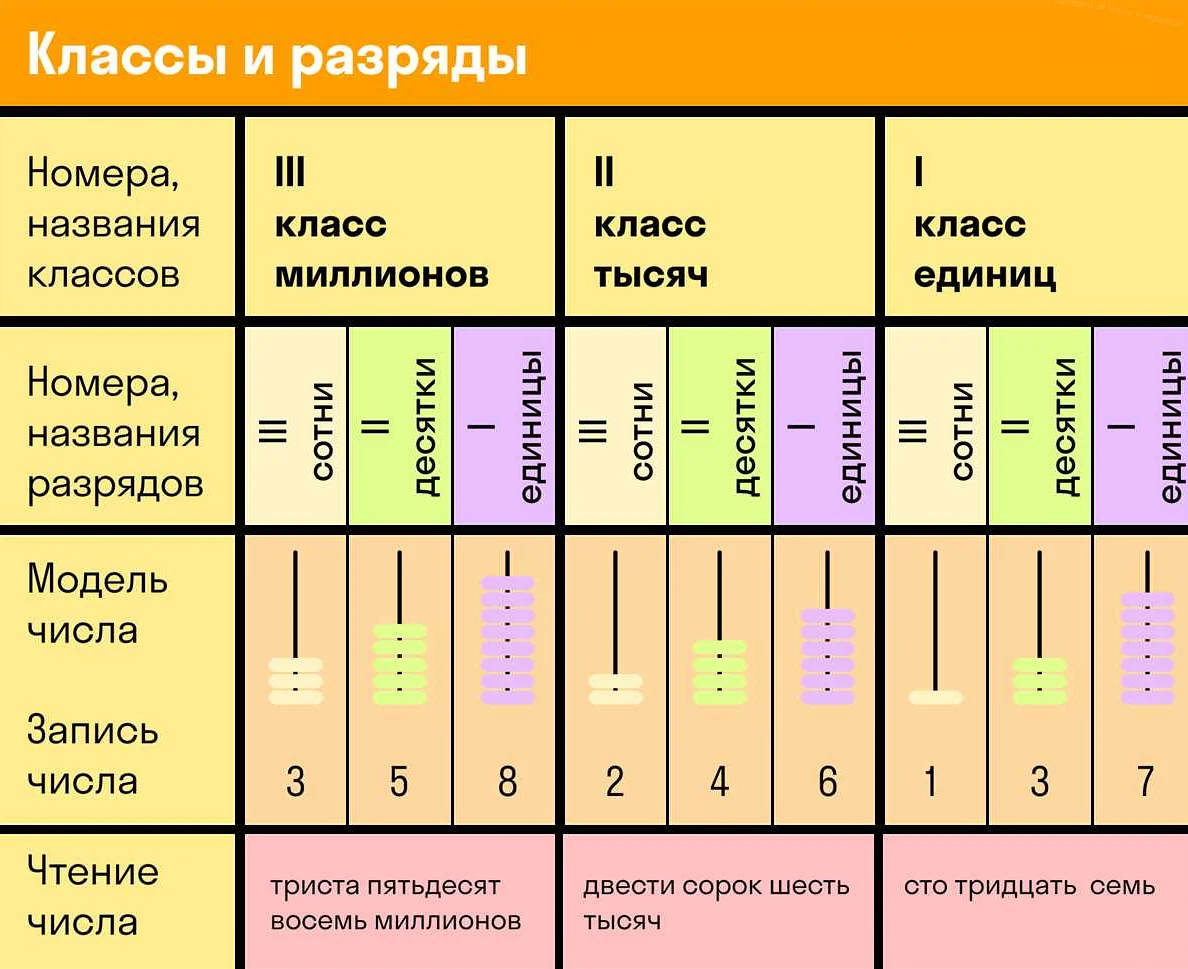
В десятичной системе счисления, самая правая позиция числа называется единицами, следующая — десятки, потом сотни, тысячи и так далее. Каждая разрядная единица умножается на соответствующую степень числа 10.
Например, в числе 12345 разрядные единицы представлены следующим образом:
- Единицы: 5
- Десятки: 4
- Сотни: 3
- Тысячи: 2
- Десятки тысяч: 1
Каждая разрядная единица имеет свое значение в зависимости от своей позиции в числе. Например, если число имеет 5 в разряде единиц, это означает, что оно состоит из пяти единиц. А если в разряде тысяч стоит число 2, это означает, что число состоит из двух тысяч.
Понимание позиции разрядной единицы в числе помогает выполнять операции с числами, такие как сложение, вычитание, умножение и деление. Без понимания разрядной единицы, сложение или вычитание чисел становится затруднительным.
Видео по теме:
Система счисления и разрядность

Система счисления представляет собой метод записи чисел, основанный на определенном наборе символов, называемых цифрами. Каждая цифра имеет свое значение, и путем комбинирования цифр можно представить любое число.
В различных системах счисления используются разные наборы цифр. Наиболее распространенными системами счисления являются десятичная система (основанная на цифрах от 0 до 9), двоичная система (основанная на цифрах 0 и 1) и шестнадцатеричная система (основанная на цифрах от 0 до 9 и буквах A-F).
Разрядность числа в системе счисления определяет количество разрядов (цифр), которые могут быть использованы для представления числа. Каждый разряд имеет свою позицию и свое значение, которое определяется основанием системы счисления и позицией разряда.
Например, в десятичной системе счисления число 1234 имеет разрядность 4, так как оно состоит из четырех разрядов: тысяч, сотен, десятков и единиц. В двоичной системе счисления число 101 имеет разрядность 3, так как оно состоит из трех разрядов: двоичных разрядов, которые могут иметь значения 0 или 1.
Разрядная единица в математике означает позицию разряда, начиная с самого младшего разряда (обычно единицы) и увеличиваясь на единицу с каждым более старшим разрядом. Каждая позиция разряда имеет значение, равное основанию системы счисления, возведенному в степень позиции разряда.
Например, в десятичной системе счисления позиция разряда единиц имеет значение 10^0 = 1, позиция разряда десятков имеет значение 10^1 = 10, позиция разряда сотен имеет значение 10^2 = 100 и т.д. Таким образом, число 1234 можно записать как 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0.
Разрядность числа в системе счисления влияет на его представление и возможные операции с ним. Чем больше разрядность числа, тем больше чисел можно представить в данной системе счисления. Однако, увеличение разрядности также влечет за собой увеличение потребляемой памяти и сложность вычислений.
Как работает разрядная единица
Например, в числе 352, число 3 находится в разряде сотен, число 5 — в разряде десятков, а число 2 — в разряде единиц. Значение каждого разряда определяется умножением цифры на соответствующую разрядную единицу и сложением полученных произведений.
Например, значение числа 352 можно вычислить следующим образом: 3 * 100 (разряд сотен) + 5 * 10 (разряд десятков) + 2 * 1 (разряд единиц) = 300 + 50 + 2 = 352.
В двоичной системе разрядная единица равна 2 в степени, равной порядку разряда. Например, в числе 1011, число 1 находится в разряде восьмерок (2 в степени 3), число 0 — в разряде четверок (2 в степени 2), число 1 — в разряде двоек (2 в степени 1) и число 1 — в разряде единиц (2 в степени 0). Значение числа 1011 вычисляется по формуле: 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 8 + 0 + 2 + 1 = 11.
Разрядные единицы играют важную роль в математике и информатике, так как позволяют представлять и обрабатывать числа различных порядков и с разным количеством разрядов.
Вопрос-ответ:
Что такое разрядная единица в математике?
Разрядная единица в математике — это позиционная система счисления, в которой каждая цифра имеет свой вес, зависящий от ее положения в числе.
Как работает разрядная единица в математике?
В разрядной единице каждая цифра в числе имеет свой вес, который равен степени основания системы счисления, возведенной в соответствующую позицию цифры. Например, в десятичной системе счисления вес цифры 3 в числе 345 будет равен 10^2, то есть 100.
Какие примеры разрядных единиц можно найти в математике?
Примеры разрядных единиц можно найти в различных системах счисления, таких как двоичная (вес каждой цифры равен 2 в соответствующей позиции), восьмеричная (вес каждой цифры равен 8 в соответствующей позиции) и шестнадцатеричная (вес каждой цифры равен 16 в соответствующей позиции).
Как разрядная единица влияет на запись и чтение чисел?
Разрядная единица определяет положение и вес каждой цифры в числе. Это позволяет записывать и читать числа большей разрядности и более компактно представлять большие числа.
В каких областях применяется разрядная единица в математике?
Разрядная единица широко применяется в различных областях, таких как компьютерные науки, электроника, телекоммуникации и финансовая математика. В компьютерных науках, например, разрядная единица используется для представления чисел в двоичной системе счисления.
Примеры разрядной единицы
Разрядная единица в математике используется для обозначения позиции числа в числовой системе. Она позволяет разделить число на отдельные разряды и определить значение каждого разряда. Рассмотрим несколько примеров разрядной единицы:
РазрядПримерЗначение
| Единицы | 123 | 3 |
| Десятки | 123 | 2 |
| Сотни | 123 | 1 |
| Тысячи | 12345 | 4 |
| Десятки тысяч | 12345 | 3 |
| Сотни тысяч | 12345 | 2 |
Каждая позиция числа имеет свое значение в зависимости от того, в каком разряде она находится. Например, в числе 12345, цифра 3 обозначает количество десятков тысяч, а цифра 4 — количество тысяч.
Использование разрядной единицы позволяет более удобно работать с большими и сложными числами, а также выполнять различные математические операции с ними.
Важность разрядной единицы

Без разрядной единицы нам было бы крайне сложно работать с большими числами. Например, представьте, что у нас есть число 123456789. Без разрядной единицы мы бы не знали, какие цифры входят в это число и как их правильно интерпретировать.
Разряды числа помогают нам определить, какой вес имеет каждая цифра в числе. Например, в числе 123456789, цифра 1 имеет вес 100 000 000, цифра 2 имеет вес 10 000 000, и так далее. Это позволяет нам проводить различные операции с числами, такие как сложение, вычитание, умножение и деление, а также упрощает чтение и запись чисел.
Разрядная единица также позволяет нам работать с отрицательными числами и десятичными дробями. Например, в числе -123.45, минус означает отрицательное число, а точка разделяет целую и десятичную части числа.
Необходимо понимать, что разрядная единица является основой для понимания и работы с числами. Она позволяет нам строить сложные вычисления, решать задачи из различных областей науки и техники, а также использовать математику в повседневной жизни.
Арифметические операции с разрядной единицей
Разрядная единица в математике представляет собой число, состоящее из цифр, разделенных на разряды. При выполнении арифметических операций с разрядной единицей, необходимо учитывать особенности этой системы.
При сложении разрядных единиц необходимо складывать цифры в каждом разряде, начиная с младшего разряда и двигаясь в старшие разряды. Если сумма цифр превышает 9, то в результате сложения в данном разряде записывается только последняя цифра, а единица переносится в следующий разряд.
Например, при сложении 123 и 987, в младшем разряде сумма будет 10 (3 + 7), записываем цифру 0 и переносим единицу в разряд десятков, в результате получаем 10 + 8 = 18. Записываем цифру 8 и переносим единицу в разряд сотен, в итоге получаем 1 + 1 = 2. Таким образом, результат сложения 123 и 987 будет равен 1110.
При выполнении вычитания разрядных единиц также необходимо учитывать переносы. Если цифра в уменьшаемом разряде меньше цифры в вычитаемом разряде, необходимо занимать единицу у следующего разряда. В противном случае, вычитаем нужное число из цифры уменьшаемого разряда.
Например, при вычитании 987 из 1234, в младшем разряде получаем 4 — 7, так как 4 меньше 7, необходимо занять единицу у разряда десятков. Затем, 3 — 8, так как 3 меньше 8, занимаем единицу у разряда сотен. Результат вычитания будет равен 247.
При умножении разрядных единиц необходимо учитывать, что произведение двух цифр в разряде может быть двузначным. В этом случае, записываем последнюю цифру произведения в данном разряде, а десятки переносим в следующий разряд.
Например, при умножении 123 и 987, получаем произведение по разрядам: первый разряд — 7 * 3 = 21, записываем 1 и переносим 2 в разряд десятков. Далее, второй разряд — 8 * 3 + 9 * 2 = 42, записываем 2 и переносим 4 в разряд сотен. И, наконец, третий разряд — 9 * 3 = 27. Результат умножения будет равен 121,701.
При делении разрядных единиц необходимо учитывать, что деление может привести к остатку. В этом случае, остаток записывается в текущий разряд, а остаток переносится в следующий разряд для дальнейшего деления.
Например, при делении 1234 на 987, получаем разность по разрядам: первый разряд — 1 / 9 = 0, остаток 1 переносим в разряд десятков. Далее, второй разряд — 12 / 9 = 1, остаток 3 переносим в разряд сотен. И, наконец, третий разряд — 34 / 9 = 3, остаток 7. Результат деления будет равен 1,253.
Таким образом, при выполнении арифметических операций с разрядной единицей необходимо учитывать особенности сложения, вычитания, умножения и деления в этой системе. Это позволяет правильно выполнять операции и получать верные результаты.
Применение разрядной единицы
Применение разрядной единицы в математике позволяет выполнять арифметические операции с числами разной длины. Например, при сложении двух чисел, каждый разряд складывается независимо от других разрядов. Это позволяет упростить процесс вычислений и облегчить работу с большими числами.
Также разрядная единица широко применяется в компьютерных системах. В компьютерах информация хранится и обрабатывается в виде двоичных чисел. Каждый бит – это разрядная единица, которая может принимать значения 0 или 1. С помощью разрядной единицы можно представить любые данные, начиная от чисел и заканчивая символами и графикой.
В цифровых системах связи, таких как Ethernet, разрядная единица используется для передачи и приема данных. Биты передаются последовательно, один за другим, и каждый бит является разрядной единицей. Это позволяет передавать большое количество информации с высокой скоростью и надежностью.
Использование разрядной единицы имеет широкий спектр применений и является неотъемлемой частью современной технологии и математики. Разрядная единица помогает сделать вычисления более эффективными и удобными, а также обеспечивает передачу данных в различных сферах деятельности.

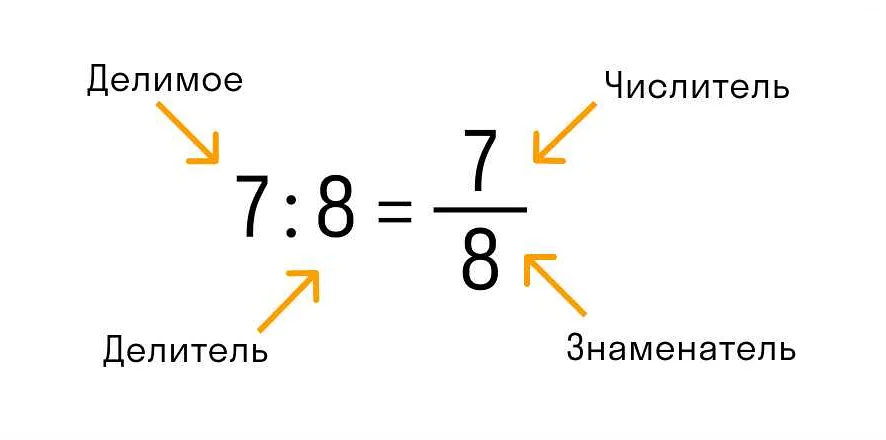

Статья очень понятно и доступно объясняет, что такое разрядная единица в математике. Я всегда думала, что цифры просто стоят рядом друг с другом, а теперь я понимаю, что каждая цифра имеет свою позицию и значение. Благодаря этой системе мы можем работать с большими числами, не запутываясь. Теперь мне понятно, почему каждая разрядная единица имеет свое название — единицы, десятки, сотни и т.д. И мне понравилось, как автор пошагово объяснил, как считать и записывать числа в разрядной системе. Теперь я чувствую себя более уверенно в работе с числами и понимаю, что разрядная единица — это нечто большее, чем просто цифра. Спасибо за понятное объяснение!
Интересная статья! Очень четко и ясно объяснено, что такое разрядная единица в математике и как она работает. Раньше я слышал о разрядах, но не знал, как они связаны с числами. Теперь стало понятно, что каждая цифра в числе находится в определенном разряде и имеет свое значение в зависимости от позиции. Также интересно узнать, что при увеличении числа на один разряд, оно становится в десять раз больше. Это поможет мне лучше понять и работать с большими числами. Спасибо за информацию!