Разрядные слагаемые в математике: что это такое и как с ними работать?

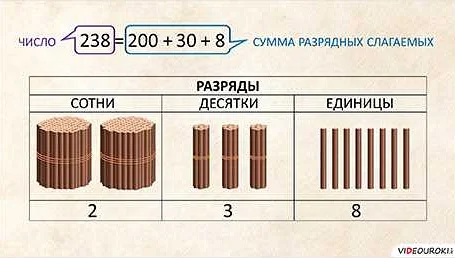
Разрядные слагаемые — это числа, которые складываются по разрядам с целью упрощения вычислений. В математике использование разрядных слагаемых позволяет легко производить сложение, вычитание, умножение и деление больших чисел, повышая точность и скорость расчетов. Узнайте, как применять разрядные слагаемые в своих вычислениях и сделайте математику проще и удобнее!

В математике разрядными слагаемыми называются числа, которые разделены на отдельные разряды в цифровом представлении. Например, число 1234567 состоит из разрядных слагаемых 1, 2, 3, 4, 5, 6 и 7. Такое представление чисел играет важную роль в математике и является основой для работы с системами счисления, арифметических операций и многих других математических концепций.

Одной из основных операций с разрядными слагаемыми является сложение. Для сложения разрядных слагаемых необходимо учитывать разряд каждой цифры. Например, при сложении чисел 123 и 456 мы сначала складываем цифры в единицах (3 и 6), затем числа в десятках (2 и 5) и, наконец, числа в сотнях (1 и 4). Результат сложения будет равен 579.

В статье мы рассмотрим более подробно принципы сложения разрядных слагаемых в математике и покажем, как эта концепция используется в системах счисления и других математических операциях.

Разрядные слагаемые: суть и примеры

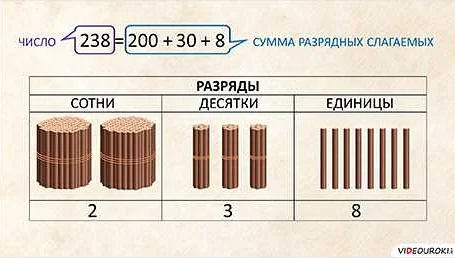
Разрядные слагаемые — это числа, записанные в разрядной форме, которые складываются по разрядам. Для сложения двух чисел сначала складываются цифры в одном разряде, затем переносятся в следующий разряд и складываются там.

Например, чтобы сложить числа 23 и 47, сначала складываем числа в разряде единиц (3+7=10), записываем ноль и переносим единицу в разряд десятков. Затем складываем числа в разряде десятков (2+4+1=7) и получаем ответ 70.

Еще один пример — сложение чисел 345 и 678. Сначала складываем числа в разряде единиц (5+8=13), записываем 3 и переносим единицу в разряд десятков. Затем складываем числа в разряде десятков (4+7+1=12), записываем 2 и переносим единицу в разряд сотен. В разряде сотен складываем числа (3+6+1=10), записываем 0 и переносим единицу в разряд тысяч. Итоговое число — 1023.

Разрядные слагаемые используются не только для сложения чисел, но и для других математических операций, например, умножения.

Видео по теме:

Что такое разрядные слагаемые?

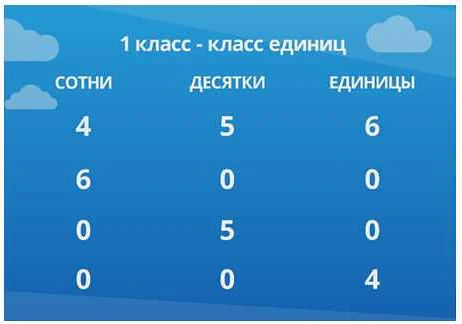
В математике разрядными слагаемыми называются числа, которые имеют одинаковые разряды в позиционной системе счисления. Разрядом называется элементарное место в числе, которое соответствует определенной степени числа основания системы счисления.

Например, в десятичной системе счисления разряды обозначаются единицами, десятками, сотнями, тысячами и т.д. В двоичной системе счисления разрядами являются единицы, двойки, четверки, восьмерки и т.д.

Разрядные слагаемые используются в математических операциях, таких как сложение и вычитание. Например, в числе 1234 разрядные слагаемые это 1000, 200, 30 и 4. При сложении двух чисел, разрядные слагаемые складываются по соответствующим разрядам, начиная с наименьшего.

Разрядные слагаемые также имеют практическое применение в различных областях, таких как компьютерная наука, криптография, статистика и экономика.

Почему важно знать, как складывать разрядные слагаемые?

Разрядные слагаемые — это числа, в которых каждая цифра занимает свое определенное место в числе и обладает своим весом. Знание правил сложения разрядных слагаемых является основой для решения многих математических задач, таких как вычисление суммы платежей по кредиту, нахождение среднего значения различных величин и т.д.

Кроме того, знание правил сложения разрядных слагаемых играет важную роль в повседневной жизни. Часто мы сталкиваемся с необходимостью складывать большие числа, которые состоят из множества разрядов. Например, если вы хотите посчитать стоимость всех товаров в корзине, вам нужно сложить цены на каждый товар. Часто цены на товары состоят из многих разрядов, поэтому знание правил сложения разрядных слагаемых поможет вам быстро и эффективно решить данную задачу.

Кроме того, знание правил сложения разрядных слагаемых полезно для развития математической логики и мышления в целом. Логические операции при сложении разрядных слагаемых направляют нас на решение задачи в более строго упорядоченном порядке, что способствует развитию нашей умственной деятельности.

Таким образом, знание правил сложения разрядных слагаемых является необходимым для успешного решения многих математических задач и имеет практическое применение в повседневной жизни. Кроме того, это является важной составляющей развития нашей математической логики и мышления в целом.

Правила складывания разрядных слагаемых

Разрядным слагаемым называется число, которое записано в разряде соответствующей величины. Например, в числе 457, 4 — это разрядная цифра сотен, 5 — десятков, 7 — единиц. При складывании разрядных слагаемых необходимо придерживаться следующих правил:

1. Выравнивание слагаемых. Перед сложением разрядных слагаемых необходимо выровнять их в соответствии с числами разрядов. Например, если мы складываем числа 472 и 36, то перед сложением мы выровняем цифры «4» и «3», записав 036 и 472.
2. Сложение единиц. Сложение единиц происходит путем сложения чисел в последнем разряде. Например, в числах 964 и 375 мы сложим 4 и 5, получим 9 и запишем единицы (0) ниже.
3. Перенос десятков. Если в результате сложения единиц получилось число больше 9, необходимо записать единицы и перенести десятки на следующий разряд. Например, при сложении чисел 964 и 375, мы получили 9 в единицах, записали 0 и перенесли 1 на десятки.
4. Сложение десятков. Далее, мы складываем десятки соответствующих разрядов. При этом учитываем переносы из предыдущего разряда. Например, в числах 964 и 375 мы сложим 6, 7 и 1 (перенос) и получим 14. Запишем 4 и перенесем 1 на сотни.
5. Сложение сотен. Далее, складываем сотни соответствующих разрядов, учитывая переносы. Например, в числах 964 и 375 мы сложим 9, 5 (перенос) и 3, получим 17. Запишем 7 и перенесем 1 на разряды тысяч.
6. Запись результата. В результате сложения разрядных слагаемых мы получаем число, которое записываем справа налево, перенося при необходимости единицы на старшие разряды.

Как сложить разрядные слагаемые одинакового разряда

Разрядные слагаемые – это числа, которые записываются по разрядам, начиная с единиц и заканчивая старшим разрядом. Каждый разряд имеет свой вес, который равен 10 в степени номера разряда.

Для сложения разрядных слагаемых одинакового разряда необходимо их просто сложить. Например, чтобы сложить числа 3456 и 6789, нужно сначала сложить единицы (6 и 9), получая 15. Так как 15 больше 10, переносим 1 в следующий разряд (т.е. в десятки), а записываем в разряд единиц число 5. Затем складываем десятки (5 и 8), к результату прибавляем перенос 1, и получаем 14. Снова переносим единицу в следующий разряд (т.е. в сотни), а записываем в разряд десятков число 4. Таким образом, получаем число 10245.

Обратите внимание, что если разрядные слагаемые не имеют одинакового разряда, то перед сложением необходимо выполнить дополнительные операции, включая добавление нулей в соответствующие разряды.

Например, чтобы сложить 836 и 24, необходимо добавить ноль в разряд десятков у числа 24 (т.е. записать его как 024), а затем уже сложить (8+0=8; 3+2=5; 6+4=10; переносим 1 в разряд сотен, а записываем в разряд десятков число 0). В итоге получаем число 860.

Как сложить разрядные слагаемые разного разряда:

Когда слагаемые имеют разный разряд, нужно начинать складывать слагаемые с меньшего разряда и постепенно переходить к более крупным разрядам. Нужно примерно так:

1. Расположите слагаемые вертикально с совпадающими разрядами под горизонтальной чертой.
2. Сложите последние разряды в столбик. Если получается число больше 9, запомните единицу и записывайте только однозначный результат.
3. Сложите разряды второго порядка. Если запомнили единицу в предыдущем шаге, прибавьте ее к следующей сумме и сложите все числа в столбик. Если результат больше 9, запомните единицу и опять записывайте только однозначную цифру.
4. Продолжайте сложение пока не дойдете до наибольшего разряда. Если прибавляете запомненную единицу, то не забудьте ее учесть.
5. Если одно из слагаемых закончилось раньше, то продолжите сложение оставшегося слагаемого с последней запомненной единицей.

Например, чтобы сложить 123 и 45, нужно начать со сложения последнего разряда: 3 + 5 = 8. Далее слагаемые станут 12 и 4, сложим их: 2 + 4 = 6, добавляем запомненную единицу (1) и получаем 7. Наконец, слагаемые станут 1 и 0, добавляем запомненную единицу (1) и получаем 2. Итого, 123 + 45 = 168.

Примеры сложения разрядных слагаемых

Разрядные слагаемые — это числа, состоящие из разрядов, которые не пересекаются. Чтобы сложить два разрядных слагаемых, нужно сложить цифры на соответствующих разрядах. Разберем несколько примеров.

Пример 1: 1234 + 5678 = 6912. Здесь слагаемые 1234 и 5678 разбиты на разряды, и мы складываем цифры на каждом разряде: 4 + 8 = 12 (пишем 2 и запоминаем 1), 3 + 7 + 1 (запомненная единица) = 11 (пишем 1 и запоминаем 1), 2 + 5 + 1 = 8, 1 + 6 = 7. Получаем число 6912.

Пример 2: 587 + 279 = 866. Здесь на младшем разряде складываем 7 и 9, получаем 16 (пишем 6 и запоминаем 1), на следующем разряде складываем 8, 7 и запомненную единицу, получаем 16 (пишем 6 и запоминаем 1), на старшем разряде складываем 5 и запомненную единицу, получаем 6. Итого 866.

• Важно: при сложении разрядных слагаемых необходимо запоминать перенос на следующий разряд в том случае, когда сумма цифр на текущем разряде превышает 9.
• Внимание: при сложении разрядных слагаемых важно, чтобы числа были одинакового разряда, в противном случае необходимо добавить нули слева до одинакового разряда.

Пример 3: 102 + 4567 = 4679. Здесь мы добавляем ноль слева к числу 102, чтобы оно имело четыре разряда. Затем можно выполнить сложение как в примере 1.

Пример 4: 2398 + 75 = 2473. Записываем число 75 с нулями слева, чтобы оно имело 4 разряда. Затем можно выполнить сложение как в примере 1.

Итог: сложение разрядных слагаемых не сложно, если следовать правилам и запоминать перенос на следующий разряд. Кроме того, важно приводить числа к одному разряду, добавляя нули слева.

Сложение в столбик двузначных чисел

Сложение в столбик двузначных чисел – одна из основных операций, которую нужно знать и уметь выполнять в математике. Для сложения двузначных чисел используется метод столбикового сложения. Он заключается в том, что все цифры сходных разрядов записываются в один столбец, а сложение выполняется последовательно, начиная с младших разрядов.

Для начала нужно поставить два числа так, чтобы единицы и десятки были напротив друг друга. Затем нужно сложить соответствующие разряды, начиная с единиц, и выполнить перенос на следующий разряд, если сумма больше десяти.

Пример:

43

+ 25

—-

Сначала складываем единицы: 3+5=8, на следующем разряде получаем 4+2=6. Ответ: 68.

Если в процессе сложения получается число больше 99, то нужно выполнить перенос на разряд десятков. Например:

37

+ 68

—-

105

Сначала сложим единицы: 7+8=15, получаем 5 и перенос 1. Затем складываем десятки и прибавляем перенос: 3+6+1=10. Получаем 105.

Столбиковое сложение – это простой и удобный способ выполнения операций с числами. Попробуйте его использовать для сложения двузначных чисел и вы увидите, как это просто и быстро.

Сложение в столбик трехзначных чисел

Сложение в столбик является одним из основных методов выполнения математических операций и может применяться для складывания чисел любой длины. В данном случае будут рассмотрены трехзначные числа, которые складываются в столбик.

Для начала переносим единицы из разряда справа на разряд слева и складываем их вместе. Затем переносим десятки и также складываем их вместе. После этого переносим сотни и снова складываем их. В конечном итоге получаем сумму заданных трехзначных чисел.

Например, для складывания чисел 567 и 358 следует провести следующие операции:

5	6	7
+
3	5	8
—	—	—
8	1	5

Таким образом, рассмотренный метод сложения в столбик трехзначных чисел довольно прост и может быть легко освоен школьниками на начальных этапах изучения математики.

Применение разрядных слагаемых в математических задачах

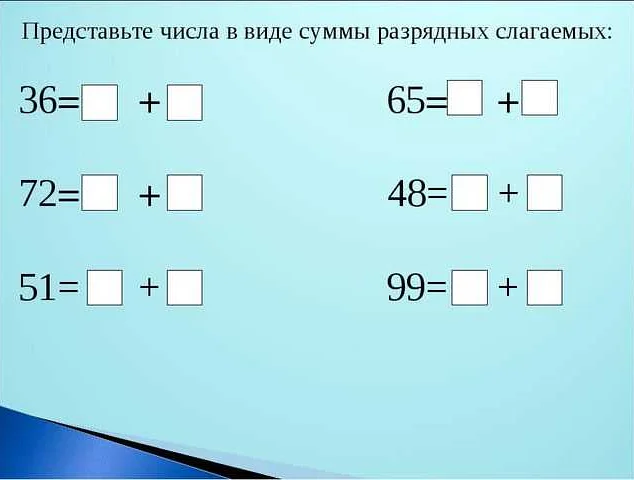
Разрядные слагаемые могут быть использованы для решения различных математических задач, особенно в задачах, связанных с десятичной системой счисления и делением на множители.

Одним из наиболее распространенных примеров является разложение числа на разрядные слагаемые при вычислении произведения двух многоразрядных чисел в столбик. При этом каждое число записывается в виде суммы разрядных слагаемых, а затем произведение находится путем перемножения всех возможных пар слагаемых и сложения соответствующих произведений.

Также разрядные слагаемые могут быть использованы для решения задач на деление на множители. При этом число разбивается на разрядные слагаемые, а затем каждый слагаемый проверяется на делимость на множитель.

Другой пример использования разрядных слагаемых — это разложение числа на множители. При этом число записывается в виде суммы разрядных слагаемых, а затем каждый слагаемый проверяется на делимость на простое число и используется для построения разложения на множители.

Таким образом, использование разрядных слагаемых является удобным и эффективным способом для решения различных математических задач, особенно связанных с десятичной системой счисления и делением на множители.

Задачи на пополнение до 100

Разрядные слагаемые очень важны для решения задач на пополнение до 100. К примеру, если мы знаем, что 62 + 38 = 100, то мы можем легко решить задачу, где нужно дополнить число до 100. Например, сколько нужно добавить к числу 57, чтобы получилось 100? Очевидно, что нам надо добавить 43.

Другая задача на пополнение до 100 может звучать так: Бабушка купила 37 конфет, а внук еще 55. Сколько еще конфет им нужно купить, чтобы получилось 100? В данном случае нам нужно найти разрядное слагаемое для числа 92, чтобы получилось 100. Ответ: 8.

Задачи на пополнение до 100 могут быть гораздо сложнее, например, если мы знаем, что 37 + 14 + ? = 100, то нам нужно найти разрядное слагаемое для числа 49. В общем случае, чтобы найти разрядное слагаемое для числа X, нам нужно вычислить разницу между X и 100. Например, если X = 72, то нужное слагаемое равно 28 (100 — 72 = 28).

Важно понимать, что задачи на пополнение до 100 могут быть как сложными, так и простыми. Однако, при решении любых таких задач важно правильно использовать понятие разрядных слагаемых, ведь именно это понятие позволит нам быстро и легко найти нужное число.

Задачи на разложение числа

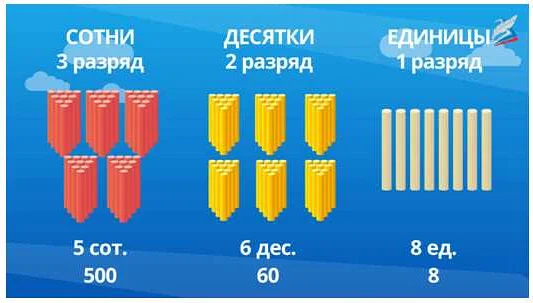
Задачи на разложение числа – это тип заданий, где требуется найти различные способы разложения заданного числа на слагаемые. Это важный навык, который помогает развивать логическое мышление, а также улучшает навыки арифметики.

Разложение числа на слагаемые может быть представлено разными способами. Например, число 6 можно представить в виде: 1+5, 2+4, 3+3 и т.д. Таким образом, есть много способов разложения чисел на слагаемые.

Задачи на разложение числа часто приходятся на государственную аттестацию по математике и поступление в вузы. Они могут быть разной степени сложности, и часто охватывают такие темы, как комбинаторика, теория чисел и арифметические операции.

• Примеры задач на разложение чисел:
  1. Разложите число 12 на простые слагаемые.
  2. Сколько существует различных способов разложения числа 10 на слагаемые?
  3. Найдите все способы разложения числа 8 на нечетные слагаемые.

Решение задач на разложение числа требует хорошего знания основных правил арифметики и умения применять их в различных ситуациях. Также важно уметь использовать логическое мышление и аналитические навыки для нахождения всех возможных вариантов разложения числа.

Вопрос-ответ:

Что такое разрядные слагаемые?

Разрядные слагаемые — это числа, записанные в разрядной форме, где каждая цифра представляет определенный разряд, например, единицы, десятки, сотни и т.д. Вследствие этого, число можно разбить на разрядные слагаемые, которые представляют собой сложение цифр, умноженных на соответствующие степени десяти. Например, число 135 может быть разложено на разрядные слагаемые: 1*100 + 3*10 + 5.

В чем разница между разрядными слагаемыми и столбиковым методом сложения?

Разрядные слагаемые и столбиковый метод сложения — это два различных подхода к сложению. В разрядных слагаемых число разбивается на цифры в соответствии с их разрядом, а в столбиковом методе сложения число записывается в столбец таким образом, чтобы цифры каждого разряда были расположены друг под другом. Основное отличие заключается в том, что в разрядных слагаемых каждая цифра умножается на степень десяти, а в столбиковом методе сложения цифры в каждом разряде складываются вместе без умножения на степень десяти.

Как складывать разрядные слагаемые?

Складывать разрядные слагаемые очень просто, так как каждая цифра умножается на соответствующую степень десяти, а затем все умноженные цифры складываются вместе. Например, чтобы сложить числа 135 и 267, нужно разложить их на разрядные слагаемые: 1*100 + 3*10 + 5 и 2*100 + 6*10 + 7. Затем каждый разряд складывается отдельно: 1*100 + 2*100 = 3*100, 3*10 + 6*10 = 9*10, 5 + 7 = 12. В результате получается число 390.

Как разложить число на разрядные слагаемые?

Чтобы разложить число на разрядные слагаемые, нужно выделить каждую цифру в соответствии с ее разрядом и умножить ее на соответствующую степень десяти. Например, чтобы разложить число 1234 на разрядные слагаемые, нужно выполнить следующие действия: 1*1000 + 2*100 + 3*10 + 4. В итоге получается разложение: 1000 + 200 + 30 + 4.

Зачем нужно использовать разрядные слагаемые?

Использование разрядных слагаемых упрощает процесс выполнения математических операций, таких как сложение и вычитание, особенно при работе с большими числами. Разбиение числа на разрядные слагаемые позволяет производить операции над числами по отдельности в каждом разряде, что делает вычисления более понятными и удобными.

Как сложить числа, записанные в разных системах исчисления?

Сложение чисел, записанных в разных системах исчисления, осуществляется по той же самой схеме, что и сложение чисел, записанных в десятичной системе. Необходимо выразить каждое число в десятичном виде, разложив его на разрядные слагаемые, затем сложить слагаемые каждого числа и вычислить сумму. Например, чтобы сложить числа 1011 (в двоичной системе исчисления) и 52 (в десятичной системе), нужно перевести число 1011 в десятичную систему, разложив его на разрядные слагаемые: 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11. Затем сложить число 11 и число 52, что даст в итоге число 63.

Как использовать разрядные слагаемые при решении уравнений и неравенств?

Разрядные слагаемые могут быть использованы при решении уравнений и неравенств путем разложения чисел на разрядные слагаемые и анализа каждого разряда отдельно. Так, например, при решении линейного уравнения ax + b = c, можно разложить число c на разрядные слагаемые и вычесть из него разрядные слагаемые чисел ax и b, получив новое уравнение, где каждый разряд складывается отдельно. Аналогично, при решении неравенств с помощью разрядных слагаемых можно определить диапазоны допустимых значений для каждого разряда и использовать их для нахождения решения.