Математика что такое разряд и классы

Разряды и классы в математике — это способ организации чисел и разделения их на группы. Разряд — это позиция цифры в числе, а класс — это группа разрядов с одинаковым значением. Понимание разрядов и классов помогает упростить арифметические операции и работу с большими числами.

Разряды и классы – важные понятия в математике, которые помогают упорядочить и классифицировать числа. Разряды определяют положение цифры в числе в зависимости от ее веса. Каждая цифра в числе занимает определенный разряд: единицы, десятки, сотни, тысячи и т.д. Разряды образуют классы, которые помогают разбить числа на группы и сделать их более удобными для работы.

Каждый разряд имеет свое значение, которое определяется его позицией относительно запятой или точки. Числа, находящиеся слева от запятой, называются целыми числами, а числа, находящиеся справа от запятой, называются десятичными дробями. Разряды в целых числах и десятичных дробях имеют различные значения и играют разные роли при выполнении математических операций.

Примеры использования разрядов и классов можно найти в различных областях математики и науки. Например, в физике разряды используются для измерения величин, таких как масса, длина, время и т.д. В программировании разряды играют важную роль при работе с числами и переменными. В экономике разряды используются для анализа и представления данных, таких как стоимость товаров и услуг, доходы и расходы.

Знание о разрядах и классах в математике является основой для понимания и решения различных задач, связанных с числами и их свойствами. Правильное использование разрядов и классов помогает упорядочить числа, выполнить математические операции, анализировать данные и делать выводы. Это незаменимые навыки не только для математиков, но и для всех, кто работает с числами в повседневной жизни.

Разряды в математике: определение и применение

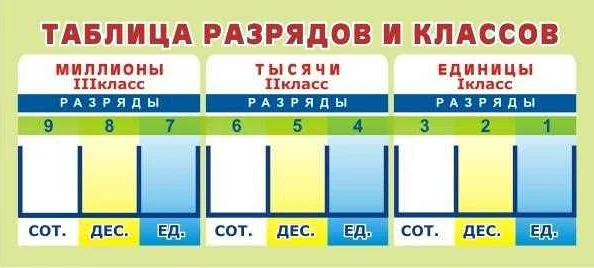
В математике разряды используются для организации чисел по разрядам и упрощения их обработки. Разряды образуются путем разбиения числа на группы, состоящие из определенного количества цифр.

Каждый разряд имеет свое значение, которое определяется позицией цифры в числе. Наиболее распространенной системой разрядов является десятичная система с основанием 10. В этой системе число разбивается на тысячные, сотые, десятые и единицы разряды, а каждый разряд имеет увеличивающуюся в 10 раз степень основания.

Применение разрядов позволяет упростить операции с большими числами. Например, при сложении и вычитании чисел, разряды выравниваются по позиции, что позволяет производить операции по каждому разряду отдельно.

Кроме того, разряды используются для округления чисел. Если требуется округлить число до определенного разряда, все цифры после этого разряда обнуляются.

Разряды также играют важную роль в представлении чисел в компьютерных системах. В двоичной системе разряды образуются по аналогии с десятичной системой, но с основанием 2. Каждый разряд в двоичной системе имеет значение, увеличивающееся в 2 раза.

Таким образом, разряды в математике играют важную роль в организации чисел и их обработке, а также в представлении чисел в различных системах счисления.

Классы в математике: основные понятия и свойства

Основное понятие класса в математике — это набор объектов, которые обладают общим свойством или характеристикой. Объекты внутри класса называются элементами класса или членами класса.

Свойства классов в математике:

СвойствоОписание

Объединение классов	Результатом объединения двух классов является новый класс, который содержит все элементы из обоих исходных классов.
Пересечение классов	Результатом пересечения двух классов является новый класс, который содержит только те элементы, которые присутствуют в обоих исходных классах.
Разность классов	Результатом разности двух классов является новый класс, который содержит только те элементы, которые присутствуют в первом классе, но отсутствуют во втором классе.
Дополнение класса	Дополнение класса — это класс, который содержит все элементы, не принадлежащие данному классу, но принадлежащие определенному универсальному множеству.

Классы в математике позволяют систематизировать объекты и проводить операции над классами, такие как объединение, пересечение, разность и дополнение. Эти операции позволяют строить новые классы, основанные на существующих классах и их свойствах.

Примеры классов в математике: класс всех четных чисел, класс всех треугольников, класс всех положительных чисел.

Изучение классов в математике позволяет более глубоко понять структуру и связи между объектами, а также проводить анализ и решать различные задачи в различных областях математики и ее приложениях.

Цифры и разряды: взаимосвязь и важность

Разряды, с другой стороны, определяют позицию цифры в числе. В десятичной системе численности разрядов равна десяти. Первый разряд, также известный как единицы, имеет наименьшее значение. Затем идут разряды десятков, сотен, тысяч и так далее. Каждый следующий разряд увеличивает значение числа в 10 раз.

Взаимосвязь между цифрами и разрядами очень важна при работе с числами. Она позволяет нам понимать, каково значение каждой цифры в числе и как их комбинация определяет общее значение числа. Например, в числе 153, цифра 1 находится в разряде сотен, цифра 5 — в разряде десятков, а цифра 3 — в разряде единиц. Эти цифры вместе образуют число сто пятьдесят три.

Знание взаимосвязи цифр и разрядов помогает нам выполнять различные операции с числами, такие как сложение, вычитание, умножение и деление. Оно также позволяет нам анализировать и сравнивать числа, чтобы понять их свойства и особенности. Понимание цифр и разрядов является фундаментальным для развития математической грамотности и расширения наших знаний в области чисел и операций с ними.

Разрядное сложение и вычитание: примеры и методика

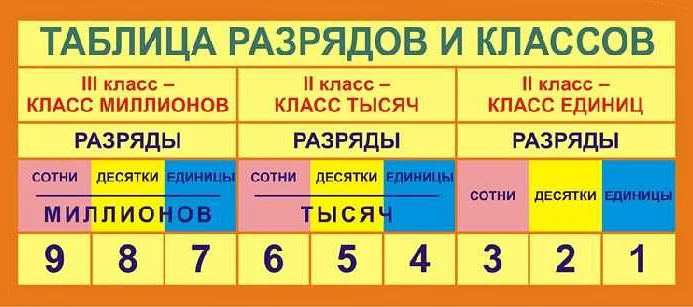
Для выполнения разрядного сложения и вычитания необходимо следовать определенной методике:

Разрядное сложение:

1. Выравнивание чисел по разрядам, начиная с единиц. Если одно число короче другого, добавляем нули в начало.

2. Складываем цифры в каждом разряде, начиная справа. Если сумма превышает 9, запоминаем единицу и записываем остаток от деления суммы на 10.

3. Переносим единицу на следующий разряд слева, если она была.

4. Продолжаем складывать разряды слева направо, учитывая перенос единицы.

Пример разрядного сложения:

1234

+ 5678

_________

6912

Разрядное вычитание:

1. Выравнивание чисел по разрядам, начиная с единиц. Если одно число короче другого, добавляем нули в начало.

2. Вычитаем цифры в каждом разряде, начиная справа. Если разность отрицательна, занимаем 10 у следующего разряда и запишаем разность.

3. Продолжаем вычитать разряды слева направо, учитывая заем.

Пример разрядного вычитания:

5678

— 1234

_________

4444

Таким образом, разрядное сложение и вычитание позволяют получать точные результаты при работе с числами разной разрядности. Эти операции являются важным инструментом в математике и широко применяются в повседневной жизни.

Классы чисел: натуральные, целые, рациональные, иррациональные

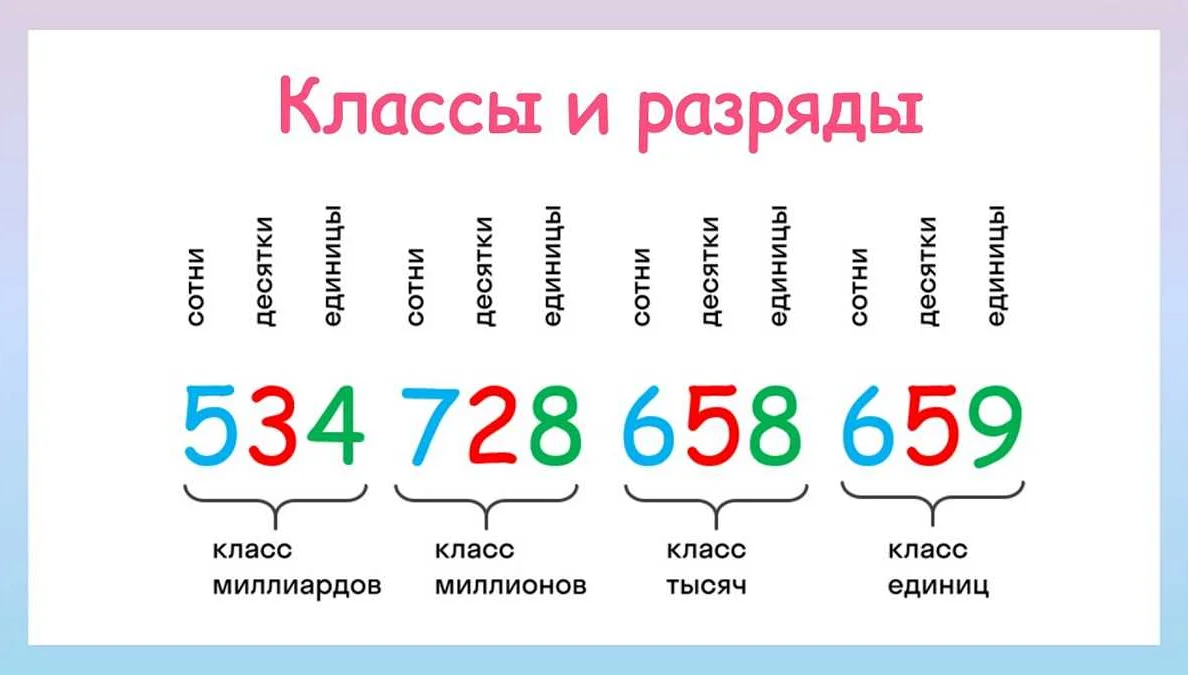
Математика изучает различные классы чисел, которые позволяют нам описывать и сравнивать разные типы числовых значений. Основные классы чисел включают натуральные числа, целые числа, рациональные числа и иррациональные числа.

Натуральные числа (обозначаются символом N) — это положительные целые числа, которые используются для подсчета и нумерации. Это множество чисел {1, 2, 3, 4, …}, которые можно использовать для счета предметов или людей.

Целые числа (обозначаются символом Z) — это расширение натуральных чисел, включающее также отрицательные числа и ноль. Это множество чисел {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}, которые могут быть использованы для представления долгов, температурных показателей и других значений в реальном мире.

Рациональные числа (обозначаются символом Q) — это числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами. Они включают в себя как натуральные, так и целые числа, а также все возможные комбинации десятичных дробей и периодических десятичных дробей. Например, 1/2, 3/4, -2/5, 0.25 и 0.333… являются рациональными числами.

Иррациональные числа (обозначаются символом I) — это числа, которые не могут быть представлены в виде дроби и имеют бесконечное число недвижущихся десятичных знаков. Они включают в себя такие числа, как корень квадратный из 2, пи (π) и экспонента (e). Иррациональные числа не могут быть точно представлены в виде десятичной дроби и требуют бесконечного числа знаков после запятой для их точного представления.

Изучение разных классов чисел позволяет нам лучше понять их свойства и использовать их в различных математических задачах. Например, рациональные числа могут использоваться для решения уравнений и задач, связанных с долями и процентами, а иррациональные числа могут использоваться для моделирования физических явлений и вычисления площадей и объемов.

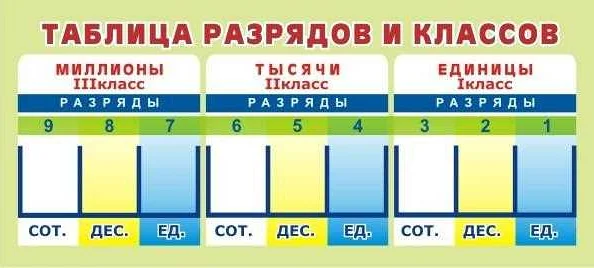
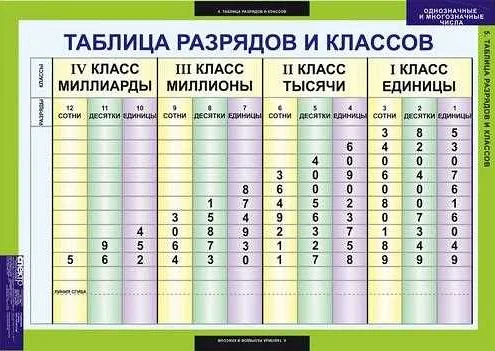
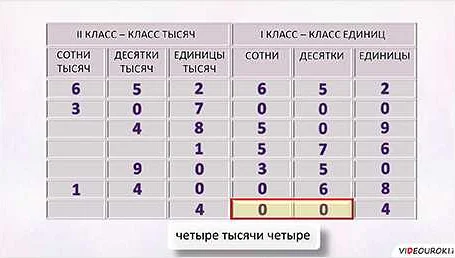
Разряды и классы в десятичной системе счисления

Разряды в десятичной системе счисления обозначают позицию каждой цифры в числе. Каждый разряд имеет определенное значение, определяемое степенью числа 10. Наименьший разряд называется единицами, следующий — десятками, затем — сотнями, тысячами, десятками тысяч и так далее. Число 895, например, имеет 3 разряда: 5 в разряде единиц, 9 в разряде десятков и 8 в разряде сотен.

Классы в десятичной системе счисления представляют группы разрядов, разделенные запятой. Каждый класс имеет определенное значение в зависимости от его позиции относительно запятой. Классы влево от запятой называются классами целой части, а классы вправо от запятой — классами десятичной части. Например, число 12,345 состоит из двух классов: класса целой части (содержит разряды 12) и класса десятичной части (содержит разряды 345).

Разряды и классы в десятичной системе счисления позволяют нам представлять и работать с числами любой величины и точности. Они являются фундаментальными понятиями в математике и играют важную роль в решении различных задач и проблем.

Видео по теме:

Вопрос-ответ:

Что такое разряды и классы в математике?

В математике, разряды и классы — это способы представления чисел в позиционной системе счисления. Разряды представляют разрядные позиции числа, а классы представляют различные значения, которые могут быть записаны в каждой позиции.

Какие свойства имеют разряды и классы в математике?

Разряды и классы имеют несколько свойств. Во-первых, разряды определяют вес или значение каждой позиции в числе. Во-вторых, классы определяют диапазон возможных значений для каждой позиции. Например, в десятичной системе классы для каждой позиции варьируются от 0 до 9. В-третьих, разряды и классы могут быть использованы для вычисления суммы, разности или произведения чисел.

Можете привести примеры разрядов и классов в математике?

Конечно! В десятичной системе разряды включают единицы, десятки, сотни и т.д. Каждая позиция имеет свой собственный класс, в котором числа могут варьироваться от 0 до 9. Например, в числе 365, 5 находится в разряде единиц, 6 — в разряде десятков и 3 — в разряде сотен.

Как разряды и классы помогают в математике?

Разряды и классы помогают нам представлять и работать с числами в позиционной системе счисления. Они позволяют нам вычислять суммы, разности и произведения чисел, а также делать другие операции, такие как возведение в степень или извлечение корня. Они также позволяют нам оценивать и сравнивать числа, определять их порядок и ранг.

Какие еще системы счисления используют разряды и классы?

Помимо десятичной системы, разряды и классы также используются в других системах счисления, таких как двоичная, восьмеричная и шестнадцатеричная. В двоичной системе разряды включают единицы, двойки, четверки и т.д., а классы варьируются от 0 до 1. В восьмеричной системе разряды включают единицы, восьмерки, шестнадцатерки и т.д., а классы варьируются от 0 до 7. В шестнадцатеричной системе разряды включают единицы, шестерки, шестнадцатерки и т.д., а классы варьируются от 0 до F.

Классы и разряды в других системах счисления: двоичная, восьмеричная, шестнадцатеричная

В математике существует несколько различных систем счисления, которые отличаются от десятичной системы, которую мы используем в повседневной жизни. В этих системах счисления также присутствуют классы и разряды, которые имеют свои особенности.

Одной из наиболее распространенных альтернативных систем счисления является двоичная система счисления. В двоичной системе счисления используются всего две цифры — 0 и 1. Классы и разряды в двоичной системе совпадают с классами и разрядами в десятичной системе, но значения цифр в разрядах могут быть только 0 или 1.

Еще одной распространенной системой счисления является восьмеричная система счисления. В восьмеричной системе счисления используются восемь цифр — от 0 до 7. Классы и разряды в восьмеричной системе также совпадают с классами и разрядами в десятичной системе.

Третьей системой счисления, рассмотренной в данной статье, является шестнадцатеричная система счисления. В шестнадцатеричной системе счисления используются шестнадцать цифр — от 0 до 9 и от A до F. Классы и разряды также совпадают с классами и разрядами в десятичной системе.

Все эти системы счисления имеют свои особенности и применяются в различных областях науки и техники. Например, двоичная система широко используется в компьютерах для представления и обработки информации, а шестнадцатеричная система применяется при программировании и работе с цифровыми устройствами.

Изучение классов и разрядов в других системах счисления помогает лучше понять принципы работы этих систем и их применение в практике. Использование различных систем счисления может быть полезным при решении математических задач и упрощении вычислений.

Разряды и классы в алгебре: мономы, полиномы, рациональные выражения

В алгебре существуют различные классы, в которых объекты имеют общие характеристики. Одним из таких классов является класс мономов. Моном представляет собой алгебраическое выражение, состоящее из произведения числового коэффициента и одночлена, в котором переменные возводятся в натуральные степени.

Примеры мономов:

• 3x
• 5xy^2
• -2a^3b^2

Другим важным классом в алгебре является класс полиномов. Полином представляет собой алгебраическое выражение, состоящее из суммы или разности нескольких мономов.

Примеры полиномов:

• 2x^2 + 3xy — 4
• 5a^3b — 2ab^2 + 7

Рациональные выражения — это алгебраические выражения, в которых числитель и знаменатель являются полиномами.

Примеры рациональных выражений:

• (x^2 + 2x + 1) / (x + 1)
• (3a^2b — 5ab + 2) / (2ab — 3)

Разряды и классы в алгебре позволяют структурировать и изучать алгебраические выражения и операции над ними. Понимание этих понятий является важной основой для дальнейшего изучения алгебры и ее применения в других областях математики и науки в целом.