Что в математике значат квадратные скобки

Квадратные скобки в математике выполняют различные функции, они могут обозначать элементы массива, границы интервала, индексы и многое другое. Узнайте, как использовать квадратные скобки в математических выражениях и формулах.

Квадратные скобки — один из основных инструментов математической нотации, используемой для обозначения различных математических объектов и операций. Эти скобки имеют свои уникальные свойства и применяются в различных контекстах, позволяя упростить и структурировать математические выражения.

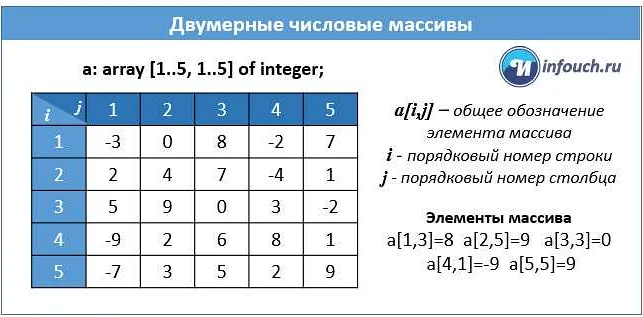
Одним из наиболее распространенных применений квадратных скобок является обозначение массивов или списков. В программировании эти скобки используются для создания и доступа к элементам массива. В математике же они применяются для обозначения множества элементов, записанных в определенном порядке. Например, [1, 2, 3] — это массив или список из трех элементов.

Кроме того, квадратные скобки широко используются для обозначения операции взятия элемента или подмножества из другого множества. Например, [a, b] означает множество, включающее элементы a и b. Если же имеется большее количество элементов, их можно разделить запятыми, например: [a, b, c].

Квадратные скобки также используются для обозначения интервалов на числовой прямой. Например, [2, 5] обозначает интервал от 2 до 5 включительно. Если же числа не включаются, используются круглые и квадратные скобки вместе, например: (2, 5] — это полуоткрытый интервал от 2 до 5, не включая 2, но включая 5.

Таким образом, квадратные скобки играют важную роль в математике, позволяя структурировать и обозначать различные математические объекты и операции. Их применение включает в себя обозначение массивов, списков, множеств, элементов и интервалов. Понимание роли и значения квадратных скобок является неотъемлемой частью математической грамотности и облегчает работу с математическими выражениями.

Квадратные скобки в математике: определение и применение

В самом простом случае, квадратные скобки используются для обозначения массивов или векторов. Например, [1, 2, 3] может представлять массив из трех элементов или вектор с тремя компонентами.

Квадратные скобки также используются для обозначения интервалов. Например, [a, b] может обозначать закрытый интервал от a до b, который включает оба конца. В то же время, (a, b) обозначает полуоткрытый интервал, который включает только числа между a и b, но не самые a и b.

Кроме того, квадратные скобки могут использоваться для обозначения матриц. Например, [a b; c d] может представлять матрицу 2×2 с элементами a, b, c и d.

В некоторых математических областях, таких как теория множеств или теория вероятности, квадратные скобки могут иметь специальное значение и использоваться для обозначения событий, множеств или вероятностей.

Итак, квадратные скобки играют важную роль в математике и имеют различные применения в различных областях этой науки. Понимание и правильное использование этих символов является важным навыком для успешного изучения и применения математики.

Определение квадратных скобок

1. Векторы: квадратные скобки могут использоваться для обозначения векторов. Например, вектор a может быть записан как [a].

2. Матрицы: квадратные скобки также используются для обозначения матриц. Каждая строка матрицы обычно заключается в квадратные скобки, а элементы разделяются запятыми. Например, матрица A может быть записана следующим образом:

• [a11, a12, a13]
• [a21, a22, a23]
• [a31, a32, a33]

3. Индексы: квадратные скобки также используются для обозначения индексов. Например, a1 может быть записано как a[1].

4. Математические выражения: квадратные скобки могут использоваться для обозначения операций или выражений. Например, [x + y] обозначает сумму x и y, а [x * y] обозначает произведение x и y.

Все эти примеры демонстрируют различные способы использования квадратных скобок в математике. Их гибкость и универсальность делают их важным инструментом для обозначения и работы с различными математическими объектами.

Применение квадратных скобок в алгебре

Квадратные скобки в алгебре играют важную роль. Они используются для обозначения различных операций и свойств в алгебраических выражениях.

Одно из основных применений квадратных скобок в алгебре — обозначение матриц. Матрица представляет собой прямоугольную таблицу чисел или символов, расположенных в определенном порядке. Квадратные скобки используются для ограничения матрицы и отделения ее элементов друг от друга.

Кроме того, квадратные скобки используются для обозначения векторов. Вектор — это объект, характеризующийся направлением и длиной. В алгебре векторы могут быть записаны в виде столбца или строки чисел, разделенных квадратными скобками.

Также квадратные скобки используются для обозначения округления чисел. Если число округляется до ближайшего целого числа, то оно заключается в квадратные скобки.

В алгебре квадратные скобки могут также использоваться для указания приоритета операций. Если внутри квадратных скобок находится выражение, то оно должно быть выполнено первым.

В заключение, квадратные скобки широко применяются в алгебре для обозначения матриц, векторов, округления чисел и указания приоритета операций. Их использование помогает структурировать алгебраические выражения и упрощает их анализ и решение.

Применение квадратных скобок в теории вероятностей

В теории вероятностей квадратные скобки используются для обозначения вероятности события.

Пусть имеется некоторый случайный эксперимент, и пусть A — некоторое событие, связанное с этим экспериментом. Тогда вероятность события A обозначается как [A].

Квадратные скобки в данном контексте позволяют отличить вероятность от других математических обозначений, таких как функции и операции.

Применение квадратных скобок в теории вероятностей позволяет удобно и наглядно записывать вероятности различных событий и их комбинаций.

Например, если имеется два события A и B, то вероятность того, что произойдут оба этих события, может быть записана как [A и B]. Аналогично, вероятность того, что произойдет хотя бы одно из событий A или B, будет обозначаться как [A или B].

Также с помощью квадратных скобок можно записывать вероятности условных событий. Например, вероятность события A при условии, что произошло событие B, будет обозначаться как [A | B].

Применение квадратных скобок в теории вероятностей позволяет упростить и улучшить понимание вероятностных вычислений и сделать их более читабельными.

Применение квадратных скобок в физике

Квадратные скобки находят широкое применение в физике, особенно в области математического описания физических законов и формулирования уравнений.

Одним из основных применений квадратных скобок является обозначение векторов. В физике векторы используются для описания физических величин, которые имеют не только величину, но и направление. Квадратные скобки позволяют явно выделить векторы от других величин и обозначить их.

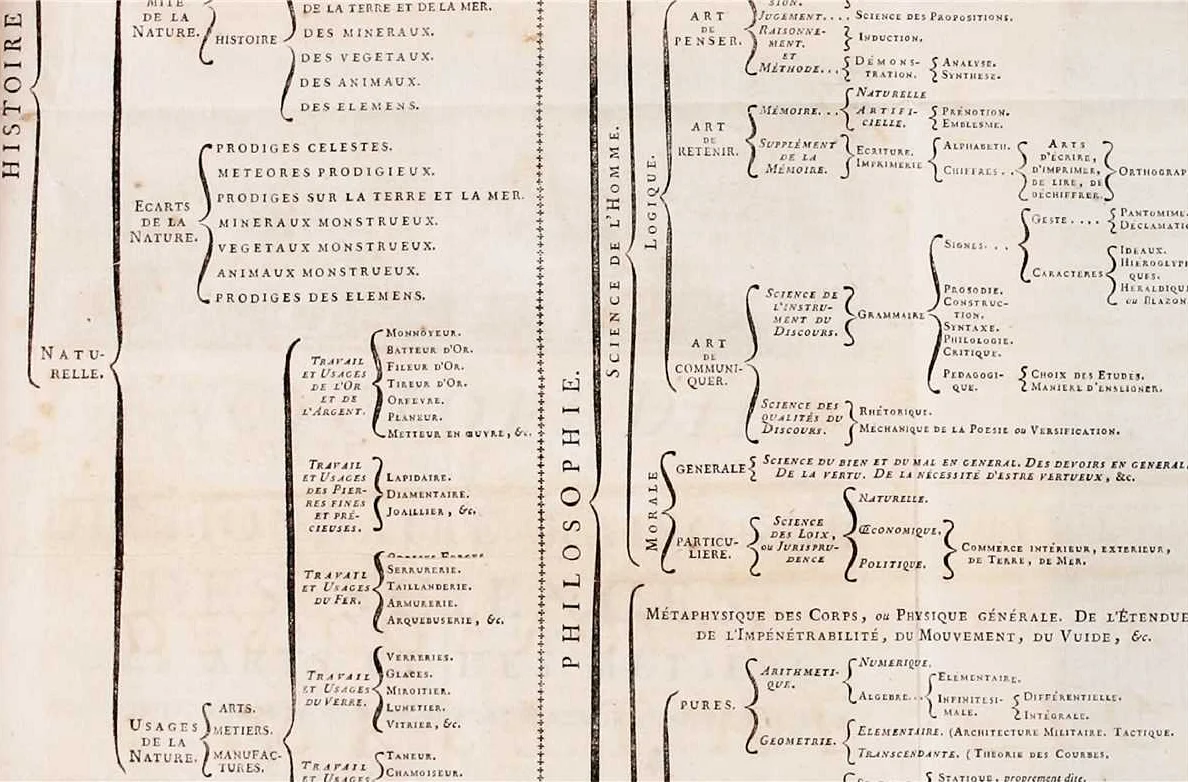
Кроме того, квадратные скобки используются для обозначения массивов или списков физических величин. Например, при описании движения тела в пространстве в физике используется вектор положения, который содержит координаты тела по каждому измерению. Координаты могут быть представлены в виде массива, где каждая координата сохраняется в отдельной ячейке массива, разделенной запятой.

Также квадратные скобки могут использоваться для обозначения матриц, которые являются важным инструментом в физике, особенно в теории поля и квантовой механике. Матрицы позволяют описывать различные физические величины и их взаимодействия в математическом виде. Квадратные скобки используются для выделения и обозначения отдельных элементов матрицы.

Применение квадратных скобок в программировании

Обращение к элементам массивов и списков происходит с помощью индексов. Индексация в привычной для нас форме с использованием квадратных скобок позволяет получить доступ к определенному элементу по его порядковому номеру.

Например, если у нас есть массив чисел [1, 2, 3, 4, 5], то чтобы получить доступ к элементу с индексом 2 (третий элемент), мы можем использовать следующую конструкцию: массив[2]. В результате получим значение 3.

Кроме того, квадратные скобки в программировании используются для создания и обращения к словарям. Словарь представляет собой структуру данных, которая хранит пары ключ-значение.

При создании словаря в квадратных скобках указывается ключ, за которым следует двоеточие и значение, например: {‘имя’: ‘Анна’, ‘возраст’: 25}. Для обращения к значению по ключу также используется квадратные скобки: словарь[‘имя’]. В результате получим значение ‘Анна’.

Таким образом, квадратные скобки в программировании позволяют удобно работать с массивами, списками и словарями, обращаться к их элементам и получать необходимую информацию.

Вопрос-ответ:

Зачем используются квадратные скобки в математике?

Квадратные скобки используются в математике для обозначения различных операций и объектов, таких как матрицы, векторы, индексы, и массивы.

Что обозначает использование квадратных скобок в матричных операциях?

В матричных операциях квадратные скобки используются для обозначения матрицы и указания ее элементов. Например, [1 2 3] обозначает матрицу с одной строкой и трех столбцов, а [1; 2; 3] обозначает матрицу с тремя строками и одним столбцом.

Какую роль играют квадратные скобки в векторах?

Векторы обычно записываются с использованием квадратных скобок, чтобы обозначить последовательность элементов. Например, [1 2 3] обозначает вектор с тремя элементами.

Как использование квадратных скобок связано с индексами?

В математике квадратные скобки используются для обозначения индексов элементов в массиве или последовательности. Например, A[1] обозначает первый элемент массива A.

Как квадратные скобки применяются в операциях с массивами?

В операциях с массивами квадратные скобки используются для указания индексов элементов или диапазонов элементов, которые нужно обработать. Например, A[1:5] обозначает подмассив, состоящий из элементов с индексами от 1 до 5 включительно.

Применение квадратных скобок в линейной алгебре

В линейной алгебре квадратные скобки широко используются для обозначения матриц и векторов.

Матрицы — это прямоугольные таблицы чисел, расположенных в виде строк и столбцов. Каждый элемент матрицы обозначается с помощью квадратных скобок, указывая номер строки и столбца, в котором он находится. Например, если матрица A имеет размерность 2×2, то ее элементы можно обозначить следующим образом:

[A11]	[A12]
[A21]	[A22]

Аналогично, векторы — это упорядоченные наборы чисел. Векторы могут быть представлены как столбцы или строки, и их компоненты также обозначаются с помощью квадратных скобок. Например, вектор x может быть представлен в виде столбца:

[x1]

[x2]

Квадратные скобки также используются для обозначения операций с матрицами и векторами. Например, для перемножения матриц A и B используется следующая формула:

[AB] = [A] * [B]

А для умножения матрицы A на вектор x используется формула:

[Ax] = [A] * [x]

Таким образом, квадратные скобки в линейной алгебре играют важную роль в обозначении и оперировании матрицами и векторами.

Видео по теме: