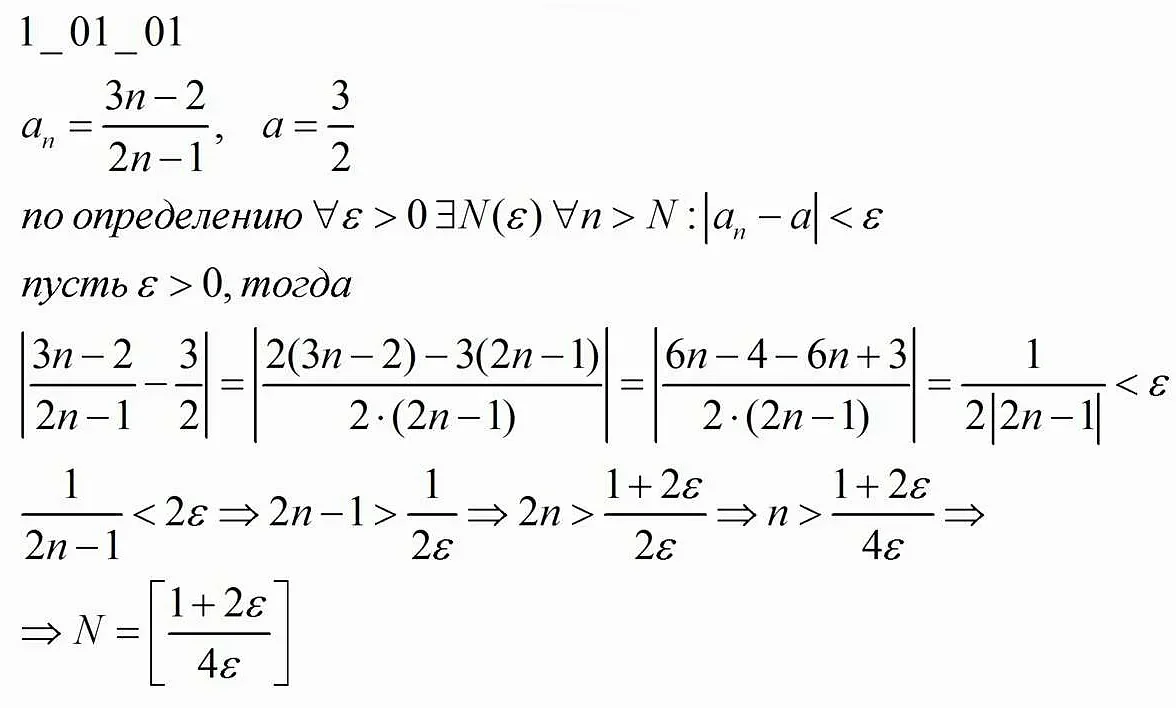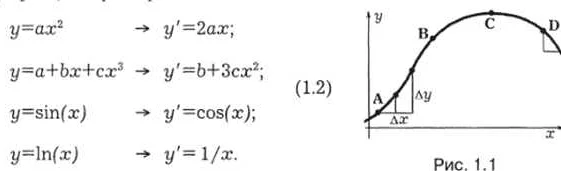С какого класса начинается высшая математика

Статья рассказывает о том, с какого класса в школе начинается изучение высшей математики. Узнайте, какие темы и задачи учатся на разных этапах обучения и какие навыки развиваются у учеников. Получите полное представление о том, какая математика изучается в начальной, средней и старшей школе.

Высшая математика – это дисциплина, которая является одной из важнейших в образовательной программе. Она знакомит студентов со сложными математическими концепциями и основами анализа. Однако, как часто это бывает, высшая математика начинается задолго до университета.

Уже в школе ученики начинают изучать основы этой науки. Обычно изучение высшей математики начинается с 7 класса. В этом возрасте дети уже достаточно подготовлены, чтобы понять и усвоить базовые математические концепции.

Обычно программа школьного курса включает изучение алгебры, геометрии, математического анализа и теории вероятности. Начиная с младших классов, дети изучают основы алгебры и геометрии, а затем, постепенно, расширяют свои знания и навыки в этих областях.

Изучение высшей математики в школе имеет множество преимуществ. Во-первых, это помогает ученикам развивать абстрактное мышление, логическое мышление и проблемное мышление. Во-вторых, это создает прочную основу для дальнейшего изучения математики в университете.

Что такое высшая математика и с чего начинается ее изучение в школе?

В школьной программе высшая математика начинается изучаться с 10 класса. В этом классе ученики начинают знакомиться с основными понятиями и методами высшей математики, такими как функции, производные, интегралы и дифференциальные уравнения. На этом этапе ученики получают базовые знания и навыки, которые позволяют им понять и применять основные принципы высшей математики.

Основы математики: первый шаг в высшую математику

Основы математики изучаются в школе и являются первым шагом в познании мира математики. Обычно начинают изучение основ математики с первого класса. В начальной школе дети изучают основы арифметики, геометрии и алгебры. Они учатся считать, складывать и умножать числа, находить площади и объемы геометрических фигур, решать простые уравнения и задачи.

Во втором и третьем классах изучение основ математики продолжается. Дети углубляют свои знания в арифметике, учатся делить числа с остатком, решать задачи на доли. Они также знакомятся с основами геометрии, изучают понятия о прямых, углах, треугольниках и прямоугольниках.

В четвертом классе дети начинают изучать алгебру. Они знакомятся с понятиями об уравнениях и переменных, учатся решать простые уравнения с одной переменной. Также в этом классе дети начинают изучать таблицу умножения и углубляют свои знания в геометрии.

Вплоть до конца школьной программы, дети продолжают изучать основы математики и углублять свои знания в различных областях этой науки. В результате этого изучения, они получают хорошую математическую подготовку и становятся готовыми для изучения высшей математики в университете.

Алгебра: второй этап в изучении высшей математики

Алгебра занимается изучением абстрактных символов и операций над ними. Учащиеся изучают такие понятия, как переменная, коэффициент, степень, многочлен и уравнение. Они также изучают различные операции над многочленами, такие как сложение, вычитание, умножение и деление.

В изучении алгебры также важно понимание графиков функций и решение уравнений и неравенств. Учащиеся учатся анализировать и интерпретировать графики функций, а также находить их основные характеристики, такие как экстремумы и асимптоты.

Алгебра является основой для многих других разделов математики, таких как геометрия, тригонометрия и математический анализ. Поэтому важно усвоение алгебры на этом этапе в изучении математики, чтобы успешно продолжать обучение в этих разделах.

В школьной программе алгебра обычно изучается начиная с 7-8 класса и продолжается на протяжении нескольких лет. Ученики изучают различные темы алгебры, такие как многочлены, уравнения и неравенства, системы уравнений, функции и графики, матрицы и дроби.

Изучение алгебры на этом этапе помогает развить логическое мышление и абстрактное мышление учащихся. Оно также помогает ученикам развить навыки решения проблем и критического мышления, которые могут быть полезными во многих других областях жизни.

Геометрия: важная составляющая высшей математики

В начальной школе ученики изучают понятия пространства, фигур и их свойства. Они учатся сравнивать длины, углы и площади, решать простые задачи на конструирование и измерение. Знакомство с геометрией продолжается и в старших классах, где ученики изучают более сложные концепции и методы решения задач.

В высшей математике геометрия играет важную роль в различных областях. Она используется в алгебре, математическом анализе, дифференциальной геометрии и других дисциплинах. Геометрический подход позволяет лучше понять и описать сложные математические объекты и отношения между ними.

Важно отметить, что геометрия также имеет практическое применение в различных областях науки и техники. Она помогает в решении задач физики, инженерии, компьютерной графики и других областей. Знание геометрии позволяет анализировать и моделировать сложные системы и их поведение.

Таким образом, геометрия является важной составляющей высшей математики и имеет широкое применение в науке и технике. Понимание геометрических концепций и методов позволяет более глубоко понять и использовать математику в различных областях знания.

Математический анализ: основы и принципы

Основы математического анализа начинают изучать в средней школе, в 8-9 классе. Ученики знакомятся с понятием функции, изучают арифметические и геометрические прогрессии, осваивают основы теории вероятностей.

В старших классах программу изучения математического анализа расширяют и углубляют. Учащиеся изучают понятие предела функции, производную и интеграл. Они учатся применять эти знания для решения различных математических задач, а также для анализа функций и их графиков.

Принципы математического анализа лежат в основе многих других научных и инженерных дисциплин. Они позволяют проводить точные исследования, находить оптимальные решения и делать предсказания на основе математических моделей.

Основы математического анализа, полученные в школьной программе, становятся прочной базой для дальнейшего изучения этой дисциплины на уровне вуза и для применения ее в реальных практических задачах.

Тригонометрия: ключевой раздел высшей математики

В начальных классах школы, основные понятия тригонометрии вводятся через изучение прямоугольных треугольников. Ученики узнают о соотношениях между длинами сторон треугольника и значениями тригонометрических функций, таких как синус, косинус и тангенс.

В более продвинутых классах, изучение тригонометрии становится более абстрактным. Ученики узнают о тригонометрических функциях, их графиках и свойствах. Они изучают периодические функции, тригонометрические тождества и формулы, а также применение тригонометрии в геометрии и физике.

Тригонометрия имеет широкое применение в различных областях, включая физику, инженерию, астрономию и информатику. Понимание основных принципов и концепций тригонометрии играет важную роль в развитии математического мышления и подготовке учеников к дальнейшему изучению математики и ее применению в реальных ситуациях.

Тригонометрические функцииОпределениеСвойства

Синус (sin)	Отношение противоположной стороны к гипотенузе	Периодичность, максимальное и минимальное значение, ординарные и особые точки
Косинус (cos)	Отношение прилежащей стороны к гипотенузе	Периодичность, максимальное и минимальное значение, ординарные и особые точки
Тангенс (tg)	Отношение синуса к косинусу	Периодичность, максимальное и минимальное значение, ординарные и особые точки

Векторная алгебра и аналитическая геометрия

Векторная алгебра занимается исследованием векторов и операций над ними. Вектор представляет собой математический объект, который имеет как величину, так и направление. Векторы используются для описания различных физических величин, таких как сила, скорость, ускорение и т.д. Векторная алгебра включает в себя операции сложения, вычитания, умножения на число и скалярное умножение векторов.

Аналитическая геометрия связывает геометрические фигуры с координатами. Этот раздел математики изучает методы решения геометрических задач с использованием алгебраических методов. Основной инструмент аналитической геометрии — это система координат, в которой каждая точка в пространстве имеет свои координаты.

Векторная алгебра и аналитическая геометрия часто используются в других областях науки, таких как физика, механика, информатика и др. Поэтому эти разделы математики являются важным кирпичиком в формировании базовых знаний и навыков учеников.

Изучение векторной алгебры и аналитической геометрии помогает ученикам развивать логическое мышление, абстрактное мышление, аналитические и пространственные навыки. Эти разделы также помогают ученикам лучше понимать и анализировать разнообразные задачи и ситуации, связанные с физическими явлениями и геометрическими фигурами.

Примеры тем векторной алгебры и аналитической геометрии:

Сложение и вычитание векторов

Умножение вектора на число

Скалярное умножение векторов

Понятие линейной зависимости и независимости векторов

Проекция вектора на ось

Уравнение прямой в пространстве

Уравнение плоскости в пространстве

Дифференциальные уравнения: сложный, но увлекательный раздел

Дифференциальные уравнения широко применяются в различных науках, таких как физика, экономика, биология и многих других. Они позволяют моделировать и анализировать различные процессы и явления, которые описываются через производные.

Решение дифференциальных уравнений требует глубокого понимания математических понятий и методов. Для этого необходимо обладать знаниями алгебры, аналитической геометрии и математического анализа.

Однако, несмотря на сложность, изучение дифференциальных уравнений может быть увлекательным и интересным. Оно позволяет увидеть связь между различными математическими понятиями и применить их для решения реальных проблем.

Дифференциальные уравнения делятся на разные типы в зависимости от своих характеристик и методов их решения. Среди них: обыкновенные дифференциальные уравнения, частные дифференциальные уравнения, линейные и нелинейные уравнения и многие другие.

Изучение дифференциальных уравнений начинается в высшей математике, обычно на 10-11 классе. Первоначально изучаются простые уравнения первого порядка, а затем переходят к более сложным и общим случаям.

Овладение дифференциальными уравнениями открывает двери в мир математического моделирования и анализа. Этот раздел математики помогает понять и описать законы природы и явления, которые нас окружают. В дальнейшем, эти знания могут быть применены в различных областях науки и техники.

Теория вероятностей: заключительный этап изучения высшей математики в школе

Основная цель изучения теории вероятностей заключается в том, чтобы помочь ученикам понять и применять основные понятия и методы этой науки. Она включает в себя изучение вероятности, случайности, статистики и других математических инструментов, которые позволяют анализировать и прогнозировать различные случайные явления.

В рамках изучения теории вероятностей ученики узнают о вероятностных моделях, вероятностных пространствах, случайных величинах, законах распределения и многом другом. Они также изучают методы статистического анализа данных и применение математических моделей для решения реальных задач.

Изучение теории вероятностей позволяет ученикам развить критическое мышление, аналитические навыки и умение работать с большими объемами данных. Это дисциплина, которая находит применение в различных областях, таких как экономика, физика, биология, компьютерные науки и другие.

Теория вероятностей является важным элементом общего математического образования и подготовки школьников к высшему образованию. Она помогает ученикам развить логическое мышление, решать сложные задачи и анализировать данные. Знание теории вероятностей также полезно в повседневной жизни, помогая принимать взвешенные решения на основе данных и статистики.

Таким образом, теория вероятностей является заключительным этапом изучения высшей математики в школе. Она предоставляет ученикам необходимые знания и навыки для работы с вероятностными моделями и анализа данных, а также развивает их математическое мышление и аналитические способности.

Вопрос-ответ:

Какие классы включены в школьную программу по высшей математике?

В школьной программе по высшей математике включены классы с 10 по 11. В 10 классе изучаются основы математического анализа, алгебры и геометрии, а в 11 классе углубленно изучаются данные разделы математики.

С каких тем начинается изучение высшей математики в школе?

Изучение высшей математики в школе начинается с основных понятий математического анализа и алгебры. В 10 классе учатся решать уравнения, неравенства, работать с функциями, а в 11 классе изучаются производные и интегралы, матрицы и системы уравнений.

Какие навыки и знания можно получить, изучая высшую математику в школе?

Изучение высшей математики в школе позволяет получить навыки решения сложных математических задач, анализировать и обрабатывать данные, развивать логическое мышление и абстрактное мышление. Также изучение высшей математики помогает усвоить основы математического анализа, алгебры и геометрии, что может пригодиться в дальнейшем образовании и профессиональной деятельности.

Какой уровень сложности имеют задачи по высшей математике в школе?

Задачи по высшей математике в школе имеют разный уровень сложности. В 10 классе они начинаются с простых уравнений и неравенств, но с каждым классом задания становятся сложнее. В 11 классе ученики решают задачи с производными и интегралами, матрицами и системами уравнений, что требует более глубокого понимания математических понятий и навыков решения задач.

Почему изучение высшей математики в школе важно для дальнейшего образования и карьеры?

Изучение высшей математики в школе важно для дальнейшего образования и карьеры, потому что оно помогает развить логическое мышление, абстрактное мышление и аналитические способности, которые необходимы во многих областях знаний и профессий. Также высшая математика является основой для изучения более сложных математических дисциплин в высшем образовании, таких как математический анализ, алгебра, дифференциальные уравнения и другие.

С какого класса начинается изучение высшей математики?

Изучение высшей математики начинается с университетского уровня образования. В школе в первую очередь изучаются основы математики, а высшая математика — это уже более сложный и глубокий уровень математических знаний, который изучается в специальных математических классах в университете.

Видео по теме: