Седло как математическая поверхность

Седло — это математическая поверхность, которая имеет форму изгибающегося вверх или вниз параболоида. Поверхность седла характеризуется наличием двух осей симметрии и точки седлообразного перегиба, где кривизна меняет знак. Изучение седел как математических объектов является важной частью аналитической геометрии и дифференциальной геометрии.

Седло – одна из самых интересных математических поверхностей, которая имеет множество особенностей и находит широкое применение в различных областях науки и техники. Она представляет собой поверхность, которая симметрична относительно двух перпендикулярных осям, и имеет форму, напоминающую седло.

Особенностью седла является то, что в каждой точке поверхности существует и только одна кривизна, а направление кривизны может меняться. Это приводит к тому, что седло может иметь необычные геометрические свойства, такие как наличие максимума или минимума, а также точек перегиба.

Седло находит применение во многих областях науки и техники. Например, оно используется в геометрии для изучения свойств кривых и многогранников. Также седло является неотъемлемой частью теории устойчивости и контроля систем, где оно используется для анализа устойчивости различных процессов и управления ими.

Необычная форма седла позволяет создавать уникальные конструкции и обеспечивать нестандартные свойства объектов. Она находит применение в архитектуре, дизайне и инженерии, способствуя созданию инновационных решений и развитию новых технологий.

Таким образом, седло как математическая поверхность обладает уникальными особенностями и находит широкое применение в различных областях науки и техники. Его форма и свойства позволяют создавать нестандартные конструкции и обеспечивать инновационные решения. Изучение седла имеет большое значение для развития современных научных и технических дисциплин.

Что такое седло: математическая поверхность

Седло представляет собой поверхность, которая выглядит как седло на коне. Одна из особенностей седла — это наличие двух направлений, вдоль которых поверхность выпуклая, а вдоль других двух направлений — вогнутая.

Математические седла могут быть описаны с помощью уравнений, которые определяют их форму и геометрические свойства. Седло является особенным типом поверхности, так как оно не является ни положительно, ни отрицательно кривизны.

Седла широко используются в математике и физике для моделирования и анализа различных явлений. Например, они могут быть использованы для изучения динамики систем, определения точек экстремума функций и решения уравнений.

В основе использования седел лежит их способность обладать различными свойствами в разных направлениях, что делает их полезными инструментами в науке и инженерии.

Вывод: седло — это математическая поверхность с особыми формой и свойствами, которая находит широкое применение в различных областях науки и техники.

Определение и особенности седла

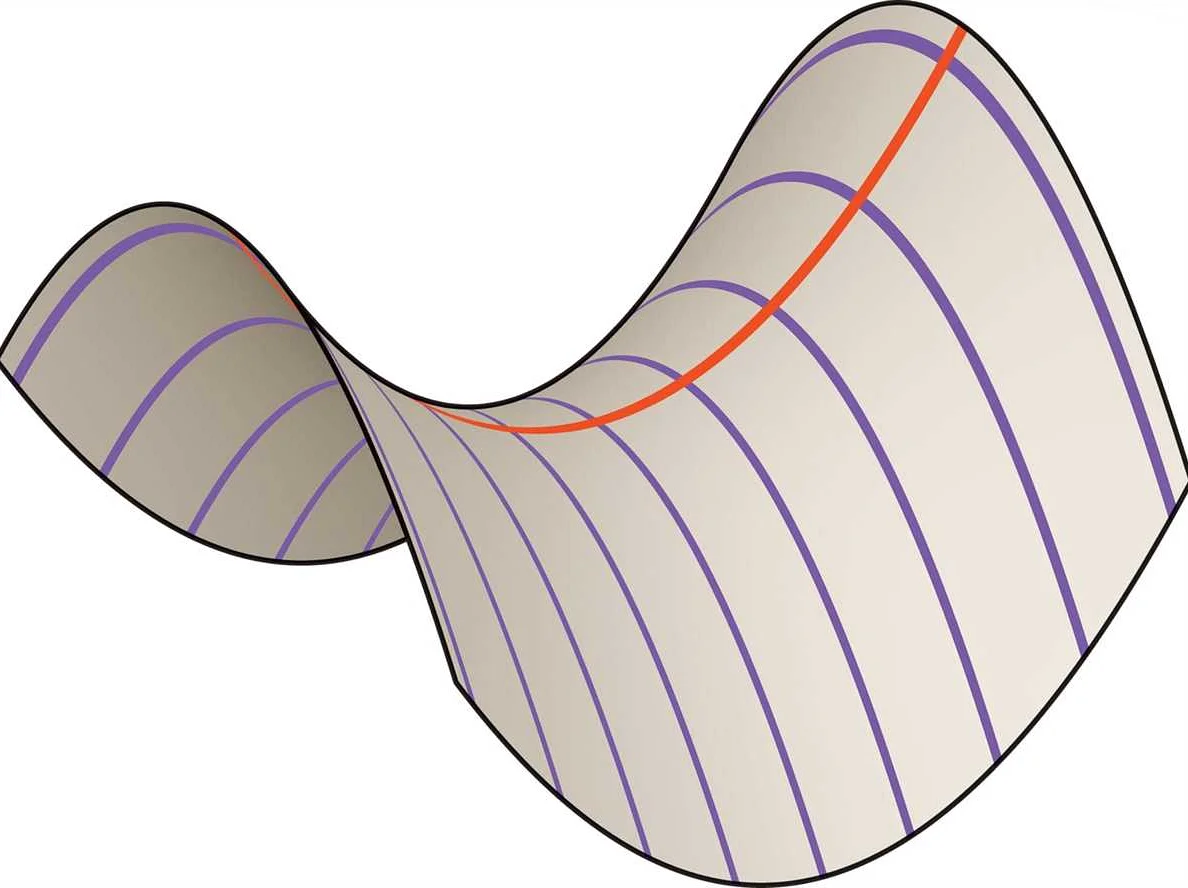
Особенностью седла является то, что она имеет два главных направления. Вдоль одного из них поверхность выпукла, а вдоль другого — вогнута. Это означает, что в седле существуют участки, где кривизна положительна, и участки, где кривизна отрицательна.

Седло часто используется в математических моделях и приложениях, таких как теория оптимизации, анализ функций и геометрия. Оно применяется для изучения кривизны, точек экстремума и других свойств функций и поверхностей.

Седло также является примером поверхности с отрицательной кривизной, которая имеет значение в физике и инженерии. Например, в аэродинамике седло используется для изучения потоков воздуха вокруг крыла самолета, чтобы определить его аэродинамические характеристики.

Геометрические свойства седла

1. Точка перегиба: седло является поверхностью, у которой существует точка перегиба. Эта точка является особенной, так как она является местом, где кривизна поверхности изменяется с положительной на отрицательную или наоборот.

2. Принципальные кривизны: седло имеет две принципальные кривизны, которые определяют ее форму. Одна из кривизн положительна, а другая — отрицательна. Это делает седло уникальной поверхностью с нетривиальной геометрией.

3. Плоскости касательных: на каждой точке седла существуют две плоскости касательных, которые перпендикулярны друг другу и пересекаются в этой точке. Эти плоскости играют важную роль в изучении свойств седла и его окружающего пространства.

4. Форма и тип: седло может иметь различные формы и типы, в зависимости от его параметров и уравнений. Оно может быть острым или плоским, симметричным или асимметричным. Это делает седло интересной объектом исследования для математиков и геометров.

Все эти геометрические свойства седла делают его важным объектом исследования в различных областях науки и техники. Оно находит применение в анализе функций, визуализации данных, конструировании и многих других областях.

Математические модели седла

Математические модели седла могут быть представлены различными способами. Одним из наиболее распространенных способов является использование уравнений поверхности. Уравнения могут быть заданы в виде аналитических формул или в виде параметрических уравнений.

Аналитическое задание седла позволяет определить ее геометрические свойства и сделать выводы о ее характеристиках. Параметрическое задание седла позволяет получить набор параметров, которые могут быть использованы для построения графика поверхности.

Седло является одной из самых простых и удобных моделей для исследования различных математических свойств. Она имеет много применений в различных областях науки и техники, включая математику, физику, экономику и инженерию.

Математические модели седла играют важную роль в понимании и анализе сложных систем и процессов. Они позволяют исследовать различные аспекты поведения системы, такие как устойчивость, сходимость и оптимальность.

Использование математических моделей седла позволяет решать различные задачи, включая оптимизацию, прогнозирование и управление. Это помогает лучше понять и предсказать поведение реальных систем и принять решения на основе полученных результатов.

Функциональное применение седел в математике

Седловые точки функции – это точки, в которых градиент функции равен нулю и направление изменения функции меняется с выпуклого на вогнутое или наоборот. Такие точки являются ключевыми для определения экстремумов функции.

Седловые точки функций могут быть найдены с использованием различных методов математического анализа, таких как методы дифференциального исчисления, методы оптимизации и другие.

Одно из основных применений седел в математике – это оптимизация функций. Оптимизация – это процесс нахождения экстремальных точек функции в заданном диапазоне значений аргумента. Седла позволяют оптимизировать функции, находя экстремальные точки и определяя их характеристики, такие как минимумы, максимумы или седловые точки.

Кроме того, седла широко применяются в теории игр, где используются концепции седловой точки и седлового равновесия. Седловая точка в теории игр – это точка, в которой стратегия одного игрока является оптимальной при выборе стратегии другого игрока. Это концепция, которая позволяет определить оптимальную стратегию игры и предсказать исход игры.

Таким образом, седла, как математическая поверхность, имеют важное функциональное применение в различных областях математики, таких как анализ функций, оптимизация и теория игр. Изучение седел и их свойств позволяет получить глубокое понимание математических моделей и применять их для решения различных задач.

Применение седла в физике и инженерии

Одним из применений седла является изучение динамики систем. С помощью седловой точки, которая является особым типом точки на седле, можно определить устойчивость и неустойчивость системы. Это особенно важно в физике, где системы могут иметь сложную динамику и различные степени стабильности.

Еще одним применением седла в физике является моделирование и анализ электромагнитных полей. С помощью седловых поверхностей можно представить распределение электрического или магнитного поля и исследовать его свойства. Это широко применяется в инженерии при проектировании и оптимизации электромагнитных систем.

Также седло находит применение в инженерии при решении задач механики и конструкционного проектирования. С помощью седловых поверхностей можно определить напряжения и деформации в конструкциях и предсказать их поведение в различных условиях нагрузки. Это позволяет создавать более надежные и эффективные конструкции.

В заключение, седло как математическая поверхность находит широкое применение в физике и инженерии. Его особенности позволяют решать различные задачи, связанные с динамикой систем, электромагнитными полями и конструкционным проектированием.

Применение седел в компьютерной графике и дизайне

Седло, как математическая поверхность, находит широкое применение в компьютерной графике и дизайне. Его уникальная форма и особенности позволяют создавать интересные и оригинальные визуальные эффекты.

В компьютерной графике седло может быть использовано для создания трехмерной модели объекта. Оно позволяет добавить реалистичность и глубину изображению, делая его более привлекательным и узнаваемым.

Седло также может быть использовано для создания эффекта освещения. Благодаря своей форме, седло может отражать свет по-разному, создавая интересные игры теней и переходов света. Это позволяет придать изображению объем и динамичность.

Кроме того, седло может быть использовано в дизайне для создания уникальных и запоминающихся логотипов или графических элементов. Его форма может символизировать движение, взлет или волнение, что делает его особенно привлекательным для использования в различных проектах.

Использование седел в компьютерной графике и дизайне позволяет создавать уникальные и оригинальные визуальные эффекты, делая изображения более привлекательными и запоминающимися. Благодаря своей форме и особенностям, седло является важным инструментом для дизайнеров и графических художников.

Применение седел в архитектуре и декоре

Седло, как математическая поверхность, нашло свое применение в архитектуре и декоре. Ее уникальные геометрические свойства и привлекательный внешний вид делают ее популярным элементом в различных объектах и конструкциях.

В архитектуре седло может быть использовано для создания оригинальной формы крыши здания. Его изгибы и линии могут придать зданию уникальный и современный вид. Такая форма крыши также может быть функциональной, позволяя собирать дождевую воду и использовать ее для полива или других нужд.

Седло также может быть использовано в декоре интерьера. Его изящные линии и формы могут стать украшением стен, потолка или мебели. С использованием седла можно создать интересные композиции, добавить оригинальность и стиль в пространство.

Кроме того, седло может быть использовано в ландшафтном дизайне. Его форма может послужить основой для создания оригинальных садовых конструкций, фонтанов или пейзажных элементов. Седло может добавить гармонии и эстетической привлекательности в окружающую среду.

В заключение, седло, как математическая поверхность, находит широкое применение в архитектуре и декоре. Его уникальные геометрические свойства и красивый внешний вид делают его популярным элементом в различных объектах и конструкциях, придавая им оригинальность и стиль.

Вопрос-ответ:

Как можно описать математическую структуру седловой поверхности?

Седловая поверхность — это математическая поверхность, которая выглядит как седло, то есть имеет две противоположные выпуклости вдоль одной оси и две противоположные вогнутости вдоль другой оси.

Как можно создать седловую поверхность?

Создать седловую поверхность можно с помощью математических функций, задающих координаты каждой точки на поверхности. Например, функция z = x^2 — y^2 создаст седловую поверхность.

В каких областях науки и техники применяются седловые поверхности?

Седловые поверхности широко применяются в различных областях науки и техники. Например, они используются в математике для изучения нелинейных уравнений, в физике для моделирования поверхности потенциала, а также в инженерии и дизайне для создания оптимальных форм и структур.

Какие свойства имеют седловые поверхности?

Седловые поверхности обладают несколькими особыми свойствами. Они имеют два главных кривизны, одна из которых положительная, а другая отрицательная. Кроме того, седловые поверхности являются неоднородными по кривизне и не имеют оси симметрии.

Какие примеры седловых поверхностей можно привести?

Несколько примеров седловых поверхностей включают параболический гиперболоид, гиперболическую параболоиду и поверхность Римана с отрицательной кривизной. Все эти поверхности имеют характеристическую форму седла.

Каково определение математической поверхности?

Математическая поверхность — это абстрактный объект, который может быть представлен в виде двумерной поверхности в трехмерном пространстве. Она может быть описана уравнением или параметрическими уравнениями.

Видео по теме: