Что такое схема в математике 5 класс

Схема в математике для учеников 5 класса представляет собой графическое изображение, которое позволяет визуально представить и структурировать информацию. С помощью схемы можно легко организовать и запомнить математические понятия и формулы, улучшить понимание и запоминание учебного материала.

Схема в математике – это наглядная графическая модель, которая помогает систематизировать, упорядочить и анализировать информацию. Она является основным инструментом для решения задач и обобщения математических знаний. В пятом классе схемы используются для изучения различных математических понятий, включая геометрию, алгебру, статистику и другие области.

Схемы в математике могут быть разных типов: схемы классификации, схемы последовательностей, схемы причинно-следственных связей и т.д. Они помогают ученикам увидеть связи между различными элементами и понять их взаимоотношения. Например, при изучении геометрии схема может помочь организовать информацию о разных фигурах, их свойствах и классификации.

Пример: При изучении понятия «параллельные прямые» учитель может использовать схему, на которой изображены две параллельные прямые и их взаимное расположение относительно других прямых. Эта схема позволяет ученикам визуально представить, что значит быть параллельными и как это связано с углами и другими геометрическими понятиями.

Схемы в математике помогают развивать логическое мышление, аналитические и абстрактные способности учеников. Они также помогают учащимся организовывать информацию и улучшать понимание математических концепций. Поэтому, использование схем – важный элемент обучения математике в пятом классе и дальше.

Схема в математике 5 класс

В пятом классе схемы широко используются для решения задач, составления алгоритмов и представления математических моделей.

Примером использования схемы в математике может служить задача о нахождении площади прямоугольника. Схема решения данной задачи может выглядеть следующим образом:

1. Вводим значения сторон прямоугольника.
2. Умножаем значение одной стороны на значение другой стороны.
3. Полученный результат является площадью прямоугольника.

Такая схема позволяет систематизировать и упорядочить последовательность действий, необходимых для решения задачи, и обеспечивает понятность и наглядность.

Схемы могут быть представлены в виде блок-схем, диаграмм, таблиц и других графических элементов. Они помогают ученикам более точно понимать математические концепции, развивают логическое мышление и умение анализировать информацию.

Определение и назначение схемы

Назначение схемы заключается в том, чтобы сделать математическую задачу более понятной и удобной для решения. Она помогает структурировать информацию и предоставляет визуальные подсказки для решения задачи.

В схеме часто используются различные геометрические фигуры, стрелки, символы и текстовые описания. Они позволяют наглядно представить связи между элементами, операции и последовательность действий.

Схемы широко применяются в математике для решения задач, построения графиков, анализа данных и представления математических концепций. Они помогают ученикам лучше понять и запомнить материал, а также развивают логическое мышление и умение анализировать информацию.

Примеры схемы в математике 5 класс

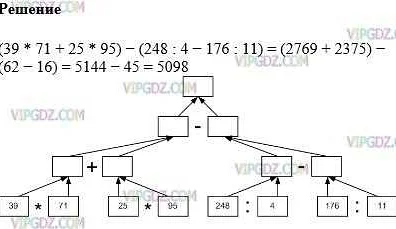
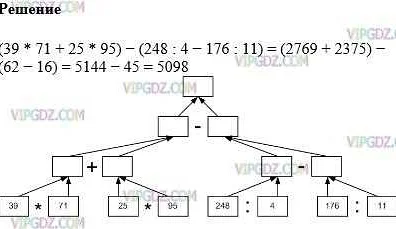
В 5 классе ученикам предлагаются различные примеры схем, которые помогают структурировать информацию и решать задачи более эффективно. Вот несколько примеров схем, которые изучаются в 5 классе:

Схема «Дерево решений» – используется для поиска решений задачи путем последовательного выбора вариантов. Вершины дерева соответствуют возможным вариантам выбора, а листья – решениям задачи.

Схема «Таблица истинности» – используется для анализа логических выражений. В таблице истинности отображаются все возможные значения переменных и результаты вычисления выражения.

Схема «Стрелки и блоки» – используется для представления последовательности действий или алгоритма. Блоки представляют отдельные действия, а стрелки указывают на последовательность выполнения этих действий.

Все эти схемы помогают ученикам более ясно представить информацию и решать задачи, используя логическое мышление и систематический подход. Они также развивают навыки работы с графическими представлениями и анализа информации.

Схема решения уравнений

1. Перенос всех слагаемых, содержащих неизвестные, в одну сторону уравнения, а все числа в другую сторону.

2. Сокращение подобных слагаемых.

3. Перенос всех слагаемых с неизвестными в одну сторону и все числа в другую сторону.

4. Разделение обеих сторон уравнения на коэффициент неизвестной.

5. Подстановка полученного значения неизвестной в исходное уравнение и проверка корректности решения.

Например, рассмотрим уравнение 2x + 5 = 15. Применяя схему решения, мы можем перенести слагаемое 5 в другую сторону, получив 2x = 15 — 5, что эквивалентно 2x = 10. Затем мы разделим обе стороны на коэффициент неизвестной, получив x = 10 / 2, что равно x = 5. Подставляя это значение в исходное уравнение, мы получаем 2 * 5 + 5 = 15, что верно.

Схема решения уравнений является важным инструментом в математике, который помогает учащимся развивать логическое мышление и навыки решения задач.

Схема решения задач на пропорциональность

Для решения задач на пропорциональность можно использовать следующую схему:

Шаг 1: Сначала выписываем условие задачи и указываем данные, которые нам даны.

Шаг 2: Далее находим коэффициент пропорциональности (к) путем деления одной из величин на другую.

Шаг 3: После нахождения коэффициента пропорциональности (к) составляем пропорцию, подставляя известные значения величин.

Шаг 4: Решаем полученную пропорцию, находя неизвестное значение.

Шаг 5: Проверяем полученный результат путем подстановки найденного значения в исходное условие задачи.

Пример: Если 5 килограммов яблок стоят 200 рублей, то сколько будут стоить 3 килограмма яблок?

Шаг 1: Условие задачи: 5 кг яблок стоят 200 рублей, найти стоимость 3 кг яблок.

Шаг 2: Коэффициент пропорциональности (к) равен 200 рублей / 5 кг = 40 рублей/кг.

Шаг 3: Составляем пропорцию: 5 кг / 200 рублей = 3 кг / х рублей.

Шаг 4: Решаем пропорцию: 5 кг * х рублей = 3 кг * 200 рублей.

Шаг 5: Проверяем результат: 5 кг * 40 рублей = 200 рублей, что соответствует условию задачи.

Таким образом, стоимость 3 кг яблок составляет 120 рублей.

Схема решения задач на доли

Решение задач на доли в математике можно разбить на несколько шагов. Вот основная схема решения таких задач:

1. Определить общую единицу измерения, к которой будут приводиться доли. Например, если речь идет о долях от целого числа, то общей единицей измерения может быть само это число.
2. Привести все доли к общей единице измерения. Для этого нужно выполнить соответствующие преобразования. Например, если имеются доли 1/4 и 1/2, то можно привести их к общей единице, умножив первую долю на 2 и вторую на 4.
3. Выполнить необходимые действия с приведенными долями. Например, если нужно сложить доли, то сложить числители и сохранить общий знаменатель.
4. Если требуется, выразить ответ в виде десятичной дроби или процента. Для этого нужно произвести соответствующие вычисления.

Применение этой схемы позволяет систематизировать процесс решения задач на доли и избежать ошибок. Решая задачи по такой схеме, ученики могут более уверенно и точно выполнять математические операции с долями.

Схема решения задач на проценты

Решение задач на проценты включает в себя несколько шагов:

1. Определение известных данных. Вначале необходимо четко понять, какие данные даны в задаче и что именно нужно найти.
2. Определение неизвестных данных. Если в задаче даны данные о процентах, нужно выяснить, какие именно значения нужно найти.
3. Выражение условия задачи в виде уравнения. На этом шаге необходимо перевести условие задачи в язык математических операций. Это поможет сформулировать уравнение, которое будет использоваться для решения задачи.
4. Решение уравнения. После того, как уравнение составлено, необходимо его решить, чтобы найти значение неизвестной величины.
5. Проверка полученного результата. Важно всегда проверять корректность полученного ответа путем подстановки его в исходное уравнение или условие задачи. Если ответ верный, задача считается решенной.

Приведем пример задачи, чтобы лучше понять схему решения задач на проценты:

Задача: Цена товара составляет 8000 рублей. Через год она увеличится на 12%. Какая будет новая цена товара?

1. Известные данные: исходная цена товара — 8000 рублей, процент увеличения — 12%.
2. Неизвестные данные: новая цена товара.
3. Уравнение: исходная цена + исходная цена * процент увеличения = новая цена товара. В данном случае это 8000 + 8000 * 0.12 = новая цена товара.
4. Решение: 8000 + 8000 * 0.12 = 8000 + 960 = 8960 рублей. Таким образом, новая цена товара будет составлять 8960 рублей.
5. Проверка: 8000 + 8000 * 0.12 = 8960 рублей. Полученный результат соответствует условию задачи, следовательно, ответ верный.

Теперь, зная схему решения задач на проценты, вы сможете успешно решать подобные задачи и получать правильные ответы.

Схема решения задач на площадь и периметр

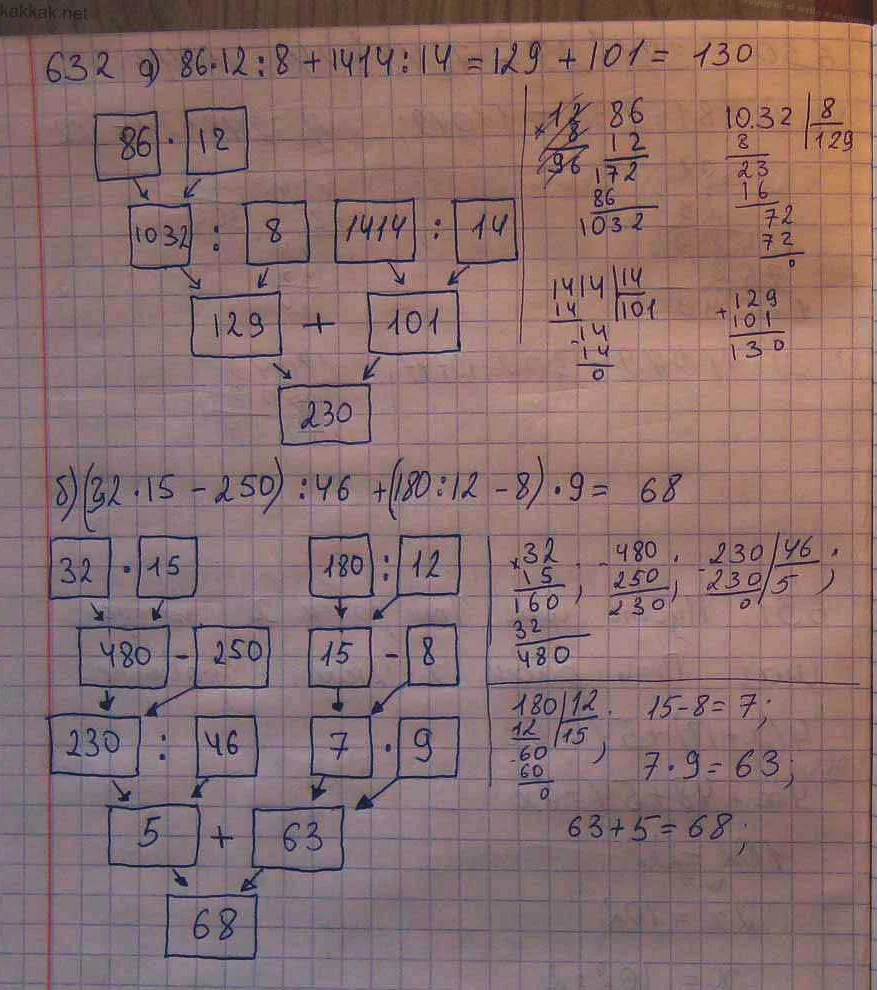
Решение задач на площадь и периметр требует определения данных величин и использования соответствующих формул. Для успешного решения задачи следуйте следующей схеме:

1. Прочитайте условие задачи и определите, что именно требуется найти: площадь или периметр.
2. Если в условии задачи даны все необходимые данные, перейдите к следующему шагу. В противном случае, определите, какие данные необходимо найти.
3. Изучите данные и используйте соответствующие формулы для нахождения площади и периметра.
4. Выполните необходимые вычисления, используя формулы и данные из условия задачи.
5. Проверьте правильность полученных результатов и ответьте на поставленный вопрос задачи.

Пример решения задачи на площадь и периметр:

Условие задачи:Решение:

Найти площадь прямоугольника, если его стороны равны 5 см и 8 см.

Для нахождения площади прямоугольника используется формула: Площадь = длина * ширина В данном случае: Длина = 5 см Ширина = 8 см Подставляем значения в формулу: Площадь = 5 см * 8 см = 40 см² Ответ: Площадь прямоугольника равна 40 см².

Используя данную схему решения, вы сможете успешно решать задачи на площадь и периметр.

Схема решения задач на объем и массу

Решение задач на объем и массу включает в себя следующую схему:

1. Определите известные данные. В задаче указывается какие-то известные значения, например, объем или масса одного из веществ. Запишите эти значения.
2. Определите неизвестные данные. В задаче указывается то, что нужно найти, например, объем или массу другого вещества. Запишите эти данные как неизвестные.
3. Определите формулу. Для решения задач на объем и массу используются различные формулы, которые связывают известные и неизвестные данные. Найдите соответствующую формулу и запишите ее.
4. Подставьте известные данные в формулу и решите уравнение. Произведите подстановку известных значений в формулу и решите получившееся уравнение. Выразите неизвестные данные и найдите их значения.
5. Проверьте ответ. После нахождения ответа проверьте его на правильность. Убедитесь, что ответ имеет смысл с точки зрения условия задачи и единиц измерения.

Следуя этой схеме, вы сможете эффективно решать задачи на объем и массу, используя соответствующие формулы и правильно подставляя значения. Помните, что важно внимательно читать условие задачи и правильно интерпретировать информацию, чтобы успешно решить задачу.

Видео по теме:

Что такое схема в математике?

Схема в математике — это графическое изображение, которое помогает наглядно представить и решить математическую задачу. Она позволяет разложить задачу на отдельные шаги и легче понять ее условие и решение.

Что такое схема в математике?

Схема в математике — это упрощенная графическая модель, которая помогает наглядно представить решение математической задачи. Она состоит из фигур, стрелок, чисел и текста, которые позволяют легче разобраться в условии задачи и ее решении.

Какие задачи можно решать с помощью схемы в математике?

Схема в математике применяется для решения разнообразных задач. Например, с ее помощью можно решить задачу на нахождение площади прямоугольника или треугольника, задачу на нахождение периметра фигуры, задачу на нахождение объема тела и многое другое. Схема позволяет разложить задачу на более простые шаги и легче произвести вычисления.