Объясни по рисунку как составлены каждая схема и каждое равенство математика 1 класс презентация

На презентации представлен рисунок, на котором показаны схемы и равенства из математики для учеников 1 класса. Подробно объясняется, как составлены каждая схема и каждое равенство. Статья содержит наглядные и понятные объяснения, помогающие детям легко усвоить основные понятия математики.

Математика является одним из самых важных предметов в школе. Уже в первом классе дети начинают изучать основы этой науки, включая понятия схем и равенств. Схемы представляют собой графическое изображение математических задач или примеров, что помогает детям визуализировать и легче понять материал.

Равенства играют ключевую роль в математике, поскольку они помогают сравнивать и устанавливать соответствие между различными числами и выражениями. Дети учатся определять равенство и неравенство, а также записывать их с помощью знаков «равно» и «не равно».

В данной статье мы подробно рассмотрим схемы и равенства в математике для первого класса. Мы предоставим простые и понятные объяснения на рисунках, чтобы помочь детям легче усваивать материал и справляться с задачами по данной теме. Мы также предоставим примеры задач, которые помогут закрепить полученные знания и умения.

Математика может показаться сложной на первый взгляд, но с помощью схем и равенств дети смогут более легко вникнуть в эту науку. Мы надеемся, что данная статья поможет ученикам первого класса успешно освоить схемы и равенства в математике и раскрыть свой потенциал в этой области.

Основные понятия

ПонятиеОпределение

Схема	Упорядоченное изображение предметов (чаще всего в виде рисунка), которое помогает наглядно представить математическую задачу или концепцию.
Равенство	Отношение между двумя математическими объектами, которые имеют одинаковую величину или значение.

Эти понятия являются основными для работы с схемами и равенствами в математике. Знание этих определений поможет лучше понять, как использовать схемы и работать с равенствами на уроках математики.

Знаки равенства и неравенства

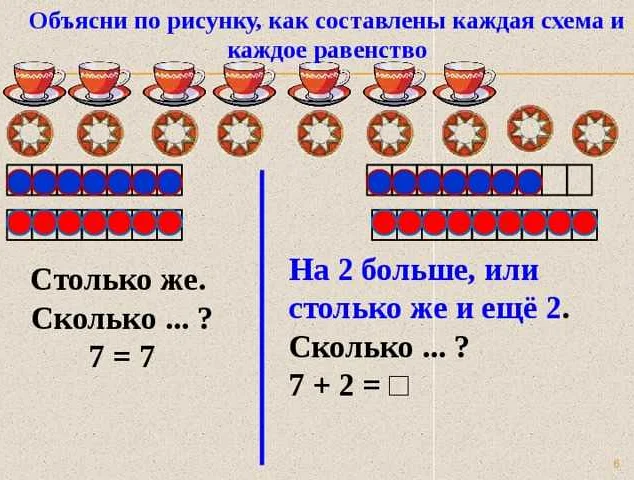
В математике существуют знаки, которые используются для обозначения равенства и неравенства.

Знак равенства (=) используется для того, чтобы указать, что два числа или выражения равны друг другу. Например:

2 + 3 = 5

Это означает, что сумма чисел 2 и 3 равна 5.

Знак неравенства (≠) используется для того, чтобы указать, что два числа или выражения не равны друг другу. Например:

4 + 3 ≠ 7

Это означает, что сумма чисел 4 и 3 не равна 7.

Также существуют знаки для указания отношения больше (>), меньше (

5 > 3

Это означает, что число 5 больше числа 3.

8 < 10

Это означает, что число 8 меньше числа 10.

6 ≥ 5

Это означает, что число 6 больше или равно числу 5.

9 ≤ 11

Это означает, что число 9 меньше или равно числу 11.

Знаки равенства и неравенства используются для сравнения чисел и выражений и играют важную роль в математике.

Примеры схем и равенств на рисунках

В математике, схемы и равенства используются для представления математических отношений и уравнений. Они помогают наглядно показать, как два числа или выражения связаны друг с другом.

Ниже приведены несколько примеров схем и равенств на рисунках:

1. Пример схемы:

a
___
| |
| b |
|___|

В данной схеме переменная «a» представлена горизонтальной чертой, а переменная «b» — вертикальной. Таким образом, схема показывает отношение между этими двумя переменными.

2. Пример равенства:

4 + 3 = 7

В данном равенстве слева от знака равенства расположено выражение «4 + 3», а справа — число «7». Это означает, что сумма чисел 4 и 3 равна 7.

3. Пример равенства с переменными:

x + 2 = 6

В данном равенстве переменная «x» представлена символом «x», а число «2» и «6» — цифрами. Оно означает, что значение переменной «x», при условии что к ней прибавить 2, равно 6.

Схемы и равенства на рисунках помогают детям лучше понять математические концепции и развивают их навыки визуализации и анализа.

Сложение и вычитание в рамках схем

Схемы сложения представляют собой набор объектов, которые нужно сложить. Например, если на схеме изображено 3 яблока и 2 груши, то сумма будет равна 5 фруктам.

Схемы вычитания позволяют визуализировать процесс уменьшения количества объектов. Например, если на схеме изображено 5 яблок, а из них нужно вычесть 2, то останется 3 яблока.

Использование схем в обучении математике помогает детям развить навыки логического мышления, абстрактного мышления и воображения. Кроме того, эта методика помогает улучшить внимание и концентрацию.

Схемы сложения и вычитания в математике 1 класса являются одним из первых шагов в изучении арифметики. Они помогают детям научиться считать и понимать, как выполнять математические операции.

Важно помнить, что схемы не являются единственным методом обучения математике. Они должны использоваться в сочетании с другими методиками, такими как игры, учебные пособия и интерактивные задания.

Умножение и деление в рамках схем

Рассмотрим схему для умножения. Для примера возьмем умножение числа 3 на число 4.

3

x

4

=

12

В этой схеме, число 3 — это множимое, число 4 — это множитель, а результат, число 12 — это произведение.

Теперь рассмотрим схему для деления. Для примера возьмем деление числа 12 на число 4.

12

:

4

=

3

В этой схеме, число 12 — это делимое, число 4 — это делитель, а результат, число 3 — это частное.

С помощью схем мы можем легко представить умножение и деление. Они помогают нам понять, как работают эти операции и как они связаны друг с другом.

Отношение равенства и неравенства к числам

Отношение равенства обозначается символом «=», который ставится между двумя числами. Если два числа равны, то это означает, что они имеют одинаковое значение. Например, 5 = 5.

Отношение неравенства обозначается символами «» (больше) и «<>» (не равно). Если одно число меньше другого, то записывается символ «». Например, 7 > 4. Если два числа не равны, то записывается символ «<>». Например, 2 <> 6.

ОтношениеОбозначениеПример

Равенство	=	5 = 5
Меньше	<	3 < 5
Больше	>	7 > 4
Не равно	<>	2 <> 6

Знание отношений равенства и неравенства к числам помогает в решении различных математических задач и уравнений. Оно также является основой для понимания дальнейших математических понятий и операций.

Вопрос-ответ:

Какие схемы и равенства изучают в 1 классе?

В 1 классе изучаются простейшие математические схемы и равенства. Дети учатся составлять и решать примеры с помощью рисунков и числовых равенств. Например, они могут нарисовать 3 яблока и 2 яблока и записать равенство «3 + 2 = 5».

Зачем изучать схемы и равенства в 1 классе?

Изучение схем и равенств помогает детям развивать математическое мышление и умение решать простейшие задачи. Это также помогает им освоить основы арифметики и логики, что будет полезно в дальнейшем обучении.

Как решать примеры с помощью рисунков?

Для решения примеров с помощью рисунков, дети могут нарисовать предметы, соответствующие числам в примере, и объединить их. Например, для примера «3 + 2», они могут нарисовать 3 яблока и 2 яблока, а затем соединить их вместе, чтобы получить общее количество яблок — 5.

Как записывать равенства в математике 1 класса?

В математике 1 класса равенства записываются с помощью знака равенства (=). Например, равенство «3 + 2 = 5» означает, что сумма 3 и 2 равна 5. Дети учатся читать и записывать такие равенства.

Какие другие математические операции изучают в 1 классе?

В 1 классе помимо сложения, изучают также вычитание и сравнение чисел. Дети учатся вычитать одно число из другого и сравнивать числа: больше, меньше или равны ли они друг другу.

Что такое схемы в математике?

Схемы в математике — это графическое представление математических операций. Они помогают визуализировать процесс решения задач и упрощают понимание математических концепций. На схемах используются различные символы и стрелки, которые показывают последовательность действий.

Как использовать схемы для решения задач в 1 классе?

Для решения задач в 1 классе можно использовать схемы, которые помогут визуализировать процесс решения. Например, для задач на сложение, можно использовать схему с двумя кружками, в которые нужно вписать числа, а затем соединить их стрелкой и написать сумму. Для задач на вычитание можно использовать схему с двумя кружками, из которых один нужно закрасить или вычеркнуть, чтобы показать процесс вычитания.

Практические примеры на равенства и схемы

Пример 1:

У Маши есть 5 яблок, а у Пети — в 2 раза меньше. Какое количество яблок есть у Пети?

Для решения этой задачи, мы можем использовать схему. Пусть количество яблок у Пети будет обозначено буквой «х». Тогда можно записать следующее равенство:

5 = 2 * х

Чтобы найти значение «х», нужно разделить обе части равенства на 2:

х = 5 / 2

Таким образом, у Пети есть 2,5 яблока.

Пример 2:

Андрей бежит со скоростью 8 м/сек. За какое время он пробежит расстояние в 40 метров?

Для решения этой задачи, мы можем использовать схему. Пусть время, за которое Андрей пробежит расстояние, будет обозначено буквой «т». Тогда можно записать следующее равенство:

8 * т = 40

Чтобы найти значение «т», нужно разделить обе части равенства на 8:

т = 40 / 8

Таким образом, Андрей пробежит расстояние в 40 метров за 5 секунд.

Пример 3:

У Алисы есть некоторое количество конфет. Она отдала 3 конфеты своей подруге и у нее осталось вдвое больше, чем у подруги. Сколько конфет было у Алисы?

Для решения этой задачи, мы можем использовать схему. Пусть количество конфет у Алисы будет обозначено буквой «а», а у ее подруги — буквой «п». Тогда можно записать следующее равенство:

а — 3 = 2 * п

Чтобы найти значение «а», нужно прибавить 3 к обеим частям равенства:

а = 2 * п + 3

Таким образом, количество конфет у Алисы было равно двойному количеству конфет у ее подруги плюс 3.

Таким образом, равенства и схемы могут быть использованы для решения практических задач, где нужно найти неизвестное значение, используя известные данные. Это важные инструменты, которые помогают нам логически мыслить и решать математические задачи.

Видео по теме: