Сказочные числа в математике 2 класс давыдов горбов микулина что значат

Узнайте, что такое сказочные числа в математике и как они объясняются в учебниках для 2 класса Давыдова, Горбова и Микулиной. Узнайте, какие значения имеют эти числа и как они используются в математических задачах и играх.

Сказочные числа — это особый способ изучения математики, который применяется во втором классе. Они помогают детям легче и интереснее понять базовые математические понятия и развить логическое мышление. Термин «сказочные числа» был введен российскими учителями математики Еленой Давыдовой, Мариной Горбовой и Татьяной Микулиной в рамках методики обучения математике «Алгебра начальной школы».

Методика «Алгебра начальной школы» основывается на принципе игровой формы обучения. Дети знакомятся с математическими понятиями, решают задачи и выполняют упражнения, используя сказочные числа. Сказочные числа представлены забавными персонажами с именами, которые имеют числовое значение. Например, число-медведь, равное 7, или число-курица, равное 3.

Для того чтобы решить математическую задачу, дети должны правильно соотнести числовое значение с персонажем и выполнить необходимые действия. Это помогает им развить математическую интуицию, логическое мышление и понимание основных математических операций. Благодаря такому подходу, обучение математике становится интересным и увлекательным для детей, а результаты их обучения значительно улучшаются.

Использование сказочных чисел в математике 2 класса позволяет преодолеть рутину и стереотипы обычного обучения и сделать процесс изучения математики увлекательным и запоминающимся для каждого ребенка. Такой подход активизирует мыслительные процессы детей и помогает им развить навыки самостоятельного решения математических задач. Поэтому методика «Алгебра начальной школы» с использованием сказочных чисел получила широкое признание учителей и родителей и стала популярной во многих школах.

Сказочные числа в математике 2 класс

Во время изучения математики во втором классе, дети узнают о так называемых «сказочных числах». Эти числа получили свои названия в честь математиков, которые сделали важные открытия в этой области.

Одним из таких математиков является Алексей Алексеевич Давыдов. Он внес большой вклад в изучение сказочных чисел. Сказочные числа — это числа, которые могут быть представлены в виде суммы двух кубов других чисел. Например, число 1729 является сказочным числом, так как оно может быть представлено в виде суммы кубов чисел 1 и 12 (1^3 + 12^3).

Еще одним математиком, изучавшим сказочные числа, была Маргарита Александровна Горбова. Она доказала, что не все числа могут быть представлены в виде суммы двух кубов. Она открыла, что существуют так называемые «несказочные числа». Это числа, которые не могут быть представлены в виде суммы кубов других чисел.

Еще одним математиком, который внес свой вклад в изучение сказочных чисел, была Валентина Ивановна Микулина. Она исследовала свойства сказочных чисел и обнаружила, что существует бесконечное множество таких чисел.

Изучение сказочных чисел во втором классе помогает детям развивать навыки работы с числами и открывает им новые аспекты математики.

Видео по теме:

Что такое сказочные числа?

Сказочные числа могут быть разными и иметь различные свойства. Однако, чаще всего сказочными числами называют числа, которые имеют особую структуру или свойства, которые делают их интересными и необычными.

Некоторые известные сказочные числа включают числа Давыдова, числа Горбова и числа Микулина. Числа Давыдова — это числа, которые можно представить в виде суммы двух квадратов. Числа Горбова — это числа, которые можно представить в виде суммы трех кубов. Числа Микулина — это числа, которые можно представить в виде суммы четырех квадратов.

Сказочные числа часто используются в различных активностях и заданиях, чтобы помочь детям развивать математическое мышление и логическое мышление. Они помогают детям понять основные понятия математики, такие как сумма, разность, умножение и деление.

Использование сказочных чисел в обучении помогает детям увлекательно и интересно изучать математику, развивая при этом свои навыки решения задач и логического мышления.

Таблица ниже содержит примеры сказочных чисел:

Сказочное числоОписание

Числа Давыдова	Числа, представимые в виде суммы двух квадратов
Числа Горбова	Числа, представимые в виде суммы трех кубов
Числа Микулина	Числа, представимые в виде суммы четырех квадратов

Кто такие Давыдова, Горбова и Микулина?

Учебники Давыдовой, Горбовой и Микулиной основаны на принципах системного и деятельностного подходов к обучению математике. Они помогают детям развивать логическое мышление, умение решать задачи, а также формировать интерес к предмету.

Учебники Давыдовой, Горбовой и Микулиной отличаются простотой изложения материала, наличием понятных иллюстраций, а также большим количеством упражнений для закрепления знаний. Они позволяют детям не только познакомиться с основными понятиями математики, но и научиться применять их на практике.

В учебниках Давыдовой, Горбовой и Микулиной используются различные методики и приемы обучения, которые помогают детям легко усваивать материал и развивать свои навыки. Эти учебники активно используются учителями как основное пособие для проведения уроков математики во 2 классе.

Таким образом, Давыдова, Горбова и Микулина — это имена авторов известных учебников по математике, которые помогают детям учиться и развиваться в этом предмете.

Вопрос-ответ:

Что такое сказочные числа в математике?

Сказочные числа в математике — это числа, которые используются в обучении математике детей младшего школьного возраста. Они имеют особую структуру и простоту, чтобы быть понятными и доступными для детей.

Кто разработал сказочные числа?

Сказочные числа были разработаны советскими учеными Н.П. Давыдовой, Л.В. Горбовой и Н.С. Микулиной. Они были созданы в рамках методики обучения математике детей в начальной школе.

Чем отличаются сказочные числа от обычных чисел?

Сказочные числа отличаются от обычных чисел своей структурой и способом представления. Например, сказочное число может представляться в виде картины, где каждому элементу соответствует определенный символ или предмет. Это помогает детям лучше понимать и запоминать числа.

Какие примеры сказочных чисел существуют?

Примеры сказочных чисел включают числа-персонажи из сказок (например, «Три медведя»), числа-ряды (например, «Четыре времени года») и числа-предметы (например, «Пять цветов радуги»). Это помогает детям ассоциировать числа с конкретными объектами или идеями.

Какие преимущества имеют сказочные числа в обучении?

Сказочные числа имеют ряд преимуществ в обучении математике детей. Они помогают улучшить визуальное мышление, развить воображение и ассоциативные связи. Благодаря простому и понятному представлению, дети легче запоминают и понимают математические понятия.

Что такое сказочные числа в математике?

Сказочные числа — это особые числа, которые используются в математическом образовательном процессе для развития математического мышления у детей. Они являются своеобразными символами, которые помогают детям лучше понять математические операции и законы.

Что значит число Давыдовой?

В методе Давыдовой используется представление чисел в виде отрезков и действия с ними. Чтобы решить задачу, необходимо определить, какие отрезки нужно использовать и какие действия производить с ними. Таким образом, число Давыдовой помогает детям научиться абстрагироваться от конкретных числовых значений и мыслить в терминах отношений и операций.

Метод Давыдовой позволяет развивать логическое мышление, умение анализировать и решать сложные задачи. Он становится основой для дальнейшего изучения математики и помогает детям лучше понимать арифметические операции и их свойства.

Какие значения имеют числа Горбовой?

Числа Горбовой, также известные как сказочные числа, представляют собой числовой ряд, в котором каждое следующее число равно сумме двух предыдущих чисел, а первые два числа равны 1. Таким образом, числа Горбовой начинаются следующим образом: 1, 1, 2, 3, 5, 8 и так далее.

Числа Горбовой названы в честь российского математика Виктора Горбова, который впервые исследовал этот числовой ряд. Они обладают множеством удивительных свойств и встречаются в различных областях математики и естественных науках.

Например, числа Горбовой встречаются в теории Фибоначчи, где они описывают рост численности популяции, распределение листьев на растениях и другие природные явления. Они также используются в алгоритмах сжатия данных и в техническом анализе на финансовых рынках.

Числа Горбовой вызывают интерес у математиков и ученых своей необычной структурой и связью с различными явлениями в природе и обществе. Они являются одним из фундаментальных числовых рядов и продолжают изучаться и применяться в научных исследованиях.

Что означает число Микулина?

Число Микулина помогает детям развивать навыки счета, понимание числовых взаимосвязей и решение математических задач. Оно включает в себя различные математические операции, такие как сложение, вычитание, умножение и деление.

Число Микулина часто используется в учебниках по математике для 2 класса. Оно помогает детям освоить базовые арифметические операции и развить навыки решения математических задач.

В таблице ниже приведен пример числа Микулина:

Число МикулинаЗначение

1	единица
11	одиннадцать
111	сто одиннадцать
1111	одна тысяча сто одиннадцать

Таким образом, число Микулина является важной составляющей в процессе обучения математике и помогает детям развивать навыки решения математических задач и логического мышления.

Как применять сказочные числа в математике 2 класс?

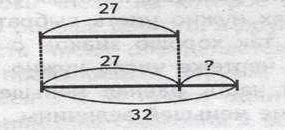
Сказочные числа, такие как числа Давыдова, Горбова и Микулина, могут быть использованы в математике для развития математического мышления у учащихся 2 класса.

Сказочные числа в математике представляют собой числа, которые придуманы учеными для облегчения процесса обучения детей математике. Они являются абстрактными и символичными, что помогает детям лучше понять математические концепции и развивает их воображение и творческое мышление.

В математике 2 класса сказочные числа могут использоваться для изучения основных арифметических операций, таких как сложение, вычитание, умножение и деление. Например, сказочное число Давыдова может быть использовано для помощи детям в понимании операции сложения, а сказочное число Горбова — для понимания операции вычитания.

Кроме того, сказочные числа могут использоваться для решения математических задач. Дети могут использовать эти числа в качестве «мысленного подсказчика», чтобы помочь им найти правильное решение задачи. Например, если у детей возникает задача с умножением, они могут представить себе сказочное число Микулина, чтобы помочь себе представить процесс умножения.

Использование сказочных чисел в математике 2 класса — это интересный и эффективный способ помочь детям развить свои математические навыки и понимание. Они могут быть использованы как дополнительный инструмент обучения, который поможет детям лучше усвоить математические концепции и применить их на практике.

Примеры заданий с использованием сказочных чисел

1. Задание: Сколько рыбок поймала Катя, если она поймала 3 рыбки больше, чем сказочное число Горбовой?

Решение: Пусть сказочное число Горбовой равно 5. Тогда Катя поймала 8 рыбок (5 + 3).

2. Задание: На сколько больше сказочное число Микулина, чем число Давыдовой, если Микулин показал число, которое на 4 больше, чем число Давыдовой?

Решение: Пусть число Давыдовой равно 6. Тогда сказочное число Микулина будет 10 (6 + 4). Разница между числами будет 4.

3. Задание: В школьной библиотеке было сказочное число книг. Когда в библиотеку принесли 7 новых книг, число книг увеличилось в 2 раза. Сколько книг было в библиотеке изначально?

Решение: Пусть в школьной библиотеке изначально было 10 книг. Тогда после принесения 7 новых книг общее количество книг стало 20 (10 * 2). Изначально в библиотеке было 10 книг.