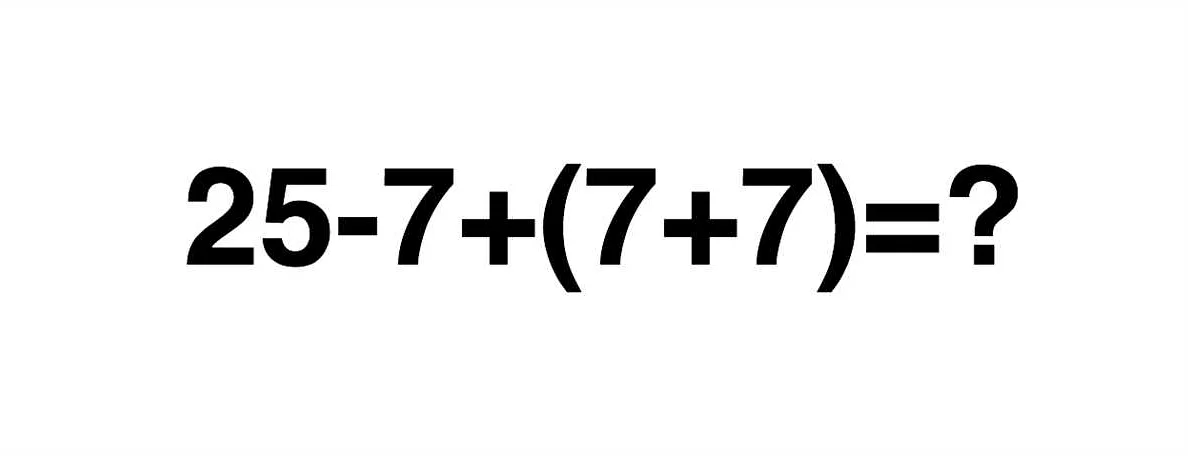Сколько уроков математики нужно, чтобы хорошо сдать экзамен?

Статья рассказывает о том, сколько времени нужно уделять математике, чтобы стать хорошим специалистом в этой области. Изучение математики требует усилий и терпения, но результаты впечатляют. Читайте нашу статью и узнайте, сколько будет математика для вас!

Математика — это неотъемлемая часть нашей жизни. Эта наука помогает нам решать сложные задачи и принимать важные решения. Люди изучали математику с древности и до сих пор продолжают открывать новые ее аспекты.

В данной статье мы рассмотрим основные принципы связанные с расчетами и примерами в математике. Мы познакомимся с основными операциями, математическими формулами и простыми примерами для понимания. Вы узнаете, как правильно решать задачи и расчитывать различные величины.

Чтобы успешно использовать математику в повседневной жизни, необходимо иметь хорошее понимание основных математических принципов. Эта статья поможет вам обрести этот навык, чтобы вы могли применять математику эффективно в любого типа задачах.

Математика: зачем ее изучать?

Математика является одним из самых важных предметов в школьной программе. Она не только помогает развивать логическое мышление, но и является основой для многих других наук, включая физику, химию и инженерию.

Кроме того, математика применяется в повседневной жизни. Знания в области математики необходимы для решения задач в бизнесе, финансах, налоговой системе и других областях жизни.

Изучение математики помогает развивать умение анализировать, сравнивать и делать выводы на основе числовых данных. Эти навыки являются необходимыми для принятия правильных решений в различных сферах жизни.

Кроме того, изучение математики помогает развивать творческий подход к решению задач. Существует множество способов решения одной и той же задачи, и знание математики позволяет выбрать самый оптимальный и эффективный подход.

Таким образом, изучение математики не только является важным предметом в школьной программе, но и абсолютно необходимым для успешной жизни и карьеры. Хотя математика может показаться сложной и утомительной, ее изучение открывает множество возможностей и способствует развитию важных навыков.

Видео по теме:

Что такое числа и как их считать

Числа – это математические объекты, которые используются для измерения количества, размеров, расстояний, времени и т.д. Каждое число имеет свою уникальную числовую величину и представляется цифрами. Числа могут быть целыми или дробными.

Существует множество методов для считывания и записи чисел. Один из самых простых и распространенных методов – это десятичная система счисления. В этой системе каждая цифра записывается с помощью 10 возможных символов (от 0 до 9), а каждая цифра запиcывается в соответствующем разряде в зависимости от ее значения. Например, число 1256 состоит из четырех цифр и записывается следующим образом:

• 1 в тысячных разряде (10^3)
• 2 в сотых разряде (10^2)
• 5 в десятичном разряде (10^1)
• 6 в единичном разряде (10^0)

Для проведения арифметических операций с числами используются основные математические операции: сложение, вычитание, умножение и деление. Кроме того, для упрощения работы с большими числами используются различные методы округления, аппроксимации и т.д.

Важно помнить, что числа играют важную роль в различных областях жизни, от наук до повседневных задач. Умение считывать и работать с числами открывает множество возможностей и является необходимым навыком для любого человека.

Арифметические действия и их приоритет

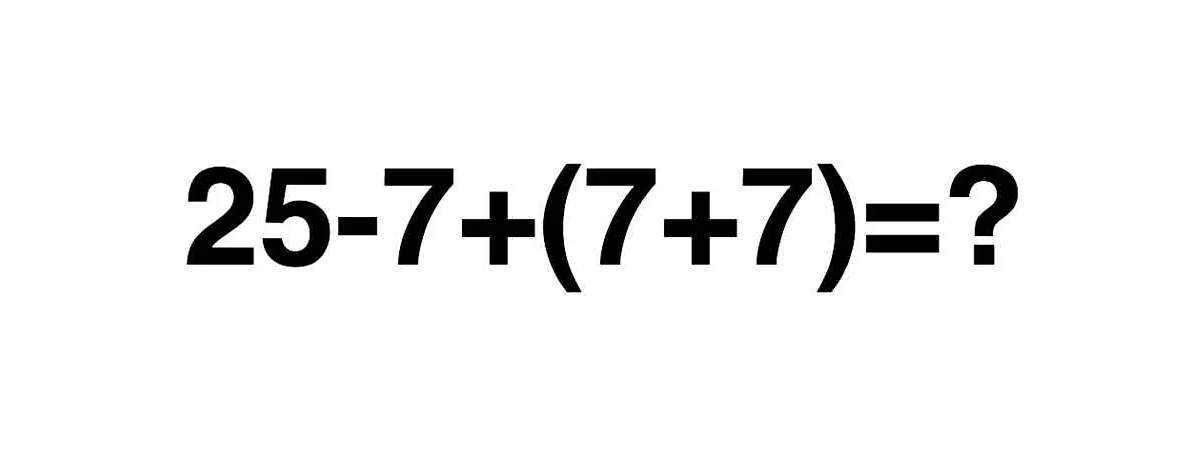
В математике существует несколько арифметических действий, каждому из которых присвоен свой приоритет.

1. Скобки — имеют наивысший приоритет. Если в выражении есть скобки, то они выполняются первыми.
2. Умножение и деление — выполняются вторыми по приоритету.
3. Сложение и вычитание — имеют наименьший приоритет. Они выполняются последними, после всех предыдущих действий.

Если в выражении есть несколько действий с одинаковым приоритетом, то они выполняются слева направо.

Например, в выражении 2 + 3 * 4 каждый операнд умножения имеет более высокий приоритет, чем операция сложения. Таким образом, сначала нужно выполнить действие 3 * 4, а затем прибавить к результату 2. Итоговым ответом будет 14.

Знание приоритетов арифметических действий позволит вам правильно выполнять математические выражения и избежать ошибок в расчетах.

Как решать уравнения и неравенства

Уравнения и неравенства — это основные математические объекты, которые часто встречаются в решении домашних заданий и тестах. Они могут быть простыми или сложными, но есть несколько общих правил, которые помогут вам решить их правильно.

Первый шаг при решении уравнения или неравенства — это упрощение выражений, если это возможно. Сложите или вычтите числа на обеих сторонах уравнения, чтобы избавиться от постоянных членов. Умножьте или поделите обе стороны на одно и то же число, чтобы избавиться от переменных в знаменателе.

Если вы не можете упростить выражение, то перенесите все переменные на одну сторону уравнения, вынесите их за скобку и сверните числа в одно. Затем разделите на коэффициент при переменной х. Полученный результат будет корнем уравнения.

При решении неравенств важно знать знаки неравенства и правила их изменения. Если вы умножаете или делите обе стороны неравенства на отрицательное число, то нужно помнить, что знак неравенства изменится.

• Для уравнений нужно найти точное значение переменной, которое удовлетворяет условию.
• Для неравенств нужно найти диапазон значений переменной, которые удовлетворяют условию.

При решении сложных уравнений и неравенств часто нужно использовать таблицы или графики, чтобы найти все возможные значения переменной. Не забывайте о том, что правильное решение должно быть проверено.

Геометрия: фигуры и их свойства

Геометрия – это наука, изучающая пространственные формы и их свойства. Она играет важную роль в математике, а также во многих научных и технических областях.

Среди основных геометрических фигур можно выделить точку, линию, отрезок, угол, треугольник, квадрат, прямоугольник, круг и многие другие. Каждая из этих фигур обладает своими характерными свойствами, которые могут быть использованы для решения различных геометрических задач.

Например, круг – это фигура, состоящая из всех точек, находящихся на одинаковом расстоянии от центра. Его радиус – это расстояние от центра до любой точки на окружности. Площадь круга можно вычислить по формуле S=πr², где π – это число пи, а r – радиус круга.

• Треугольник – это фигура, состоящая из трех отрезков, соединяющих три точки. Он обладает свойствами, такими как сумма углов треугольника равна 180 градусам, а высота – перпендикуляр, проведенный из вершины к основанию, делит треугольник на две равные по площади части.
• Прямоугольник – это фигура, обладающая четырьмя прямыми углами и противоположными сторонами, равными по длине. Площадь прямоугольника можно найти, умножив длину на ширину.
• Квадрат – это фигура, имеющая четыре прямых угла и стороны равные между собой. Площадь квадрата можно найти по формуле S=a², где a – длина стороны.

Знание геометрии на практике помогает решать многие задачи, связанные с различными областями жизни, такими как архитектура, механика, машиностроение и т.д. Поэтому овладение базовыми знаниями этой науки является важным компонентом математической грамотности.

Площади и объемы: формулы и расчеты

Площадь круга вычисляется по формуле S=πr², где π≈3.14, r — радиус круга. Например, если радиус круга равен 5 см, то площадь круга будет S=3.14*5*5= 78.5 см².

Площадь треугольника можно вычислить по формуле S=1/2ah, где а — основание треугольника, h — высота. Например, если основание треугольника равно 10 см, а высота равна 5 см, то площадь треугольника будет S=1/2*10*5=25 см².

Объем куба можно найти, умножив длину, ширину и высоту куба. Например, если куб имеет длину, ширину и высоту 5 см, то его объем будет V=5*5*5= 125 см³.

Объем цилиндра можно вычислить по формуле V=πr²h, где r — радиус основания цилиндра, h — высота цилиндра. Например, если радиус основания цилиндра равен 4 см, а высота равна 10 см, то объем цилиндра будет V=3.14*4²*10=502.4 см³.

• Помните, что для вычислений требуется правильно определить единицы измерения.
• Формулы и расчеты могут использоваться во многих сферах жизни, от строительства до решения ежедневных задач.
• При написании программного кода часто требуется выполнить математические операции, поэтому понимание и знание формул математики — важный навык.

Тригонометрия: расчет углов и сторон треугольника

Тригонометрия — раздел математики, который изучает связь между углами и сторонами треугольника. С помощью тригонометрии можно рассчитать длину стороны треугольника, если известны длины других сторон и углы между ними, или найти значение угла, зная длины сторон. Одним из основных понятий тригонометрии являются тригонометрические функции.

Существует шесть тригонометрических функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Они вычисляются для заданного угла в прямоугольном треугольнике. Синус угла равен отношению противолежащей стороны к гипотенузе, косинус угла — отношению прилежащей стороны к гипотенузе, а тангенс — отношению противолежащей стороны к прилежащей стороне.

Для расчета углов и сторон треугольника можно использовать таблицу трехгранных тригонометрических функций или специальный калькулятор. С помощью тригонометрии можно решать множество задач, например, находить высоту треугольника, расстояние до объекта, угол между двумя объектами и многое другое.

Знание тригонометрии полезно не только для математических расчетов, но и для решения задач в различных областях науки и техники, таких как физика, инженерия, радиотехника и другие.

Математика в жизни: расчеты и применение

Математика является неотъемлемой частью нашей жизни. Она помогает нам в решении различных проблем и задач, связанных с ежедневной жизнью. Используя математические знания, мы можем рассчитать различные параметры в жизни, такие как расстояния, скорость, время, объем или площадь.

В быту, математика может помочь в решении задач, связанных с финансами, таких как расчет налогов и бюджетирование домашних расходов. Также, она может использоваться для расчета необходимых ингредиентов для приготовления еды или расчета необходимого времени для выпекания теста.

В производстве, математика используется для расчета производственных процессов, планирования и оптимизации производства, а также в качестве инструмента при анализе экономической деятельности предприятия.

Кроме того, математика играет большую роль в науке. Она представляет основу для многих научных открытий и достижений. Она используется в различных областях, таких как физика, химия, биология, астрономия, экономика и много других.

Короче говоря, математика необходима для нас для того, чтобы продвигаться вперед, решать сложные задачи и принимать взвешенные решения. Важно также понимать, что математика не является только учением, а является частью жизни, которая помогает нам добиваться успеха в различных сферах деятельности.

Применение математики в науке и технике

Математика является фундаментальной наукой, служащей основой для других наук и технологий. Ее важность для науки и техники трудно переоценить, ведь многие принципы и законы, которые используются в современных технологиях и научных исследованиях, основываются на математических выкладках и расчетах.

Одним из примеров применения математики в технике является проектирование и разработка компьютерных игр, где необходимо решать задачи связанные с графикой, физикой, искусственным интеллектом и другими математическими принципами.

Кроме того, математические методы используются в технике для проектирования новых материалов и конструкций, создания и оптимизации логистических систем, а также для моделирования и прогнозирования различных явлений в физике и других областях науки.

Также математика является неотъемлемой частью научных исследований, позволяя установить связь между различными величинами и провести качественный и количественный анализ данных. Без использования математических методов и правил проведения расчетов, многие научные исследования были бы невозможными.

• Итак, применение математики в науке и технике на сегодняшний день очень важно и актуально;
• Математика помогает разрабатывать новые технологии и конструкции, производить расчеты и моделирование, а также проводить анализ данных;
• Без математики многие научные и технические достижения были бы невозможными.

Основные ошибки в расчетах и как их избежать

1. Неправильная интерпретация условий задачи

Одной из первых и основных ошибок при решении математических задач является неправильная интерпретация условий задачи. Перед началом решения необходимо внимательно прочитать формулировку, выделить ключевые слова и построить схему.

2. Ошибки при переносе и расстановке знаков

При выполнении расчетов часто возникают ошибки при переносе и расстановке знаков. Например, при раскрытии скобок может быть пропущен знак >, а при выполнении операции умножения или деления — знак > или >.

3. Неверная выбор единиц измерения

Одна из распространенных ошибок при решении задач, связанных с физическими величинами, — неверный выбор единиц измерения. Нужно учитывать, что единицы измерения могут быть разными и выполнять соответствующие преобразования.

4. Пропуск необходимых вычислений

При выполнении сложных вычислений очень легко пропустить необходимый шаг. Чтобы этого не происходило, рекомендуется на каждом шаге проверять правильность полученного результата и сверяться со схемой или формулой.

5. Использование неправильной формулы

В математике существует множество формул и правил, каждое из которых применяется в разных ситуациях. Важно правильно идентифицировать задачу и выбрать нужную формулу.

Избежать этих ошибок поможет внимательное изучение условий задачи, тщательное выполнение расчетов и применение соответствующих формул и правил.

Как изучать математику: советы и ресурсы

Математика – это один из наиболее важных предметов, на знаниях которого строится многие сферы деятельности. Изучать математику может быть сложно, но с помощью соответствующих подходов и ресурсов это может стать интересным и увлекательным процессом. Ниже представлены несколько советов и ресурсов, которые помогут вам в изучении математики.

Советы по изучению математики

• Постройте твердый фундамент: Для изучения математики важно иметь отличные знания арифметики, алгебры и геометрии. Убедитесь, что вы понимаете основы, прежде чем переходить к более сложным концепциям.
• Распланируйте время: Изучение математики требует много времени и труда. Распределяйте свое время между учебными занятиями, самостоятельной работой и отдыхом.
• Решайте много задач: Решение задач – это лучший способ понимания математических концепций. Решите как можно больше задач, особенно тех, которые вызывают трудности.
• Ищите помощь: Если вы столкнулись с трудностями, не стесняйтесь обращаться за помощью у учителей, родителей или одноклассников. Возможно, вам понадобится дополнительное объяснение или просто кто-то, кто поможет вам преодолеть трудности.
• Изучайте различные подходы: Есть много способов, которыми можно изучать математику. Используйте различные подходы, чтобы увидеть, что работает для вас.

Ресурсы для изучения математики

Книги: Существует множество книг, которые могут помочь в изучении математики. Выберите книгу, которая наиболее подходит для вашего уровня и учебной программы.

Видеоуроки: Видеоуроки – это отличный способ для вас, чтобы получить разъяснение сложных концепций. Проверьте популярные видео-уроки на YouTube или в других источниках.

Математические игры: Игры, связанные с математикой, могут быть веселым и эффективным способом, чтобы улучшить навыки. Многие из них доступны онлайн.

Онлайн-платформы для изучения математики: Существует множество онлайн-платформ, которые помогут вам изучать математику. Некоторые из них предлагают бесплатный доступ, а некоторые – платные курсы.

РесурсСтоимостьФормат

Khan Academy	Бесплатно	Видеоуроки и задания
Coursera	Платно и бесплатно	Онлайн-курсы
Udemy	Платно и бесплатно	Онлайн-курсы

Вопрос-ответ:

Что такое математика?

Математика — наука о числах, количествах и пространственных отношениях. Она изучает правила и законы, которым подчиняются эти объекты, а также разрабатывает методы работы с ними.

Какие виды математики существуют?

Существует множество разных видов математики, например: алгебра, геометрия, теория вероятностей, математическая статистика, теория чисел, математическая логика, математическая физика и т.д.

Зачем нужна математика в нашей жизни?

Математика играет очень большую роль в нашей жизни, она помогает нам решать различные задачи, делать точные вычисления, понимать и анализировать статистические данные, работать с компьютерами, проектировать и строить здания и многое другое.

Какие математические примеры существуют?

Существует множество разных математических примеров, например: сложение, вычитание, умножение, деление чисел; решение уравнений и систем уравнений; вычисление площадей и объемов фигур; расчет процентов и т.д.

Как правильно решать математические задачи?

Для решения математических задач необходимо следовать определенному алгоритму. Он включает в себя такие шаги, как: чтение задачи, выделение ключевых данных, выбор подходящего метода решения, проведение необходимых вычислений, проверка ответа.

Какие ошибки часто допускаются при выполнении математических операций?

Часто допускаются такие ошибки, как: неправильное чтение условия задачи, неверный выбор метода решения, опечатки при записи чисел, невнимательность того, кто решает задачу. Поэтому важно следить за точностью и внимательностью при выполнении математических операций.

Могу ли я научиться решать математические задачи, если мне трудно понимать математику?

Да, конечно. Хорошее понимание математики приходит с опытом и практикой. Чтобы научиться решать математические задачи, необходимо выполнять их много раз, учиться выбирать подходящий метод решения, а также получать знания и советы от более опытных людей.