Сколько чисел в математике
Содержимое
- 1 Сколько чисел в математике
- 1.1 Основные виды чисел
- 1.2 Натуральные числа: определение и свойства
- 1.3 Целые числа: отрицательные и положительные
- 1.4 Рациональные числа: дроби и их свойства
- 1.5 Иррациональные числа: корни и число π
- 1.6 Вещественные числа: десятичные дроби и числа с бесконечной десятичной частью
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Комплексные числа: мнимая единица и алгебраическая форма
- 1.10 Бесконечность в математике: пределы и бесконечно малые числа
В математике бесконечное количество чисел, которые можно разделить на различные категории, такие как натуральные, целые, рациональные и иррациональные числа. Узнайте, сколько всего чисел существует в мире математики и какие особенности имеют разные типы чисел.
Математика – это наука, изучающая числа. Но сколько же существует чисел в математике? Ответ на этот вопрос не так прост, как может показаться на первый взгляд. В математике существует множество различных видов чисел, каждый из которых имеет свои особенности. Некоторые из них мы изучаем еще в школе, а другие – только на уровне высшей математики.
Начнем с основных видов чисел. Все мы знакомы с натуральными числами, которые используются для подсчета предметов и различных объектов. К натуральным числам добавляют ноль и получают так называемые целые числа. Они включают в себя как положительные, так и отрицательные числа.
Однако натуральные и целые числа недостаточно для решения всех математических задач. Для этого были введены рациональные числа – числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа включают в себя как обыкновенные дроби, так и десятичные дроби.
«Но существуют ли числа, которые нельзя представить в виде дроби?» – может возникнуть вопрос. Да, такие числа действительно существуют. Их называют иррациональными числами. Иррациональные числа не могут быть представлены в виде дроби и имеют бесконечное количество десятичных знаков после запятой. Примерами иррациональных чисел являются числа π (пи) и √2 (корень из двух).
Таким образом, в математике существуют четыре основных вида чисел: натуральные, целые, рациональные и иррациональные. Но это не все – в математике также есть комплексные числа, которые состоят из действительной части и мнимой части. Комплексные числа играют важную роль в алгебре и имеют множество приложений в физике и других областях науки.
И наконец, стоит упомянуть о бесконечности в математике. Бесконечность – это понятие, которое означает отсутствие конца или границы. В математике есть различные виды бесконечности, такие как счетная и несчетная бесконечность. Бесконечность используется для описания таких понятий, как бесконечно малые и бесконечно большие числа, а также для решения различных математических задач.
Основные виды чисел

В математике существует множество различных видов чисел, каждый из которых имеет свои особенности и применяется в конкретных областях.
Одним из основных видов чисел являются натуральные числа. Это числа, которые используются для обозначения количества элементов в конечных множествах. Натуральные числа обычно обозначаются символом N и включают в себя числа от 1 до бесконечности.
Другим важным видом чисел являются целые числа. Они включают в себя все натуральные числа, а также их отрицательные значения и ноль. Целые числа обозначаются символом Z.
Рациональные числа – это числа, которые могут быть представлены в виде обыкновенной или десятичной дроби. Они включают в себя все целые числа, а также десятичные дроби с конечным или периодическим числом знаков после запятой. Рациональные числа обозначаются символом Q.
Вещественные числа включают в себя все рациональные числа, а также иррациональные числа, которые не могут быть представлены в виде обыкновенной или десятичной дроби. Такие числа, как корень квадратный из двух (≈ 1,4142) или число π (≈ 3,1416), являются иррациональными. Вещественные числа обозначаются символом R.
Комплексные числа – это числа, которые состоят из двух частей: действительной и мнимой. Они обозначаются символом С и имеют вид a + bi, где a и b – действительные числа, а i – мнимая единица, которая определяется как √(-1).
Это лишь некоторые из основных видов чисел, которые используются в математике. Каждый из них имеет свои уникальные свойства и применяется в различных областях науки и техники.
Натуральные числа: определение и свойства

Основные свойства натуральных чисел:
- Натуральные числа не могут быть отрицательными или дробными.
- Между любыми двумя натуральными числами всегда можно найти бесконечное количество других натуральных чисел.
- Натуральные числа можно складывать, вычитать, умножать и делить, получая другие натуральные числа.
- У натуральных чисел есть порядок: каждое число имеет свое следующее число и предыдущее число.
Натуральные числа играют важную роль в математике и употребляются в различных областях науки и повседневной жизни.
Целые числа: отрицательные и положительные

В математике целыми числами называются все положительные и отрицательные числа, а также нуль. Целые числа обозначаются символом Z.
Положительные целые числа — это числа, которые больше нуля. Они обозначаются символом Z+ или Z*. Например, 1, 2, 3, 100 — все они являются положительными целыми числами.
Отрицательные целые числа — это числа, которые меньше нуля. Они обозначаются символом Z-. Например, -1, -2, -3, -100 — все они являются отрицательными целыми числами.
Нуль, обозначаемый символом 0, является особым целым числом. Он не является ни положительным, ни отрицательным числом, но входит в множество целых чисел.
Целые числа имеют ряд свойств, которые позволяют производить с ними различные математические операции, как например, сложение, вычитание, умножение и деление.
Целые числа играют важную роль в математике и находят применение во многих областях, таких как физика, экономика, информатика и т. д.
Рациональные числа: дроби и их свойства

Дробь — это математический объект, который представляет собой отношение двух чисел: числителя и знаменателя. Числитель обозначает количество частей, которые мы имеем, а знаменатель обозначает количество частей, на которые мы разделили целое число или объект.
Рациональные числа обладают рядом свойств:
СвойствоОписание
| Замкнутость относительно сложения и умножения | Сумма или произведение двух рациональных чисел также является рациональным числом. |
| Существование обратного элемента | У каждого ненулевого рационального числа существует обратное число, которое при умножении на него дает единицу. |
| Существование нейтрального элемента | Рациональное число 1 является нейтральным элементом относительно умножения, а число 0 — относительно сложения. |
| Возможность сокращения | Рациональное число можно представить в виде дроби с наименьшими целыми числами числителя и знаменателя. |
Рациональные числа имеют важное значение в математике и находят применение в различных областях, включая физику, экономику и информатику.
Иррациональные числа: корни и число π

Одним из основных видов иррациональных чисел являются числа-корни. Например, квадратный корень из двух (√2) является иррациональным числом. Это означает, что √2 не может быть точно представлено в виде десятичной дроби или дроби. Значение √2 приближенно равно 1.41421356…
Другим примером иррационального числа является число π (пи). Число π является отношением длины окружности к ее диаметру. Значение числа π приближенно равно 3.14159265… и оно также не может быть точно представлено в виде десятичной дроби или дроби.
Иррациональные числа играют важную роль в математике и широко используются в различных областях, таких как физика, инженерия и компьютерные науки.
Вещественные числа: десятичные дроби и числа с бесконечной десятичной частью
Десятичные дроби представляют собой числа, у которых десятичная часть записана после запятой. Например, число 3,14 является десятичной дробью, где 3 — целая часть, а 14 — десятичная часть.
Числа с бесконечной десятичной частью могут быть представлены в виде бесконечных десятичных дробей или периодических десятичных дробей. Бесконечные десятичные дроби не имеют периода и продолжаются в бесконечность. Например, число π (пи) — это бесконечная десятичная дробь, начинающаяся с 3,14159265358979323846 и продолжающаяся в бесконечность.
Периодические десятичные дроби имеют повторяющийся блок цифр, который периодически повторяется. Например, число 1/3 (одна треть) равно 0,3333…, где 3 бесконечно повторяется.
Для удобства записи и использования вещественных чисел, в математике используется система позиционной нумерации с основанием 10. В этой системе каждая цифра в позиционной записи числа имеет вес, зависящий от позиции цифры. Например, в числе 123,4 цифра 1 имеет вес 100, цифра 2 имеет вес 10, цифра 3 имеет вес 1, а цифра 4 имеет вес 0,1.
Вещественные числа имеют большой диапазон значений, включая как очень маленькие числа (например, 0,00000001), так и очень большие числа (например, 1000000000). Они играют важную роль в науке, технике и ежедневной жизни, где используются для измерений, вычислений и представления дробных значений.
Тип вещественного числаПример
| Десятичная дробь | 3,14 |
| Бесконечная десятичная дробь | π (пи) = 3,14159265358979323846… |
| Периодическая десятичная дробь | 1/3 = 0,3333… |
Вещественные числа являются важной частью математической теории и имеют множество приложений в различных областях знания.
Видео по теме:
Вопрос-ответ:
Сколько основных видов чисел есть в математике?
В математике существует несколько основных видов чисел: натуральные числа (1, 2, 3 и так далее), целые числа (включая нуль и отрицательные числа), рациональные числа (числа, которые можно представить в виде дроби), иррациональные числа (числа, которые не могут быть представлены в виде дроби) и комплексные числа (сумма вещественной и мнимой части).
Какова бесконечность в математике?
Бесконечность в математике — это концепция, описывающая отсутствие границы или ограничений. В математике существует несколько типов бесконечности, таких как счетная бесконечность (количество натуральных чисел), континуальная бесконечность (количество вещественных чисел) и другие.
Какие числа считаются натуральными?
Натуральные числа — это положительные целые числа, начиная с 1 и продолжая до бесконечности. Включается 0 в натуральные числа в зависимости от определения. Некоторые математики включают 0 в натуральные числа, а некоторые нет.
Какие числа считаются рациональными?
Рациональные числа — это числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами. Например, 1/2, 3/4, -2/5 — все это рациональные числа. Рациональные числа включают как целые числа, так и десятичные дроби.
Какие числа считаются иррациональными?
Иррациональные числа — это числа, которые не могут быть представлены в виде дроби и не являются рациональными. Они имеют бесконечное количество недвигающихся цифр после запятой. Например, корень из 2, число π (пи) и е (основание натурального логарифма) — все это иррациональные числа.
Какие основные виды чисел существуют в математике?
В математике существуют различные виды чисел, такие как натуральные числа, целые числа, рациональные числа, иррациональные числа и комплексные числа.
Комплексные числа: мнимая единица и алгебраическая форма

Мнимая единица — это число, которое обладает свойством i^2 = -1. Она является основным элементом в комплексных числах и позволяет выполнять операции, которые невозможны при использовании только вещественных чисел. Например, корень из отрицательного числа.
Комплексные числа могут быть представлены в алгебраической форме, которая выражается в виде a + bi. В алгебраической форме a представляет вещественную часть комплексного числа, а b — мнимую часть. Алгебраическая форма позволяет удобно выполнять операции с комплексными числами, такие как сложение, вычитание, умножение и деление.
Комплексные числа широко применяются в различных областях математики, физики и инженерии. Они находят применение в решении уравнений, моделировании электрических цепей, анализе колебаний и многих других задачах.
Бесконечность в математике: пределы и бесконечно малые числа
Пределы — это концепция, которая позволяет определить поведение функции или последовательности при приближении к определенной точке. Предел функции описывает, как значение функции изменяется при приближении аргумента к определенной точке. Предел последовательности определяет, как значения элементов последовательности стремятся к определенному числу при увеличении их индексов.
Бесконечно малые числа — это числа, которые стремятся к нулю, но не достигают его. Они играют важную роль в анализе и дифференциальных уравнениях. Бесконечно малые числа позволяют приближенно описывать изменение функций в близкой окрестности точки.
Однако бесконечность и бесконечно малые числа требуют осторожного обращения. Они не являются обычными числами и не подчиняются обычным арифметическим операциям. В математике существует строгий формализм для работы с бесконечностью, который позволяет избежать ошибок и противоречий.
В заключение, бесконечность, пределы и бесконечно малые числа являются важными инструментами в математике. Они позволяют анализировать и описывать сложные явления и процессы, связанные с изменением функций и последовательностей. Понимание этих концепций помогает строить более точные модели и решать разнообразные задачи в математике и ее приложениях.



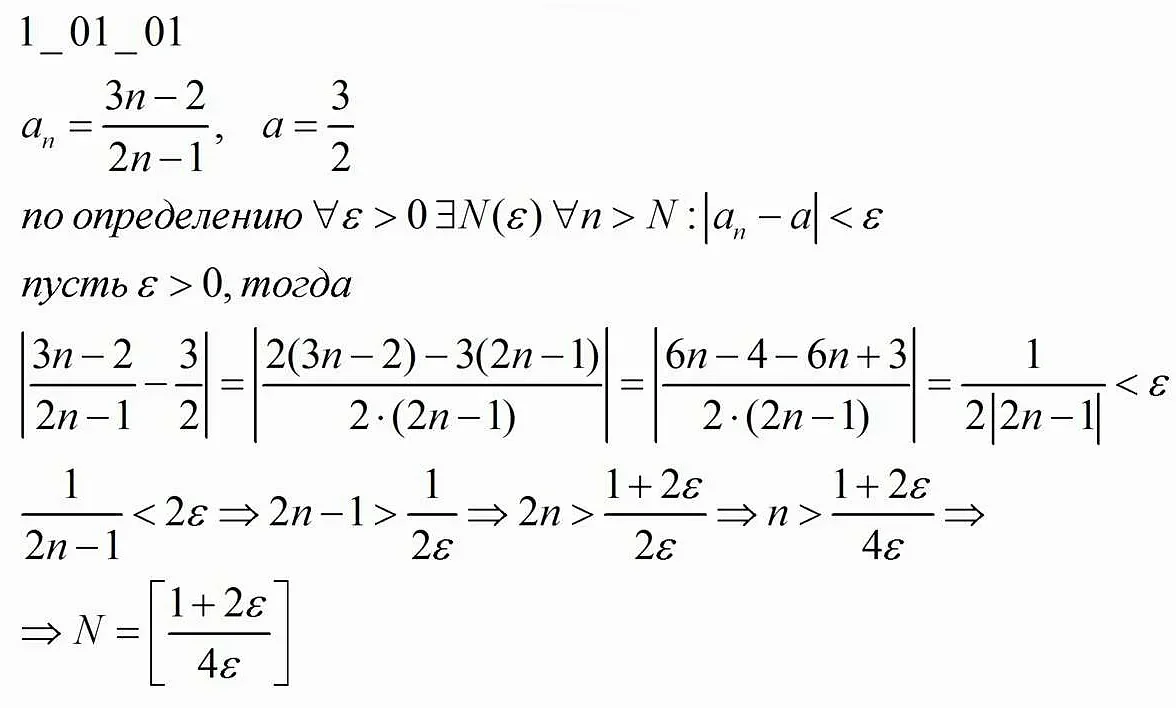
Статья очень интересная и познавательная! Я всегда задумывался, сколько чисел существует в математике. Оказывается, их бесконечное множество! Я знал о натуральных числах, целых числах, рациональных числах и действительных числах, но оказывается, есть еще и мнимые числа, комплексные числа и дроби. Это так удивительно! Статья хорошо объясняет каждый вид чисел и даёт примеры их использования. Я теперь понимаю, что все эти виды чисел необходимы в разных областях математики и физики. Особенно заинтересовали меня комплексные числа, которые имеют мнимую единицу i. Теперь мне интересно узнать, как они применяются в реальной жизни. Также статья затрагивает тему бесконечности чисел. Меня всегда поражало, что число Пи и число Эйлера являются бесконечными и иррациональными. Но оказывается, что существуют еще и бесконечные последовательности чисел, такие как геометрическая прогрессия или ряды. Это действительно интересно и открывает новые горизонты в понимании математики. В целом, статья очень познавательная и доступно объясняет сложные концепции математики. Я рад, что я ее прочитал и узнал много нового о числах. Теперь я с нетерпением жду новых статей на эту тему!